Cho hàm số y Chứng minh rằng hàm số đã cho luôn có cực đại, cực tiểu với mọi m lớn hơn 0

Giải sách bài tập Toán 12 Bài tập cuối chương 1 - Kết nối tri thức

Bài 1.66 trang 36 SBT Toán 12 Tập 1: Cho hàm số $y = \frac{m x^{2} + (2 m - 1) x - 1}{x + 2}$ với m là tham số.

a) Chứng minh rằng hàm số đã cho luôn có cực đại, cực tiểu với mọi m > 0.

b) Khảo sát và vẽ đồ thị (H) của hàm số đã cho với m = 1.

c) Giả sử ∆ cắt tiệm cận đứng và tiệm cận xiên của (H) tại điểm M ∈ (H) bất kì. Chứng minh rằng nếu ∆ cắt tiệm cận đứng và tiệm cận xiên của (H) tại A và B thì M luôn là trung điểm của đoạn AB.

Lời giải:

a) Tập xác định: D = ℝ\{−2}.

Ta có: $y^{'} = \frac{{mx}^{2} + 4 mx + 4 m - 1}{{(x + 2)}^{2}}$

y' = 0 ⇔ mx² + 4mx + 4m – 1 = 0

Xét ∆' = 4m² – m(4m – 1) = 4m² – 4m² + m = m.

Với m > 0 thì ta được y' = 0 là phương trình bâc hai có hai nghiệm phân biệt x₁, x₂.

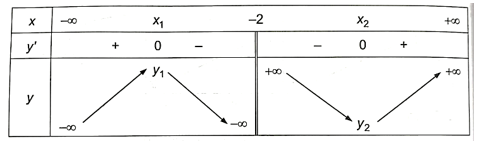
Bảng biến thiên của hàm số như sau:

Cho hàm số y trang 36 SBT Toán 12 Tập 1

Vậy hàm số luôn có cực đại, cực tiểu với mọi m > 0.

b) Với m = 1, ta có: y = $\frac{x^{2} + x - 1}{x + 2}$

Tập xác định: D = ℝ\{−2}.

Ta có: $y^{'} = \frac{x^{2} + 4 x + 3}{{(x + 2)}^{2}}$

y' = 0 ⇔ x² + 4x + 3 = 0 ⇔ x = −3 hoặc x = −1.

Ta có: $\lim_{x \to + \infty} y = + \infty; \lim_{x \to - \infty} y = - \infty$ .

$\lim_{x \to - 2^{+}} y = + \infty; \lim_{x \to - 2^{-}} y = - \infty$ .

Do đó, đồ thị hàm số nhận đường thẳng x = −2 làm tiệm cận đứng.

Ta có: y = $\frac{x^{2} + x - 1}{x + 2}$ = x – 1 + $\frac{1}{x + 2}$ .

Suy ra $\lim_{x \to + \infty} [y - (x - 1)] = \lim_{x \to + \infty} \frac{1}{x + 2} = 0$

Do đó, đường thẳng y = x – 1 là tiệm cận xiên của đồ thị hàm số.

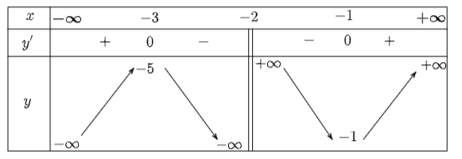
Ta có bảng biến thiên như sau:

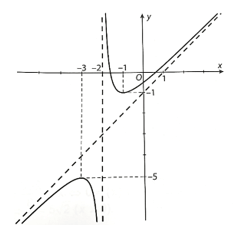
Cho hàm số y Chứng minh rằng hàm số đã cho luôn có cực đại, cực tiểu với mọi m lớn hơn 0

Đồ thị của hàm số như sau:

Cho hàm số y Chứng minh rằng hàm số đã cho luôn có cực đại, cực tiểu với mọi m lớn hơn 0

c) Lấy M $(t; \frac{t^{2} + t - 1}{t + 2})$ ∈ (H) bất kì.

Phương trình tiếp tuyến của đồ thị (H) tại M là:

d: y = y'(t)(x – t) + y(t)

y = $\frac{t^{2} + 4 t + 3}{{(t + 2)}^{2}} (x - t) + \frac{t^{2} + t - 1}{t + 2}$ .

Tiếp tuyến d cắt tiệm cận đứng tại điểm A $(- 2; - \frac{3 t + 4}{t + 2})$ .

Tiếp tuyến d cắt tiệm cận xiên tại điểm B(2t + 2; 2t + 1).

Ta có: $\{\begin{cases} x_{A} + x_{B} = 2 t = 2 x_{M} \\ y_{A} + y_{B} = (2 t + 1) - \frac{3 t + 4}{t + 2} = \frac{2 t^{2} + 2 t - 2}{t + 2} = 2 y_{M} \end{cases}$ .

Vậy M là trung điểm của đoạn AB.

Lời giải Sách bài tập Toán lớp 12 Bài tập cuối chương 1 hay khác:

SBT Toán 12 Kết nối

Cho hàm số y Chứng minh rằng hàm số đã cho luôn có cực đại, cực tiểu với mọi m lớn hơn 0

Giải sách bài tập Toán 12 Bài tập cuối chương 1 - Kết nối tri thức

Xem thêm các bài giải sách bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác: