Cho hàm số y = x^3 – 3x^2 + 2 có đồ thị (C) trang 36 SBT Toán 12 Tập 1

---

Giải sách bài tập Toán 12 Bài tập cuối chương 1 - Kết nối tri thức

Bài 1.64 trang 36 SBT Toán 12 Tập 1: Cho hàm số y = x³ – 3x² + 2 có đồ thị (C).

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.

b) Viết phương trình tiếp tuyến ∆ của đồ thị (C) tại tâm đối xứng của nó. Chứng minh rằng ∆ là tiếp tuyến có hệ số góc nhỏ nhất của (C).

c) Tìm các giá trị của tham số m để phương trình x³ – 3x² – m = 0 có ba nghiệm phân biệt.

Lời giải:

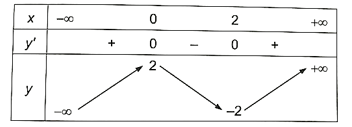
a) Tập xác định: D = ℝ.

Ta có: y' = 3x² – 6x²

           y' = 0 ⇔ 3x² – 6x² = 0 ⇔ x = 0 hoặc x = 2.

Hàm số đồng biến trên khoảng (−∞; 0) và (2; +∞).

Hàm số nghịch biến trên khoảng (0; 2).

Hàm số đạt cực đại tại điểm x = 0 và y_CĐ = y(0) = 2.

Hàm số đạt cực tiểu tại điểm x = 2 và y_CT = y(2) = −2.

Ta có: $\underset{x\to +\infty }{\lim }y=+\infty ;\underset{x\to -\infty }{\lim }y=-\infty$

Ta có bảng biến thiên như sau:

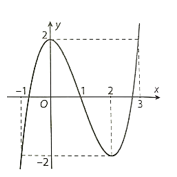
Đồ thị hàm số đi qua các điểm: (3; 2); (2; −2); (−1; −2); (0; 2).

Đồ thị hàm số có tâm đối xứng là điểm (1; 0).

Đồ thị hàm số như sau:

b) Tâm đối xứng của đồ thị hàm số là điểm I(1; 0).

Ta có: y'(1) = −3.

Vậy phương trình tiếp tuyến của đồ thị hàm số tại tâm đối xứng của nó là:

y = y'(1)(x – 1) + y(1)

   = −3(x – 1) + 0

   = −3x + 3 (∆).

Ta có: y' = 3x² – 6x = 3(x² – 2x + 1) – 3 = 3(x – 1)² – 3 ≥ −3 với mọi x.

Vậy ∆ là tiếp tuyến có hệ số góc nhỏ nhất của (C).

c) Ta có: x³ – 3x² – m = 0 ⇔ x³ – 3x² + 2 = m + 2.

Vậy phương trình x³ – 3x² – m = 0 là phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng y = m + 2. Suy ra, phương trình đã cho có ba nghiệm phân biệt khi và chỉ khi đường thẳng y = m + 2 cắt đồ thị (C) tại 3 điểm phân biệt, điều này tương đương với −2 < m + 2 < 2 ⇔ −4 < m < 0.  

Lời giải Sách bài tập Toán lớp 12 Bài tập cuối chương 1 hay khác:

• Bài 1.51 trang 33 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có đạo hàm trên (a;b). Xét các mệnh đề sau: ....

• Bài 1.52 trang 33 SBT Toán 12 Tập 1: Hàm số nào dưới đây nghịch biến trên tập xác định của nó? ....

• Bài 1.53 trang 33 SBT Toán 12 Tập 1: Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số ....

• Bài 1.54 trang 34 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có đạo hàm f'(x) = x(x – 1)²(x + 2)⁴ với mọi x ∈ ℝ. Số điểm cực trị của hàm số đã cho là: ....

• Bài 1.55 trang 34 SBT Toán 12 Tập 1: Cho hàm số $y=\frac{x^2+mx+1}{x+m}$ . Hàm số đạt cực đại tại x = 2 khi ....

• Bài 1.56 trang 34 SBT Toán 12 Tập 1: Cho hàm số $y=e^{-\frac{x^2}{2}}$  có đồ thị (C). Xét các mệnh đề sau: ....

• Bài 1.57 trang 34 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{1}{\sqrt{x}}$. Xét các mệnh đề sau: (I) Hàm số nghịch biến trên tập xác định của nó ....

• Bài 1.58 trang 34 SBT Toán 12 Tập 1: Cho hàm số $y=\frac{2x^2-4x+2}{x^2-6x+5}$. Mệnh đề nào sau đây là đúng? ....

• Bài 1.59 trang 34 SBT Toán 12 Tập 1: Giá trị lớn nhất của hàm số y = x² – 8lnx trên đoạn [1; e] là: ....

• Bài 1.60 trang 35 SBT Toán 12 Tập 1: Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như dưới đây: ....

• Bài 1.61 trang 35 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{ax+b}{cx+d}$  có đồ thị như hình vẽ sau: ....

• Bài 1.62 trang 35 SBT Toán 12 Tập 1: Biết đường thẳng y = 2x – 3 cắt đồ thị hàm số y = $\frac{2x+3}{x+3}$  tại hai điểm A và B ....

• Bài 1.63 trang 36 SBT Toán 12 Tập 1: Cho hàm số y = $\frac{1}{3}$ x³ + (m – 1)x² + (2m – 3)x + $\frac{2}{3}$ .a) Khảo sát sự biến thiên ....

• Bài 1.65 trang 36 SBT Toán 12 Tập 1: Cho hàm số $y=\frac{\left(m+1\right)x-2m+1}{x-1}$. a) Tìm m để tiệm cận ngang của ....

• Bài 1.66 trang 36 SBT Toán 12 Tập 1: Cho hàm số $y=\frac{m{x}^2+\left(2m-1\right)x-1}{x+2}$ với m là tham số ....

• Bài 1.67 trang 36 SBT Toán 12 Tập 1: Cắt bỏ hình quạt AOB (hình phẳng có nét gạch trong hình dưới đây) từ một mảnh ....

• Bài 1.68 trang 37 SBT Toán 12 Tập 1: Một hành lang giữa hai nhà có hình dạng một lăng trụ đứng (xem hình bên) ....