Hoạt động 10 trang 69 Toán 10 Tập 1 Cánh diều
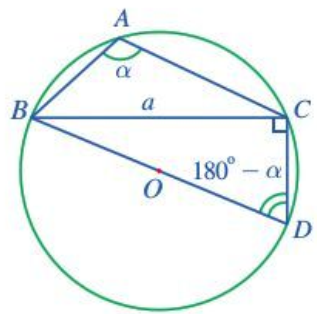
Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R và có BC = a, . Kẻ đường kính BD của đường tròn (O).
Giải Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180. Định lý côsin và định lý sin trong tam giác
Hoạt động 10 trang 69 Toán lớp 10 Tập 1: Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R và có BC = a, ^BAC=α . Kẻ đường kính BD của đường tròn (O).
Cho α là tù. Chứng minh:
a) ^BDC=180°−α;
b) asinα=2R.
Lời giải:
Do α là góc tù ta vẽ được hình như sau:
a) Tứ giác ABDC là tứ giác nội tiếp đường tròn (O) nên ^BAC+^BDC=180°(hai góc đối)
Suy ra ^BDC=180°−^BAC=180°−α.
Vậy ^BDC=180°−α.
b) Xét tam giác BCD, ta có ^BDC=180°−α và BD là đường kính của đường tròn (O) nên ^BCD=90°.
Do đó: sin^BDC=BCBD, tức là sin(180°−α)=a2R.
Mà sin(180° – α) = sin α nên sinα=a2R hay asinα=2R.
Lời giải bài tập Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°. Định lý côsin và định lý sin trong tam giác hay, chi tiết khác:
Luyện tập 2 trang 68 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 5, AC = 6, BC = 7. Tính cos A. ....
