Bài 7.22 trang 59 Toán 11 Tập 2 - Kết nối tri thức

Cho hình chóp .

Giải Toán 11 Bài 26: Khoảng cách - Kết nối tri thức

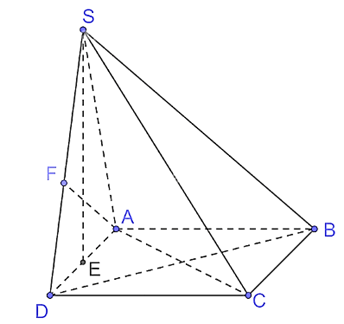
Bài 7.22 trang 59 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) $⊥$ (ABCD).

a) Tính chiều cao của hình chóp.

b) Tính khoảng cách giữa BC và (SAD).

c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD.

Lời giải:

Bài 7.22 trang 59 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Kẻ SE $⊥$ AD tại E.

Vì (SAD) $⊥$ (ABCD), (SAD) $\cap$ (ABCD) = AD mà SE $⊥$ AD nên SE $⊥$ (ABCD).

Vì tam giác SAD là tam giác đều cạnh a nên SE = $\frac{a \sqrt{3}}{2}$ .

Vậy chiều cao của hình chóp bằng $\frac{a \sqrt{3}}{2}$ .

b) Vì ABCD là hình vuông nên BC // AD, suy ra BC // (SAD).

Khi đó d(BC, (SAD)) = d(B, (SAD)).

Vì ABCD là hình vuông nên AB $⊥$ AD mà SE $⊥$ (ABCD) nên SE $⊥$ AB.

Vì AB $⊥$ AD và SE $⊥$ AB nên AB $⊥$ (SAD).

Do đó d(BC, (SAD)) = d(B, (SAD)) = AB = a.

c) Kẻ AF $⊥$ SD tại F, mà AB $⊥$ (SAD) nên AB $⊥$ AF.

Vì AF $⊥$ SD và AB $⊥$ AF nên AF là đường vuông góc chung của AB và SD.

Vì tam giác SAD đều có AF là đường cao nên AF = $\frac{a \sqrt{3}}{2}$ .

Vậy d(AB, SD) = AF = $\frac{a \sqrt{3}}{2}$ .

Lời giải bài tập Toán 11 Bài 26: Khoảng cách hay, chi tiết khác: