HĐ4 trang 57 Toán 11 Tập 2 - Kết nối tri thức

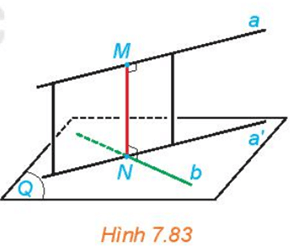
Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a' của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83).

Giải Toán 11 Bài 26: Khoảng cách - Kết nối tri thức

HĐ4 trang 57 Toán 11 Tập 2: Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a' của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83).

a) Mặt phẳng chứa a và a' có vuông góc với (Q) hay không?

b) Đường thẳng MN có vuông góc với cả hai đường thẳng a và b hay không?

c) Nêu mối quan hệ của khoảng cách giữa a, (Q) và độ dài đoạn thẳng MN.

Lời giải:

a) Vì a' là hình chiếu của a trên (Q) nên a và a' thuộc cùng một mặt phẳng. Hơn nữa, mặt phẳng đó chứa phương chiếu là đường thẳng vuông góc với (Q) nên mặt phẳng chứa a và a' vuông góc với (Q).

b) Gọi mặt phẳng chứa a và a' là mặt phẳng (P).

Vì a // (Q) và (P) $\cap$ (Q) = a' nên a // a'.

Vì MN $\perp$ a nên MN $\perp$ a'.

Trong mặt phẳng (P) có MN và phương chiếu vuông góc lên (Q) cùng vuông góc với a nên chúng song song với nhau. Do đó MN $\perp$ (Q) nên MN $\perp$ b.

c) Vì a // (Q) nên d(a, (Q)) = d(M, (Q)) = MN (vì MN $\perp$ (Q)).

Lời giải bài tập Toán 11 Bài 26: Khoảng cách hay, chi tiết khác:

• HĐ1 trang 54 Toán 11 Tập 2: a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a ....

• Luyện tập 1 trang 55 Toán 11 Tập 2: Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a ....

• HĐ2 trang 55 Toán 11 Tập 2: Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M; N bất kỳ thuộc a ....

• HĐ3 trang 56 Toán 11 Tập 2: a) Cho hai đường thẳng m và n song song với nhau. Khi một điểm M thay đổi trên m thì khoảng cách ....

• Câu hỏi trang 56 Toán 11 Tập 2: Nếu đường thẳng a thuộc mặt phẳng (P) và mặt phẳng (Q) song song với (P) ....

• Luyện tập 2 trang 56 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng ....

• Vận dụng 1 trang 57 Toán 11 Tập 2: Ở một con dốc lên cầu, người ta đặt một khung khống chế chiều cao ....

• Khám phá trang 58 Toán 11 Tập 2: Cho đường thẳng a vuông góc với mặt phẳng (P) và cắt (P) tại O ....

• Luyện tập 3 trang 58 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD) ....

• Thảo luận trang 58 Toán 11 Tập 2: Khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) ....

• Bài 7.22 trang 59 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD ....

• Bài 7.23 trang 59 Toán 11 Tập 2: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a ....

• Bài 7.24 trang 59 Toán 11 Tập 2: Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB ....

• Bài 7.25 trang 59 Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' có cạnh a. ....

• Bài 7.26 trang 59 Toán 11 Tập 2: Giá đỡ ba chân ở Hình 7.90 đang được mở sao cho ba gốc chân cách đều nhau ....

• Bài 7.27 trang 59 Toán 11 Tập 2: Một bể nước có đáy thuộc mặt phẳng nằm ngang. Trong trường hợp này ....