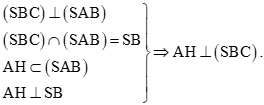Luyện tập 2 trang 56 Toán 11 Tập 2 - Kết nối tri thức
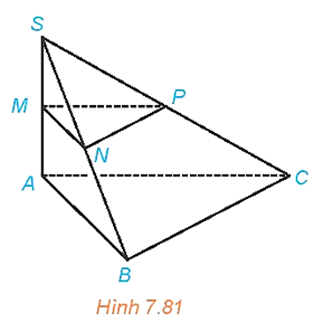
Cho hình chóp S.ABC có SA (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
Giải Toán 11 Bài 26: Khoảng cách - Kết nối tri thức
Luyện tập 2 trang 56 Toán 11 Tập 2: Cho hình chóp S.ABC có SA (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) Tính d((MNP), (ABC)) và d(NP, (ABC)).
b) Giả sử tam giác ABC vuông tại B và AB = a. Tính d(A, (SBC)).
Lời giải:
a) Xét tam giác SAB có M là trung điểm của SA, N là trung điểm của SB nên MN là đường trung bình của tam giác SAB suy ra MN // AB, do đó MN // (ABC).
Xét tam giác SBC có N là trung điểm của SB, P là trung điểm của SC nên PN là đường trung bình của tam giác SBC suy ra PN // BC, do đó PN // (ABC).
Vì MN // (ABC) và PN // (ABC) mà MN PN = N nên (MNP) // (ABC).
Khi đó d((MNP), (ABC)) = d(M, (ABC)).
Vì SA (ABC) nên MA (ABC). Do đó d(M, (ABC)) = MA.
Vì M là trung điểm SA nên AM = .
Do đó d((MNP), (ABC)) = .
Vì PN // (ABC) nên d(NP, (ABC)) = d(N, (ABC)).
Vì MN // (ABC) nên d(N, (ABC)) = d(M, (ABC)) = MA = .
Vậy d(NP, (ABC)) = .
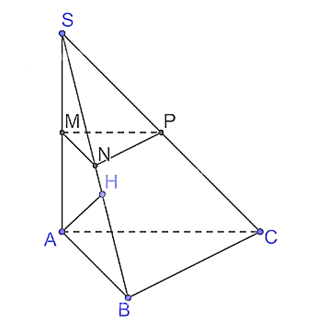
b) Vì ABC là tam giác vuông tại B nên BC AB.
Vì SA (ABC) nên SA BC mà BC AB nên BC (SAB), suy ra (SBC) (SAB).
Kẻ AH SB tại H.
Vì
Khi đó d(A, (SBC)) = AH.
Vì SA (ABC) nên SA AB.
Xét tam giác SAB vuông tại A, AH là đường cao, có
.
Vậy d(A, (SBC)) = .
Lời giải bài tập Toán 11 Bài 26: Khoảng cách hay, chi tiết khác:
Khám phá trang 58 Toán 11 Tập 2: Cho đường thẳng a vuông góc với mặt phẳng (P) và cắt (P) tại O ....