Bài 4.8 trang 78 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

❮ Bài trước Bài sau ❯

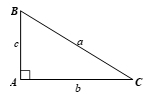
Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp:

Giải Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng - Kết nối tri thức

Bài 4.8 trang 78 Toán 9 Tập 1: Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp:

a) a = 21, b = 18;

b) b = 10, $\hat{C} = 30 °;$

c) c = 5, b = 3.

Lời giải:

Bài 4.8 trang 78 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

a) Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có: a² = b² + c²

Suy ra $c = \sqrt{a^{2} - b^{2}} = \sqrt{21^{2} - 18^{2}} = \sqrt{117} = \sqrt{3^{2} \cdot 13} = 3 \sqrt{13}$ (do c > 0).

Theo định nghĩa tỉ số lượng giác sin, ta có $\sin B = \frac{b}{a} = \frac{18}{21} = \frac{6}{7} .$ Từ đó tìm được $\hat{B} \approx 59 ° .$

Theo định lí tổng ba góc của một tam giác, ta có $\hat{A} + \hat{B} + \hat{C} = 180 ° .$

Suy ra $\hat{C} = 90 ° - \hat{B} \approx 90 ° - 59 ° = 31 ° .$

Vậy ∆ABC có $\hat{A} = 90 °, \hat{B} \approx 59 °, \hat{C} \approx 31 °, a = 21, b = 18, c = 3 \sqrt{13} .$

b) Xét ∆ABC vuông tại A, theo định lí tổng ba góc của một tam giác, ta có: $\hat{A} + \hat{B} + \hat{C} = 180 ° .$

Suy ra $\hat{B} = 90 ° - \hat{C} = 90 ° - 30 ° = 60 ° .$

Theo định lí 2, ta có: $A B = c = b \cdot t a n C = 10 \cdot t a n 30 ° = \frac{10 \sqrt{3}}{3} .$

Theo định lí 1, ta có AC = b = a.cosC, suy ra $a = \frac{b}{\cos C} = \frac{10}{\cos 30 °} = \frac{10}{\frac{\sqrt{3}}{2}} = \frac{20}{\sqrt{3}} = \frac{20 \sqrt{3}}{3} .$

Vậy ∆ABC có $\hat{A} = 90 °, \hat{B} = 60 °, \hat{C} = 30 °, a = \frac{20 \sqrt{3}}{3}, b = 10, c = \frac{10 \sqrt{3}}{3} .$

c) Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có: a² = b² + c²

Suy ra $a = \sqrt{b^{2} + c^{2}} = \sqrt{3^{2} + 5^{2}} = \sqrt{34}$ (vì a > 0).

Theo định nghĩa tỉ số lượng giác tan, ta có $\tan B = \frac{b}{c} = \frac{3}{5},$ suy ra $\hat{B} \approx 31 ° .$

Theo định lí tổng ba góc của một tam giác, ta có $\hat{A} + \hat{B} + \hat{C} = 180 ° .$

Suy ra $\hat{C} = 90 ° - \hat{B} \approx 90 ° - 31 ° = 59 ° .$

Vậy ∆ABC có $\hat{A} = 90 °, \hat{B} \approx 31 °, \hat{C} \approx 59 °, a = \sqrt{34}, b = 3, c = 5.$

Lời giải bài tập Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Toán 9 Kết nối tri thức

Bài 4.8 trang 78 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng - Kết nối tri thức

Xem thêm lời giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác: