Mở đầu trang 74 Toán 9 Tập 2 | Kết nối tri thức Giải Toán 9

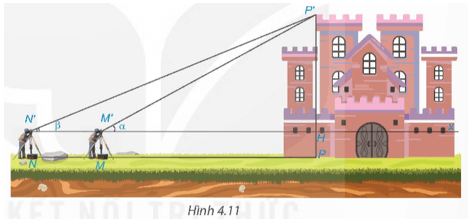
Để đo chiều cao của một toà lâu đài (H.4.11), người ta đặt giác kế thẳng đứng tại điểm M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P’ của toà lâu đài dưới góc nhọn α. Sau đó, đặt giác kế thẳng đứng tại điểm N, NM = 20 m, thì nhìn thấy đỉnh P’ dưới góc nhọn β (β < α). Biết chiều cao giác kế là 1,6 m, hãy tính chiều cao của toà lâu đài.

Giải Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng - Kết nối tri thức

Mở đầu trang 74 Toán 9 Tập 2: Để đo chiều cao của một toà lâu đài (H.4.11), người ta đặt giác kế thẳng đứng tại điểm M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P’ của toà lâu đài dưới góc nhọn α. Sau đó, đặt giác kế thẳng đứng tại điểm N, NM = 20 m, thì nhìn thấy đỉnh P’ dưới góc nhọn β (β < α). Biết chiều cao giác kế là 1,6 m, hãy tính chiều cao của toà lâu đài.

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Xét ∆M’P’H vuông tại H, theo định lí 2, ta có: M’H = P’H.cotα.

Xét ∆N’P’H vuông tại H, theo định lí 2, ta có: N’H = P’H.cotβ.

Mà N’H = N’M’ + M’H = MN + M’H

Do đó P’H.cotβ = MN + P’H.cotα.

Suy ra P’H.(cotβ – cotα) = MN nên $P^{\text{'}}H=\frac{MN}{cot\beta –cot\alpha }=\frac{20}{cot\beta –cot\alpha }.$

Vì vậy, $P^{\text{'}}P=P^{\text{'}}H+HP=\frac{20}{cot\beta –cot\alpha }+\mathrm{1,6}\text{ (m).}$

Vậy chiều cao của tòa nhà là $P^{\text{'}}P=\frac{20}{cot\beta –cot\alpha }+\mathrm{1,6}\text{ (m).}$

Lời giải bài tập Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng hay, chi tiết khác:

• HĐ1 trang 74 Toán 9 Tập 1: Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c (H.4.12) ....

• Luyện tập 1 trang 75 Toán 9 Tập 1: Một chiếc thang dài 3 m. Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu mét ....

• HĐ2 trang 75 Toán 9 Tập 1: Xét tam giác ABC trong Hình 4.16 ....

• Luyện tập 2 trang 76 Toán 9 Tập 1: Bóng trên mặt đất của một cây dài 25 m. Tính chiều cao của cây (làm tròn đến dm) ....

• Luyện tập 3 trang 77 Toán 9 Tập 1: Cho tam giác vuông ABC có cạnh góc vuông AB = 4, cạnh huyền BC = 8 ....

• Câu hỏi trang 77 Toán 9 Tập 1: Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh AB = c, AC = b ....

• Luyện tập 4 trang 77 Toán 9 Tập 1: Giải tam giác ABC vuông tại A, biết BC = 9, $\widehat{C}=53°.$ ....

• Vận dụng trang 77 Toán 9 Tập 1: Giải bài toán ở tình huống mở đầu với α = 27° và β = 19° ....

• Bài 4.8 trang 78 Toán 9 Tập 1: Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp ....

• Bài 4.9 trang 78 Toán 9 Tập 1: Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22 ....

• Bài 4.10 trang 78 Toán 9 Tập 1: Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23 ....

• Bài 4.11 trang 78 Toán 9 Tập 1: Tính các góc của hình thoi có hai đường chéo dài $2\sqrt{3}$ và 2 ....

• Bài 4.12 trang 78 Toán 9 Tập 1: Cho hình thang ABCD (AD // BC) có AD = 16 cm, BC = 4 cm và $\widehat{A}=\widehat{B}=\widehat{ACD}=90°.$ ....

• Bài 4.13 trang 78 Toán 9 Tập 1: Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m ....