Đề thi Toán lớp 9 Học kì 1 năm 2023 có đáp án (4 đề)

---

Haylamdo biên soạn và sưu tầm Đề thi Toán lớp 9 Học kì 1 năm 2023 có đáp án (4 đề - Sách Mới) được tổng hợp chọn lọc từ đề thi môn Toán 9 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 9.

Đề thi Toán lớp 9 Học kì 1 năm 2023 có đáp án (4 đề - Sách Mới)

Xem thử

Chỉ 100k mua trọn bộ Đề thi Toán 9 Học kì 1 bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

Ma trận đề thi HK1 Toán 9

Mức độ Chủ đề	Nhận biết	Thông hiểu	Vận dụng		Cộng
			Cấp độ thấp	Cấp độ cao
	Tự luận	Tự luận	Tự luận	Tự luận
1. Căn thức bậc hai	Hiểu được khái niệm căn bậc 2 để giải toán tìm x	Hiểu được hằng đẳng thức để thực hiện phép tính	Vận dụng các phép biến đổi đơn giản để rút gọn biểu thức, tính giá trị biểu thức	Vận dụng các phép biến đổi để rút gọn biểu thức phức tạp, giải phương trình vô tỷ
	Số câu: 2 Số điểm:1	Số câu: 2 Số điểm:1	Số câu: 2 Số điểm: 1,5.	Số câu: 1 Số điểm:0,5	Số câu: 7 Số điểm: 4
2. Hàm số bậc nhất	Nắm được các khái niệm cơ bản về hàm số như tính đồng biến nghịch biến, điểm thuộc hay không thuộc hàm số…	Hiểu được hai đường thẳng song song, cắt nhau, giao điểm của hai đường thẳng. Vẽ được đồ thị hàm số.	Tìm được điềm m thảo mãn điều kiện cho trước.
	Số câu:1 Số điểm: 0,5	Số câu: 2 Số điểm:1	Số câu:1 Số điểm:1		Số câu: 4 Số điểm: 2,5
3. Hệ thức lượng trong tam giác vuông.			Vận dụng các hệ thức lượng trong tam giác vuông để giải toán
			Số câu:1 Số điểm: 0,5		Số câu: 1 Số điểm:0,5
4. Đường tròn	Nhận biết được đường tròn	Hiểu được tính chất đường tròn, hai tiếp tuyến cắt nhau để chứng minh	Vận dụng khái niệm đường tròn và các tính chất đường tròn, hai tiếp tuyến cắt nhau của đường tròn để chứng minh
	Số câu: 1 Số điểm: 1	Số câu:1 Số điểm:1	Số câu:1 Số điểm 1		Số câu: 3 Số điểm: 3
Tổng	Số câu: 4 Số điểm: 2,5	Số câu: 5 Số điểm: 3	Số câu: 5 Số điểm: 4,0	Số câu: 1 Số điểm: 0,5	Số câu: 15 Số điểm: 10

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1 theo Thông tư 22

Năm học 2023

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 1)

Xem miễn phí

Câu 1 (1 điểm): Thực hiện phép tính

a)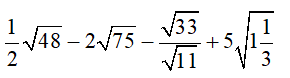

b)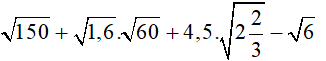

Câu 2 (1 điểm): Tìm x

a)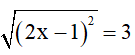

b)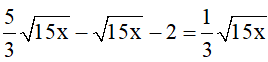

Câu 3 (1,5 điểm): Cho biểu thức

B =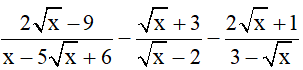

a) Tìm điều kiện xác định và rút gọn B.

b) Tìm x nguyên để P nguyên.

Câu 4 (2,5 điểm): Cho đường thẳng d: y = mx + 1 (m ≠ 0).

a) Tìm m để hàm số đã cho đồng biến.

b) Tìm m để (d) song song với đường thẳng y = 2x + 5.

c) Biết d cắt hai trục Ox và Oy tại hai điểm A và B. Tìm m để diện tích tam giác OAB bằng 1.

Câu 5 (3,5 điểm):

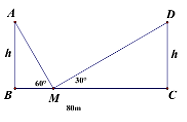
1. Hai trụ điện có cùng chiều cao h được dựng thẳng đứng bên lề đối diện một đại lộ rộng 80 m. Từ một điểm M trên mặt đường nằm giữa hai trụ điện người ta nhìn thấy đỉnh hai trụ điện với góc nâng lần lượt 60' và 30'. Tính chiều cao trụ điện? (làm tròn đến chữ số thập phân thứ hai).

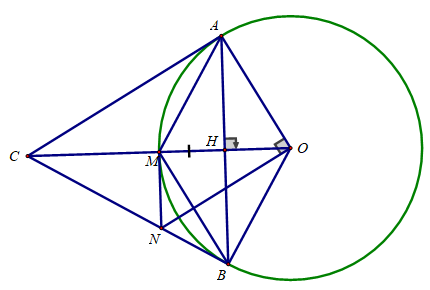
2. Cho đừng tròn (O; R) và đường thẳng d cố định không cắt đường tròn. Từ một điểm A bất kỳ trên đường thẳng d kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Từ B kẻ đường thẳng vuông góc với AO tại H, trên tia đối của tia HB lấy điểm C sao cho HC = HB.

a) Chứng minh C thuộc đường tròn (O; R) và AC là tiếp tuyến của đường tròn (O; R).

b) Từ điểm O kẻ đường thẳng vuông góc với đường thẳng d tại I, OI cắt BC tại K. Chứng minh: OH.OA = OI.OK = R².

c) Chứng minh khi A thay đổi trên đường thẳng d thì đường thẳng BC luôn đi qua một điểm cố định.

Câu 6 (0,5 điểm): Giải phương trình: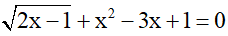

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1 theo Thông tư 22

Năm học 2023

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 2)

Bài 1 (1 điểm): Thực hiện phép tính

a)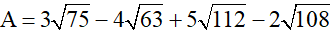

b)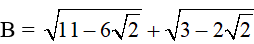

Bài 2 (1 điểm): Tìm x

a)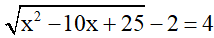

b)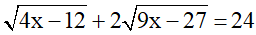

Bài 3 (1,5 điểm): Cho biểu thức: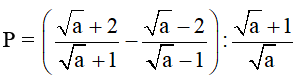(với a > 0; a ≠ 1)

a) Rút gọn P

b) Tính giá trị của P khi a = 3 + 2√2.

Bài 4 (2,5 điểm): Cho hai đường thẳng (d): y = 3x – 1 và (d1) : y = x + 2

a) Vẽ đồ thị (d) và (d1)trên cùng một mặt phẳng tọa độ Oxy.

b) Xác định tọa độ giao điểm của hai đường thẳng (d) và (d1) bằng phương pháp tọa độ.

c) Viết phương trình đường thẳng : y = ax + b , biết song song với (d) và (d1) cắt trục hoành tại điểm có hoành độ bằng 1.

Bài 5 (3,5 điểm):

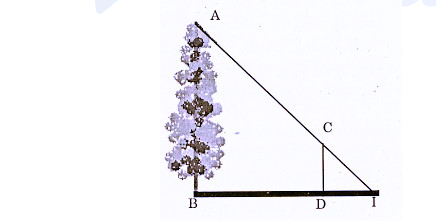
1. Để đo chiều cao của một cái cây bằng ánh nắng mặt trời, bạn An cắm một cọc CD thẳng đứng cách cây 24 mét khi bóng của cây trùng với bóng của cọc bạn An đánh dấu vị trí I. Đo khoảng cách ID được 1,6 mét. Hỏi chiều cao AB của cây? (Biết cọc có chiều cao 1,2 mét)

2. Cho đường tròn (O; 6cm), điểm A nằm bên ngoài đường tròn,

OA = 12cm. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm).

a) Chứng minh BC vuông góc với OA.

b) Kẻ đường kính BD, chứng minh OA // CD.

c) Gọi K là giao điểm của AO với BC. Tính tích: OK.OA và số đo góc .

Bài 6 (0,5 điểm): Giải phương trình sau:

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1 theo Thông tư 22

Năm học 2023

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 3)

Bài 1 (1 điểm): Tìm x

a)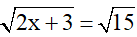

b)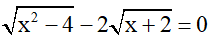

Bài 2 (1 điểm): Thực hiện phép tính

a)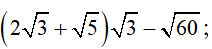

b)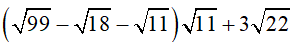

Bài 3 (1,5 điểm): Cho biểu thức: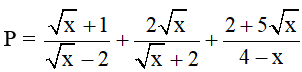

a) Rút gọn P biết x ≥ 0, x ≠ 4.

b) Tìm x để P = 2.

Bài 4 (2,5 điểm):

a) Cho đường thẳng d₁: y = (2m +1)x + 3m – 2. Tìm m để hàm số đã cho đi qua A(1; 2).

b) Vẽ đồ thị hàm số d: y = -4x + 3.

c) Cho đường thẳng d₃: y = 3x + m – 1. Tìm m để khoảng cách từ O đến d bằng 2

Bài 5 (3,5 điểm):

1. Một cái thang khi dựa vào tường thì góc a giữa thang và mặt đất trong khoảng từ 60^o đến 65^o thì an toàn. Hỏi một cái thang AB dài 3m dựng vào tường thì chân thang A cách chân tường C trong khoảng nào thì an toàn? (làm tròn 2 chữ số thập phân).

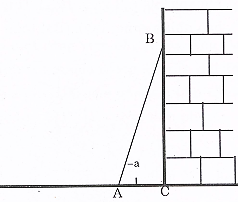
2. Từ điểm A nằm ngoài đường tròn (O; R), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B, C là hai tiếp điểm). Gọi H là giao điểm của OA và BC.

a) Chứng minh: OA là đường trung trực của BC và OH.OA = R².

b) Đoạn thẳng OA cắt đường tròn (O) tại M. Chứng minh: BM là tia phân giác của góc ABH.

c) Trên đoạn AH lấy điểm D sao cho HB = HD, qua D kẻ DE vuông góc với OA (E thuộc AB), gọi I là trung điểm OE. Tính số đo góc BHI và độ dài cạnh BE theo R.

Bài 6 (0,5 điểm): Giải phương trình:

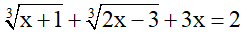
Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2023

Môn: Toán 9

Thời gian làm bài: 90 phút

(Đề thi số 4)

Câu 1: 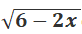có nghĩa khi:

A.x ≥ 3       B.x > 3       C.x < 3       D.x ≤ 3

Câu 2: Kết quả của phép tính 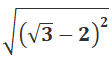là:

A.√3 - 2       B. 2 - √3       C. 1       D. Kết quả khác

Câu 3: 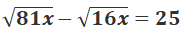khi đó x bằng:

A. 25       B. 9       C. – 25       D. – 9

Câu 4: Hai đường thẳng y = ax + 2 và y = 4x + 5 song song với nhau khi :

A. a = - 4       B. a ≠ 4       C. a = 4       D. a ≠ -4

Câu 5: Hàm số y = (m - 3)x + 3 nghịch biến khi m nhận giá trị:

A.m > 3       B.m < 3       C.m ≥ 3       D.m ≤ 3

Câu 6: Cho tam giác BDC vuông tại D, ∠B = 60^o , BD = 3 cm. Độ dài cạnh DC bằng:

A.3 cm       B.3√3 cm       C.√3 cm       D.12 cm

Câu 7: Đẳng thức nào sau đây là đúng:

A.sin 50^o = cos 30^o       B.tan 40^o = cotg 60^o

C.cotg 50^o = tan 45^o       D.sin 58^o = cos 32^o

Câu 8: Cho đoạn thẳng OI = 8 cm. Vẽ các đường tròn (O; 10cm); (I; 2cm). Hai đường tròn (O) và (I) có vị trí tương đối như thế nào với nhau?

A. (O) và (I) tiếp xúc trong với nhau

B. (O) và (I) tiếp xúc ngoài với nhau

C. (O) và (I) cắt nhau

D. (O) và (I) không cắt nhau

Phần tự luận (8 điểm)

Bài 1 (2,5 điểm) Cho biểu thức

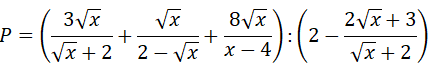
a) Rút gọn P

b) Tính giá trị của P biết

c) Tìm m để có một giá trị x thỏa mãn :

P(√x - 2) + √x (m - 2x) - √x = m - 1

Bài 2 (2 điểm) Cho hàm số y =(m – 3)x + 2 có đồ thị là (d)

a) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng – 3. Khi đó (d) tạo với trục Ox một góc nhọn hay góc tù. Vì sao?

b) Vẽ đồ thị với m tìm được ở câu a.

c) Tìm m để (d) cắt hai trục tọa độ tạo thành một tam giác có diện tích bằng 4.

Bài 3 (3,5 điểm) Cho nửa đường tròn (O; R) đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E.

a) Chứng minh rằng AD + BE = DE

b) AC cắt DO tại M, BC cắt OE tại N. Tứ giác CMON là hình gì? Vì sao?

c) Chứng minh rằng OM.OD + ON.OE không đổi

d) AN cắt CO tại điểm H. Điểm H di chuyển trên đường nào khi C di chuyển trên nửa đường tròn (O; R).

Hướng dẫn giải

Phần trắc nghiệm (2 điểm)

1.D	2.B	3.A	4.C
5.B	6.B	7.D	8.A

Phần tự luận (8 điểm)

Bài 1

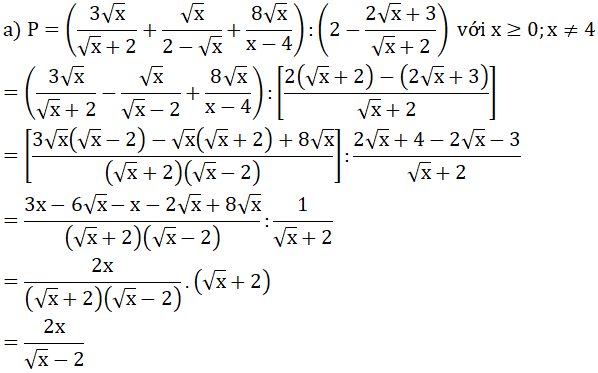
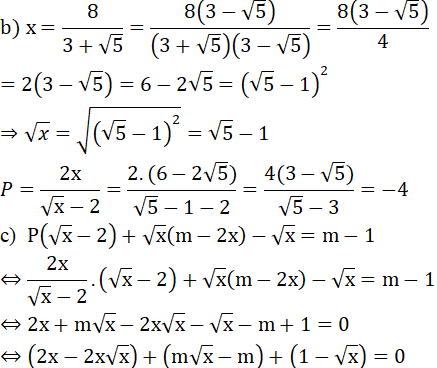
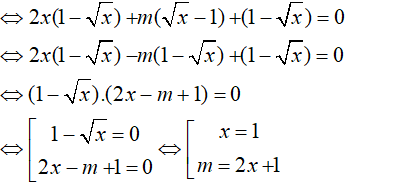
Để tồn tại 1 giá trị của x thỏa mãn đề bài thì: m = 2x + 1 phải thỏa mãn với x = 1

Thay x = 1 vào ta được: m = 2.1 + 1 = 3

Vậy m = 3 thỏa mãn đầu bài.

Bài 2 Cho hàm số y = (m – 3)x + 2 có đồ thị là (d)

a) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng – 3 khi:

0 = (m - 3).(-3) + 2 ⇔ 3m = 11 ⇔ m = 11/3

Khi đó (d) có phương trình là:

y = (11/3 - 3)x + 2 = 2/3 x + 2

Có hệ số a = 2/3 > 0

⇒ (d) tạo với trục Ox một góc nhọn

b) Tập xác định của hàm số R

Bảng giá trị

x	0	- 3
y = 2/3 x + 2	2	0

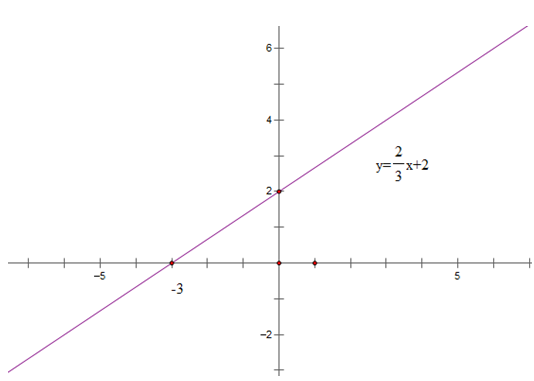
c) y = (m – 3)x + 2 (m ≠ 3)

Gọi A, B lần lượt là giao điểm của (d) và trục Ox, Oy và tam giác tạo thành là tam giác AOB vuông tại O

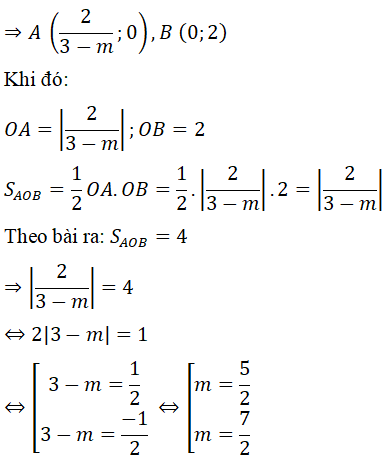
Bài 3

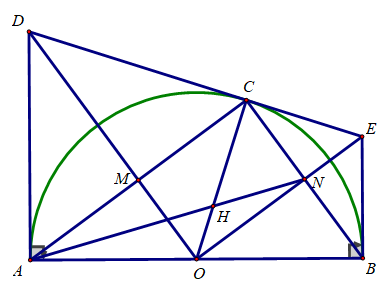
a) CE và EB là 2 tiếp tuyến cắt nhau tại E

⇒ EC = EB và CB ⊥ OE

Tương tự, DC và DA là 2 tiếp tuyến cắt nhau tại D

⇒ DC = DA và AC ⊥ OD

Khi đó: AD + BE = DC + EC = DE

b) Xét tứ giác OMCN có:

∠(OMC) = 90^o (AC ⊥ OD)

∠(ONC) = 90^o (CB ⊥ OE)

∠(NCM) = 90^o (AC ⊥ CB)

⇒ Tứ giác OMCN là hình chữ nhật

c) Xét tam giác DOC vuông tại C, CM là đường cao có:

OM.OD = OC² = R²

Xét tam giác EOC vuông tại C, CN là đường cao có:

ON.OE = OC² = R²

Khi đó: OM.OD + ON.OE = 2R²

Vậy OM.OD + ON.OE không đổi

d) Ta có: N là trung điểm của BC

⇒ AN là trung tuyến của ΔABC

CO cũng là trung tuyến của ΔABC

AN ∩ CO = H

⇒ H là trọng tâm ΔABC

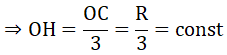
Vậy khi C di chuyển trên nửa đường tròn (O) thì H di chuyển trên nửa đường tròn

(O; R/3)

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2023

Môn: Toán 9

Thời gian làm bài: 90 phút

(Đề thi số 5)

Bài 1: (1.5 điểm) Thực hiện các phép tính:

a) (√75 - 3√2 - √12)(√3 + √2)

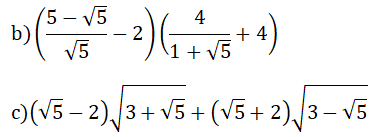
Bài 2: (1.5 điểm) Giải phương trình

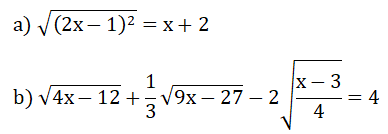
Bài 3: (1.5 điểm) Cho hàm số y = –2x + 3 có đồ thị (d₁) và hàm số y = x – 1 có đồ thị (d₂)

a) Vẽ (d₁) và (d₂) trên cùng một mặt phẳng tọa độ.

b) Xác định hệ số a và b biết đường thẳng (d₃): y = ax + b song song với (d₂) và cắt (d₁) tại điểm nằm trên trục tung.

Bài 4: (2 điểm) Cho biểu thức :

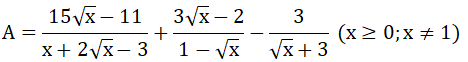
a) Thu gọn biểu thức A.

b) Tìm x nguyên để A nguyên.

Bài 5: (3.5 điểm) Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.

a) Chứng minh MD là tiếp tuyến của đường tròn (O).

b) Kẻ đường kính CE của đường tròn (O). Tính MC, DE theo R.

c) Chứng minh HA² + HB² + CD²/2 = 4R²

d) ME cắt đường tròn (O) tại F (khác E). Chứng minh: ∠(MOF) = ∠(MEH )

Đáp án và Hướng dẫn giải

Bài 1: (1.5 điểm)

a) (√75 - 3√2 - √12)(√3 + √2)

=(5√3 - 3√2 - 2√3)(√3 + √2)

=3(√3 - √2)(√3 + √2) = 3

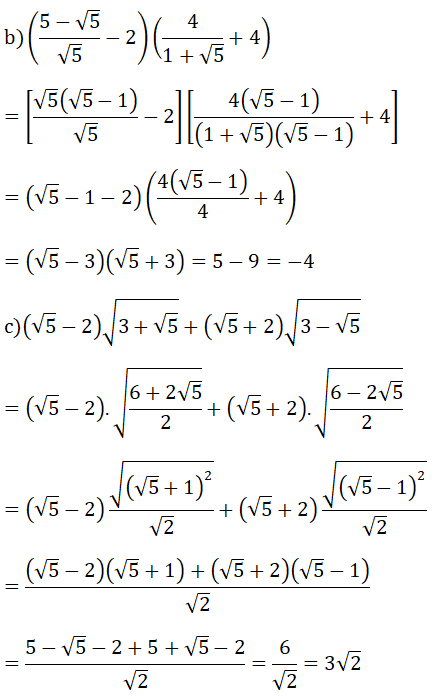
Bài 2: (1.5 điểm)

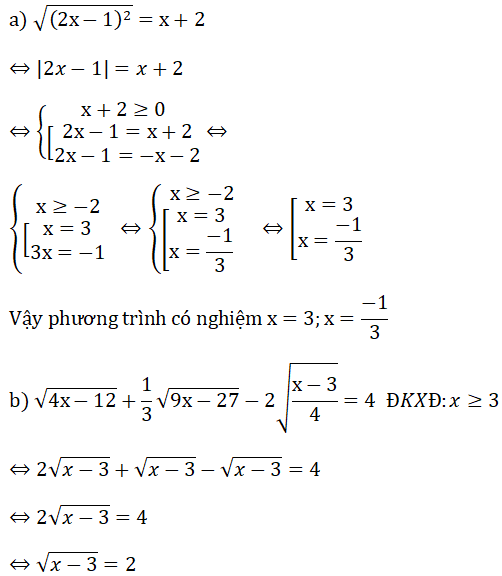
⇔ x - 3 = 4

⇔ x = 7 (TM ĐKXĐ)

Vậy phương trình có nghiệm x = 7

Bài 3: (1.5 điểm)

a) Tập xác định của hàm số R

Bảng giá trị

x	0	1
y = -2x + 3	3	1

x	0	1
y = x – 1	- 1	0

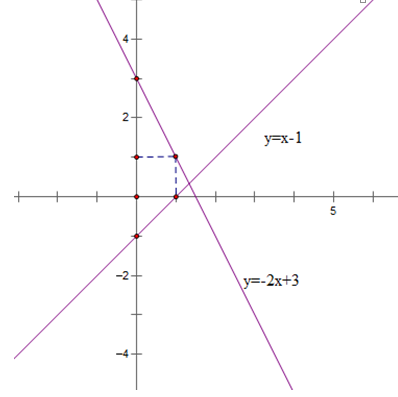
b) Do (d₃ ) song song với đường thẳng (d₂ ) nên (d₃ ) có dạng: y = x + b (b ≠ -1)

(d₁ ) cắt trục tung tại điểm (0; 3)

Do (d₃ ) cắt (d₁ ) tại điểm nằm trên trục tung nên ta có:

3 = 0 + b ⇔ b = 3

Vậy phương trình đường thẳng (d₃ ) là y = x + 3

Bài 4: (2 điểm)

x + 2√x - 3 = x - √x + 3√x - 3 = √x (√x - 1) + 3(√x - 1) = (√x - 1)(√x + 3)

a) Với điểu kiện x ≥ 0; x ≠ 1 ta có:

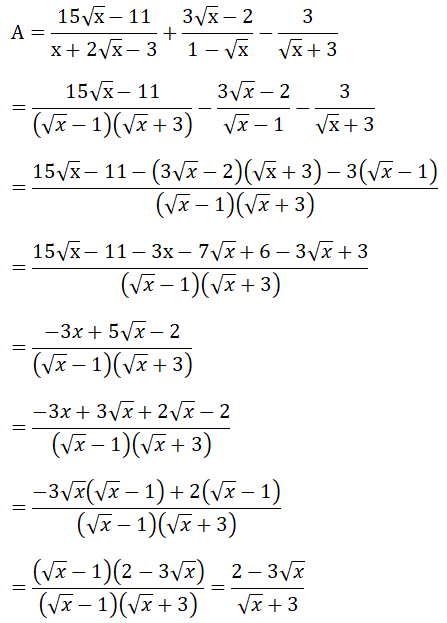
b) Tìm x nguyên để A nguyên

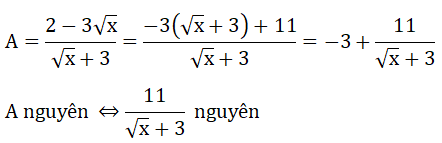
⇔ √x + 3 ∈ Ư(11) ⇔ √x + 3 ∈ {-11; -1; 1; 11}

Do √x + 3 ≥ 3 nên √x + 3 = 11 ⇔ √x = 8 ⇔ x = 64

Vậy với x = 64 thì A nguyên

Bài 5: (3.5 điểm)

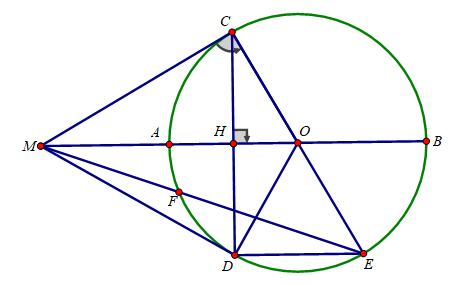
a) Xét tam giác COD cân tại O có OH là đường cao

⇒ OH cũng là tia phân giác ⇒ ∠(COM) = ∠(MOD)

Xét ΔMCO và ΔMOD có:

CO = OD

∠(COM) = ∠(MOD)

MO là cạnh chung

⇒ ΔMCO = ΔMOD (c.g.c)

⇒ ∠(MCO) = ∠(MDO)

∠(MCO) = 90^o nên ∠(MDO) = 90^o

⇒ MD là tiếp tuyến của (O)

b) Ta có: OM = OA + AM = R + R = 2R

Xét tam giác MCO vuông tại C, CH là đường cao có:

MO² = MC² + OC²

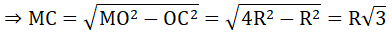
CH.OM = CM.CO

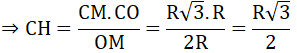
Lại có: CD = 2CH ⇒ CD = R√3

Tam giác CDE nội tiếp (O) có CE là đường kính nên ΔCDE vuông tại D

Theo định lí Py ta go ta có:

CE² = CD² + DE²

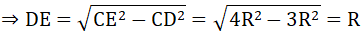
c) Ta có: ΔCOD cân tại O có OH là đường cao cũng là đường trung tuyến của tam giác

⇒ CH = HD = CD/2 ⇒ CH² = DH² = CD² /4

Tam giác ACH vuông tại H có:

AH² + CH² = CA² ⇒ AH² + CD²/4 = CA² (1)

Tam giác CHB vuông tại H có:

BH² + CH² = CB² ⇒ BH² + CD²/4 = CB² (2)

Từ (1) và (2) ta có:

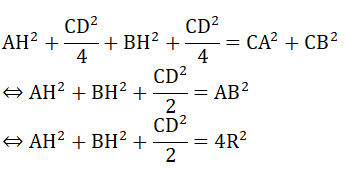
d) Ta có: ∠(CFE) = 90^o (F thuộc đường tròn đường kính CE)

Lại có CF là đường cao nên MC² = MF.ME

Tương tự, ta có: MC² = MH.MO

⇒ ME.MF = MH.MO

⇒

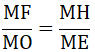
Xét ΔMOF và ΔMEN có:

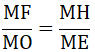
∠(FMO) chung

⇒ ΔMOF ∼ ΔMEN (c.g.c)

⇒ ∠(MOF) = ∠(MEH)

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2023

Môn: Toán 9

Thời gian làm bài: 90 phút

(Đề thi số 6)

Bài 1: (1.5 điểm) Thực hiện các phép tính:

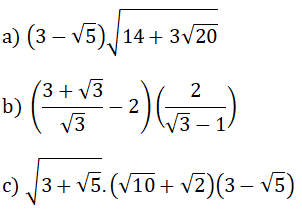
Bài 2: (1.5 điểm) Cho hàm số y = 2x + 3 có đồ thị (d₁) và hàm số y = – x có đồ thị (d₂).

a) Vẽ (d₁) và (d₂) trên cùng một mặt phẳng tọa độ.

b) Tìm tọa độ giao điểm của (d₁) và (d₂) bằng phép toán.

Bài 3: (1.5 điểm) Cho biểu thức:

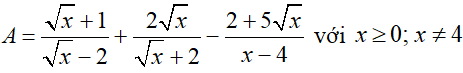
a) Thu gọn biểu thức A.

b) Tìm giá trị nhỏ nhất của A.

Bài 4: (2 điểm) Giải các phương trình:

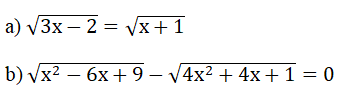
Bài 5: (3.5 điểm) Cho đường tròn (O;R) và điểm M thuộc đường tròn (O). Đường trung trực của đoạn thẳng OM cắt đường tròn (O) tại A và B và cắt OM tại H.

a) Chứng minh H là trung điểm của AB và tam giác OMA đều.

b) Chứng minh tứ giác OAMB là hình thoi.

c) Tiếp tuyến tại A của (O) cắt tia OM tại C. Chứng minh CB = CA.

d) Đường thẳng vuông góc với OA tại O cắt BC tại N. Chứng minh MN là tiếp tuyến của đường tròn (O).

Đáp án và Hướng dẫn giải

Bài 1: (1.5 điểm)

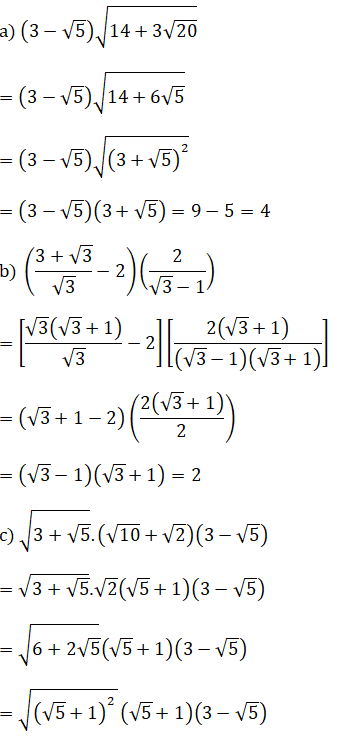
= (√5 + 1)² (3 - √5)

= (6 + 2√5)(3 - √5)

= 2(3 + √5) (3 - √5)

= 8

Bài 2: (1.5 điểm)

a) Tập xác định R

Bảng giá trị:

x	0	-1
y = 2x + 3	3	1

x	0	-1
y = - x	0	1

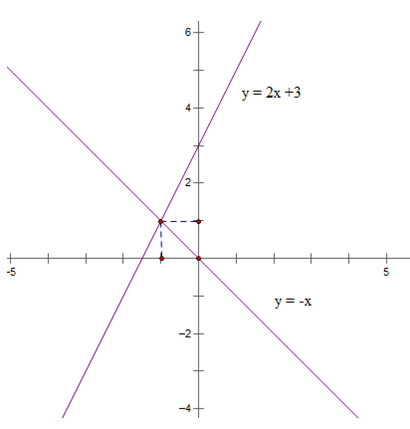
Gọi (x_o; y_o ) là tọa độ giao điểm của d₁ và d₂

Khi đó ta có:

(y_o = 2x_o + 3 và y_o = -x_o

⇒ -x_o = 2x_o + 3 ⇔ 3x_o = -3 ⇔ x_o = -1

⇒ y_o = -x_o = 1

Vậy tọa độ giao điểm của d₁ và d₂ là (- 1; 1)

Bài 3: (1.5 điểm)

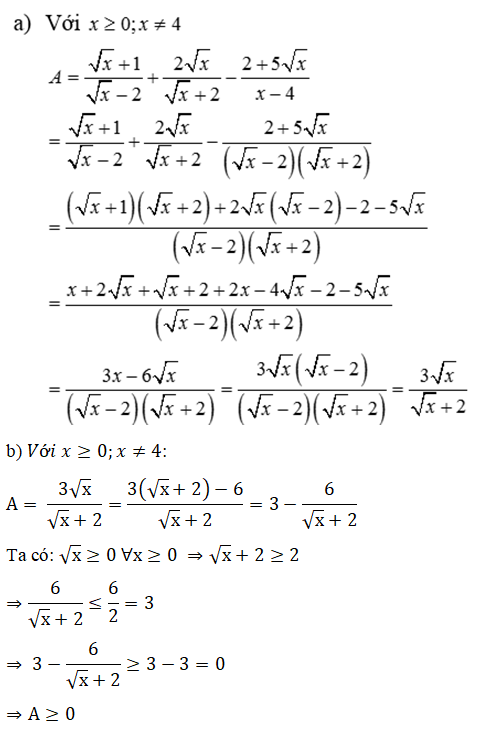
Vậy GTNN của biểu thức A là 0, đạt được khi x = 0

Bài 4: (2 điểm)

Bài 5: (3.5 điểm)

a) Chứng minh H là trung điểm của AB

Ta có OM vuông góc AB tại H (gt)

Vậy H là trung điểm của AB (đường kính vuông góc với một dây cung)

Chứng minh tam giác OAM đều:

Ta có: AM = AO (A là trung trực của OM)

và OA = OM = R

Suy ra AM = AO = OM

Vậy ΔOAM đều.

b) Chứng minh tứ giác OAMB là hình thoi.

Do H là trung điểm của AB (cmt)

H là trung điểm của OM

nên tứ giác OAMB là hình bình hành mà OM vuông góc AB.

Vậy tứ giác OAMB là hình thoi.

c) Xét ΔOAC và ΔOBC có:

OA = OB = R

∠(AOC) = ∠(BOC) (tính chất đường chéo hình thoi)

OC là cạnh chung

⇒ ΔOAC = ΔOBC (c.g.c)

⇒ AC = BC

d) Ta có: CA ⊥ OA (CA là tiếp tuyến của (O)

và ON ⊥ OA (gt)

⇒ CA // ON ⇒ ∠(CON) = ∠(ACO) (sole trong)

Mà ∠(ACO) = ∠(BCO) (ΔOAC = ΔOBC)

⇒ ∠(CON) = ∠(BCO) ⇒ ΔNCO cân tại N

Xét tam giác CAO vuông tại A có ∠(AOC) = 60^o( ΔAMO đều) nên:

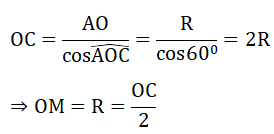
⇒ M là trung điểm của OC

ΔNCO cân tại N có NM là trung tuyến ⇒ NM cũng là đường cao

Hay NM là tiếp tuyến của (O)

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2023

Môn: Toán 9

Thời gian làm bài: 90 phút

(Đề thi số 7)

Bài 1: (1.5 điểm) Thực hiện các phép tính:

a) 4√24 - 3√54 + 5√6 - √150

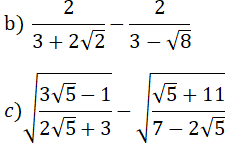
Bài 2: (1.5 điểm) Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau:

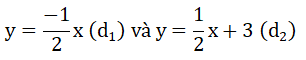
Xác định b để đường thẳng (d₃ ) y = 2x + b cắt (d₂ ) tại điểm có hoành độ và tung độ đối nhau.

Bài 3: (1.5 điểm) Giải phương trình:

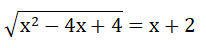
Bài 4: (2 điểm) Cho biểu thức:

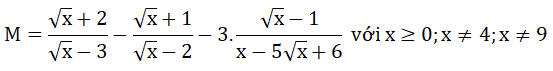
a) Thu gọn biểu thức M.

b) Tìm giá trị của x để M < – 1 .

Bài 5: (3.5 điểm) Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.

a) Chứng minh K là trung điểm của AB.

b) Tính MA, AB, OK theo R.

c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN = BH.MO .

d) Đường thẳng MO cắt đường tròn (O) tại C và D (C nằm giữa O và M). Gọi E là điểm đối xứng của C qua K. Chứng minh E là trực tâm của tam giác ABD.

Đáp án và Hướng dẫn giải

Bài 1: (1.5 điểm)

a) 4√24 - 3√54 + 5√6 - √150

= 8√6 - 9√6 + 5√6 - 5√6

= -√6

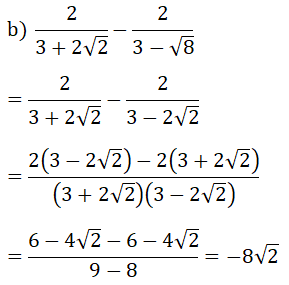
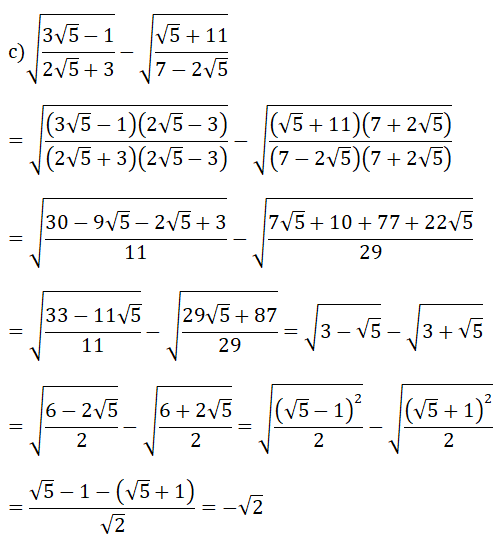
Bài 2: (1.5 điểm)

a) Tập xác định của hàm số R

Bảng giá trị

x	0	2
y = -1/2 x	0	- 1
y = 1/2 x + 3	3	4

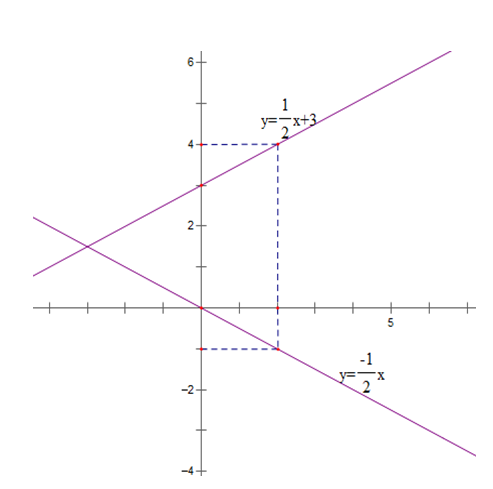
b) Gọi A (m; - m) là tọa độ giao điểm của (d₂ ) và (d₃)

Khi đó:

-m = 1/2 m + 3 ⇔ 3/2 m = 3 ⇔ m = 2

Vậy tọa độ giao điểm của d₂ và d₃ là (2; -2)

⇒ -2 = 2.2 + b ⇔ b = -6

Vậy b = - 6

Bài 3: (1.5 điểm)

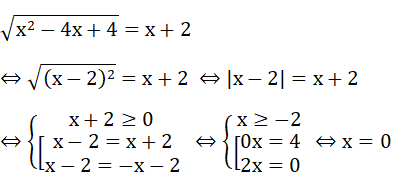
Vậy phương trình có nghiệm x = 0

Bài 4: (2 điểm)

a) Rút gọn M

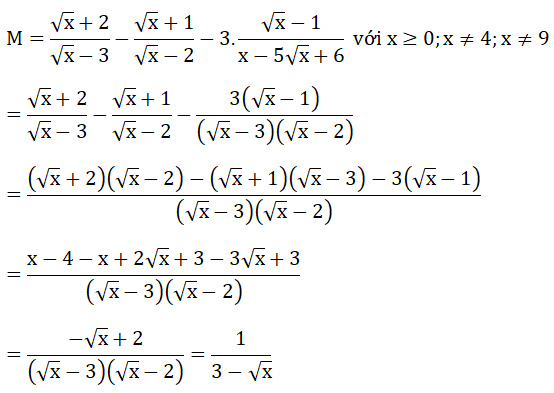
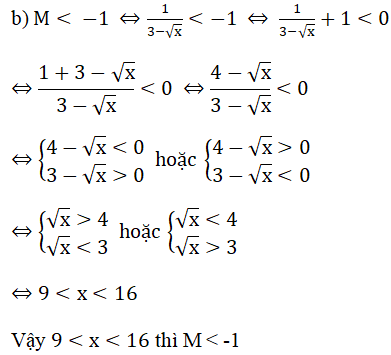
Bài 5: (3.5 điểm)

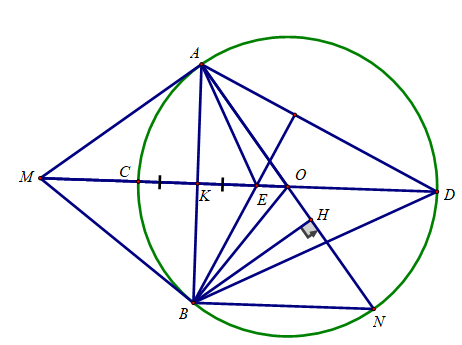
a) Ta có:

MA = MB ( tính chất 2 tiếp tuyến cắt nhau)

OA = OB ( cùng bằng bán kính đường tròn (O)

⇒ OM là đường trung trực của AB

OM ∩ AB = K ⇒ K là trung điểm của AB

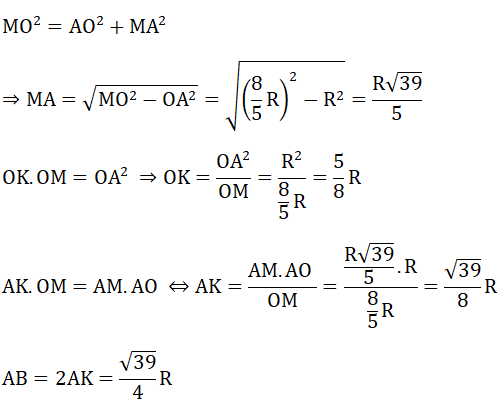
b) Tam giác MAO vuông tại A, AK là đường cao có:

c) Ta có: ∠(ABN ) = 90^o(B thuộc đường tròn đường kính AN)

⇒ BN // MO ( cùng vuông góc với AB)

Do đó:

∠(AOM) = ∠(ANB) (đồng vị))

∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))

⇒ ∠(ANB) = ∠(BOM)

Xét ΔBHN và ΔMBO có:

∠(BHN) = ∠(MBO ) = 90^o

∠(ANB) = ∠(BOM)

⇒ ΔBHN ∼ ΔMBO (g.g)

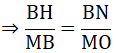
Hay MB. BN = BH. MO

d) Ta có:

K là trung điểm của CE (E đối xứng với C qua AB)

K là trung điểm của AB

AB ⊥ CE (MO ⊥ AB)

⇒ Tứ giác AEBC là hình thoi

⇒ BE // AC

Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)

Nên BE ⊥ AD và DK ⊥ AB

Vậy E là trực tâm của tam giác ADB