Cho tam giác ABC với A(1; –1), B(3; 5), C(–2; 4)

Cho tam giác ABC với A(1; –1), B(3; 5), C(–2; 4).

Sách bài tập Toán 10 Kết nối tri thức Bài tập cuối chương 7

Bài 7.55 trang 49 Sách bài tập Toán lớp 10 Tập 2: Cho tam giác ABC với A(1; –1), B(3; 5), C(–2; 4).

a) Viết phương trình tham số của đường thẳng AB.

b) Viết phương trình đường cao AH của tam giác ABC.

c) Tính khoảng cách từ điểm A đến đường thẳng BC.

d) Tính sin của góc giữa hai đường thẳng AB và AC.

Lời giải:

a)

Ta có $\overrightarrow{AB}=\left(2;6\right)$ là một vectơ chỉ phương của đường thẳng AB nên vectơ $\overrightarrow{u}=\left(1;3\right)$ cũng là một vectơ chỉ phương của AB.

Đường thẳng AB đi qua điểm A(1; –1) và nhận $\overrightarrow{u}=\left(1;3\right)$ là một vectơ chỉ phương có phương trình tham số là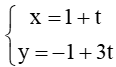

b)

Do AH vuông góc với BC nên $\overrightarrow{BC}=\left(-5;-1\right)$ là một vectơ pháp tuyến của đường cao AH.

Đường cao AH đi qua điểm A(1; –1) nhận $\overrightarrow{n}=-\overrightarrow{BC}=\left(5;1\right)$ là một vectơ pháp tuyến có phương trình tổng quát là:

5(x – 1) + 1(y + 1) = 0

⇔ 5x – 5 + y + 1 = 0

⇔ 5x + y – 4 = 0.

c)

Đường thẳng BC nhận vectơ $\overrightarrow{BC}=\left(-5;-1\right)$ là một vectơ chỉ phương nên BC nhận $\overrightarrow{n\text{'}}=\left(1;-5\right)$ là một vectơ pháp tuyến.

Do đó phương trình đường thẳng BC là:

1(x – 3) – 5(y – 5) = 0

⇔ x – 3 – 5y + 25 = 0

⇔ x – 5y + 22 = 0.

Khoảng cách từ điểm A(1; –1) đến đường thẳng BC là

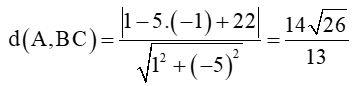
d)

Gọi α là góc giữa hai đường thẳng AB và AC có hai vectơ chỉ phương lần lượt là: $\overrightarrow{AB}=\left(2;6\right),\overrightarrow{AC}=\left(-3;5\right)$

Khi đó

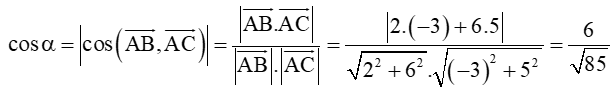
Do α là góc giữa hai đường thẳng nên sinα > 0.

Lại có sin²α + cos²α = 1.

$\Rightarrow \sin \alpha =\sqrt{1-{\cos }^2\alpha }=\frac{7}{\sqrt{85}}$