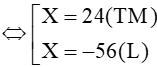Lập phương trình chính tắc của parabol (P) biết rằng, (P) đi qua điểm A(2; 4)

Lập phương trình chính tắc của parabol (P) biết rằng, (P) đi qua điểm A(2; 4). Khi đó hãy tìm điểm M thuộc (P) và cách tiêu điểm của (P) một khoảng bằng 5.

Sách bài tập Toán 10 Kết nối tri thức Bài tập cuối chương 7

Bài 7.60 trang 50 Sách bài tập Toán lớp 10 Tập 2: Lập phương trình chính tắc của parabol (P) biết rằng, (P) đi qua điểm A(2; 4). Khi đó hãy tìm điểm M thuộc (P) và cách tiêu điểm của (P) một khoảng bằng 5.

Lời giải:

Phương trình chính tắc của (P) có dạng y² = 2px.

Do (P) đi qua điểm A(2; 4) nên ta có: 4² = 2p.2 ⇔ p = 4 .

Vậy phương trình chính tắc của (P) là: y² = 8x với tiêu điểm F(2; 0).

Ta còn viết phương trình (P) dưới dạng: $x=\frac{y^2}{8}$.

Ta có:

Do điểm M thuộc (P) nên toạ độ của điểm M có dạng $M\left(\frac{t^2}{8};t\right)$

Từ giả thiết MF = 5 ta suy ra:

MF² = 25

$\iff {\left(\frac{t^2}{8}-2\right)}^2+t^2=25\iff \frac{t^2}{64}-\frac{t^2}{2}+4+t^2=25\iff \frac{t^2}{64}+\frac{t^2}{2}-21=0(*)$

Đặt t² = X (X ≥ 0) ta có:

(*) ⇔ $\frac{X^2}{64}+\frac{X}{2}-21=0$

Với X = 24 ⇔$t=\pm 2\sqrt{6}$

Vậy có hai điểm M thoả mãn là $M\left(3;\pm 2\sqrt{6}\right)$.