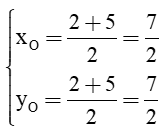Bài 6 trang 45 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10

❮ Bài trước Bài sau ❯

Cho ba điểm A(2; 2), B(3; 5), C(5; 5).

Giải Toán lớp 10 Bài 1: Toạ độ của vectơ

Bài 6 trang 45 Toán lớp 10 Tập 2: Cho ba điểm A(2; 2), B(3; 5), C(5; 5).

a) Tìm tọa độ điểm D sao cho ABCD là một hình bình hành.

b) Tìm tọa độ giao điểm hai đường chéo của một hình bình hành ABCD.

c) Giải tam giác ABC.

Lời giải:

a) Gọi D(x_D; y_D)

Ta có: $\vec{B A} = (2 - 3; 2 - 5)$ = (-1; -3); $\vec{C D} = (x_{D} - 5; y_{D} - 5)$

Để ABCD là một hình bình hành thì $\vec{B A} = \vec{C D}$

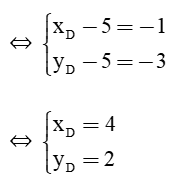
Bài 6 trang 45 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10

Vậy D(4; 2).

b) Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Suy ra O là trung điểm của AC.

Khi đó tọa độ điểm O là: Bài 6 trang 45 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10

⇒ O $(\frac{7}{2}; \frac{7}{2})$ .

Vậy O $(\frac{7}{2}; \frac{7}{2})$ .

c) Ta có: $\vec{B A}$ (-1; -3) ⇒ BA = $\sqrt{{(- 1)}^{2} + {(- 3)}^{2}} = \sqrt{10}$ .

$\vec{C A}$ (-3; -3) ⇒ CA = $\sqrt{{(- 3)}^{2} + {(- 3)}^{2}} = 3 \sqrt{2}$ .

$\vec{B C}$ (2; 0) ⇒ BC = $\sqrt{2^{2} + 0^{2}} = 2$ .

Áp dụng định lí cosin, ta có:

cosA = $\frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} = \frac{{(\sqrt{10})}^{2} + {(3 \sqrt{2})}^{2} - 2^{2}}{2. \sqrt{10} .3 \sqrt{2}} = \frac{2 \sqrt{5}}{5}$

⇒ $\hat{A}$ ≈ 26,56°

⇒ sinA = $\frac{\sqrt{5}}{5}$

Áp dụng định lí sin, ta có: $\frac{B C}{\sin A} = \frac{A B}{\sin C} = \frac{A C}{\sin B}$

$\Rightarrow \frac{2}{\frac{\sqrt{5}}{5}} = \frac{\sqrt{10}}{\sin C}$

$\Rightarrow \sin C = (\frac{\sqrt{5}}{5} . \sqrt{10}) : 2 = \frac{\sqrt{2}}{2}$ ⇒ $\hat{C}$ = 45°.

Ta lại có: $\hat{B} = 180 ° - (\hat{A} + \hat{C}) \approx 180 ° - (26, 56 ° + 45 °) \approx 108, 44 °$

Vậy BA = $\sqrt{10}$ , CA $= 3 \sqrt{2}$ , BC = 2, $\hat{A}$ ≈ 26,56°, $\hat{B} \approx 108, 44 °$ , $\hat{C}$ = 45°.

Lời giải bài tập Toán 10 Bài 1: Toạ độ của vectơ hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯