Hoạt động khám phá 6 trang 42 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10

❮ Bài trước Bài sau ❯

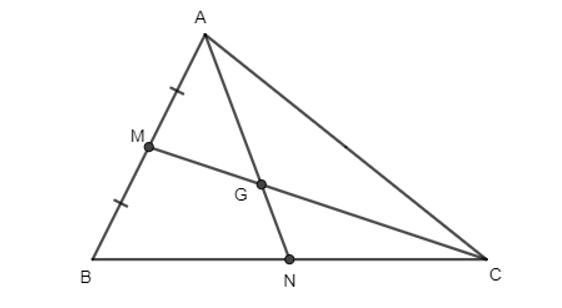
Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ ba đỉnh A(x; y), B(x; y), C(x; y). Gọi M(x; y) là trung điểm của đoạn thẳng AB, G(x; y) là trọng tâm của tam giác ABC.

Giải Toán lớp 10 Bài 1: Toạ độ của vectơ

Hoạt động khám phá 6 trang 42 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ ba đỉnh A(x_A; y_A), B(x_B; y_B), C(x_C; y_C). Gọi M(x_M; y_M) là trung điểm của đoạn thẳng AB, G(x_G; y_G) là trọng tâm của tam giác ABC.

a) Biểu thị vectơ $\vec{O M}$ theo hai vectơ $\vec{O A}$ và $\vec{O B}$ .

b) Biểu thị vectơ $\vec{O G}$ theo hai vectơ $\vec{O A}$ , $\vec{O B}$ và $\vec{O C}$ .

c) Từ các kết quả trên, tìm tọa độ điểm M và G theo tọa độ của các điểm A, B, C.

Lời giải:

Hoạt động khám phá 6 trang 42 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10

Vì M là trung điểm của AB nên ta có: $\vec{O A} + \vec{O B} = 2 \vec{O M}$

⇔ $\vec{O M} = \frac{1}{2} \vec{O A} + \frac{1}{2} \vec{O B}$ .

b) Ta có

$\vec{O A} + \vec{O B} + \vec{O C} = \vec{O G} + \vec{G A} + \vec{O G} + \vec{G B} + \vec{O G} + \vec{G C} = 3 \vec{O G} + (\vec{G A} + \vec{G B} + \vec{G C})$

Mà $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

Do đó $\vec{O A} + \vec{O B} + \vec{O C} = 3 \vec{O G}$

Hay $\vec{O G} = \frac{1}{3} \vec{O A} + \frac{1}{3} \vec{O B} + \frac{1}{3} \vec{O C}$

c) Tọa độ của $\vec{O M}$ là tọa độ của điểm M nên $\vec{O M}$ = (x_M; y_M);

Tọa độ của $\vec{O A}$ là tọa độ của điểm A nên $\vec{O A}$ = (x_A; y_A);

Tọa độ của $\vec{O B}$ là tọa độ của điểm B nên $\vec{O B}$ = (x_B; y_B);

Vì $\vec{O M} = \frac{1}{2} \vec{O A} + \frac{1}{2} \vec{O B}$ nên ta có $x_{M} = \frac{x_{A} + x_{B}}{2}, y_{M} = \frac{y_{A} + y_{B}}{2}$ .

Vậy $M (\frac{x_{A} + x_{B}}{2}; \frac{y_{A} + y_{B}}{2})$ .

Tọa độ của $\vec{O G}$ là tọa độ của điểm G nên $\vec{O G}$ = (x_G; y_G);

Tọa độ của $\vec{O A}$ là tọa độ của điểm A nên $\vec{O A}$ = (x_A; y_A);

Tọa độ của $\vec{O B}$ là tọa độ của điểm B nên $\vec{O B}$ = (x_B; y_B);

Tọa độ của $\vec{O C}$ là tọa độ của điểm C nên $\vec{O C}$ = (x_C; y_C);

Vì $\vec{O G} = \frac{1}{3} \vec{O A} + \frac{1}{3} \vec{O B} + \frac{1}{3} \vec{O C}$ nên ta có $x_{G} = \frac{x_{A} + x_{B} + x_{C}}{3}, y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3}$ .

Vậy $G (\frac{x_{A} + x_{B} + x_{C}}{3}; \frac{y_{A} + y_{B} + y_{C}}{3})$ .

Lời giải bài tập Toán 10 Bài 1: Toạ độ của vectơ hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯