Tóm tắt Lý thuyết Toán lớp 6 Chương 3: Hình học trực quan và hình phẳng | Chân trời sáng tạo
Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 6 Chương 3: Hình học trực quan và hình phẳng hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.
Toán lớp 6 Chương 3: Hình học trực quan và hình phẳng - Lý thuyết chi tiết
Lý thuyết Toán 6 Bài 1: Hình vuông - Tam giác đều - Lục giác đều
Lý thuyết Toán 6 Bài 2: Hình chữ nhật - Hình thoi - Hình bình hành - Hình thang cân
Lý thuyết Toán 6 Bài 3: Chu vi và diện tích của một số hình trong thực tiễn
Lý thuyết Toán 6 Bài 1: Hình vuông - Tam giác đều - Lục giác đều
A. Lý thuyết
1. Hình vuông
Hình vuông có:
+ Bốn đỉnh.
+ Bốn cạnh bằng nhau.
+ Bốn góc bằng nhau và bằng góc vuông.
+ Hai đường chéo của hình vuông bằng nhau.
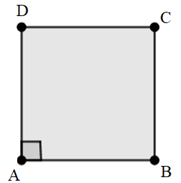
Ví dụ:
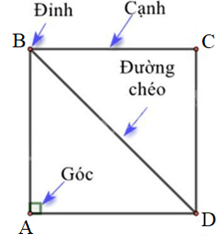
- Bốn đỉnh A, B, C, D.
- Bốn cạnh bằng nhau: AB = BC = CD = DA.
- Bốn góc ở các đỉnh A, B, C, D là góc vuông.
- Hai đường chéo bằng nhau: AC = BD.
Cách vẽ hình vuông
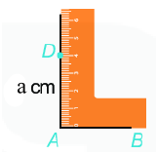
Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh bằng a (cm).
Bước 1: Vẽ đoạn thẳng AB = a (cm).
Bước 2: Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = a (cm).
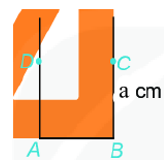
Bước 3: Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = a (cm).
Bước 4: Nối C với D ta được hình vuông ABCD.
2. Tam giác đều
Tam giác đều có:
+ Ba đỉnh.
+ Ba cạnh bằng nhau.
+ Ba góc ở ba đỉnh bằng nhau.
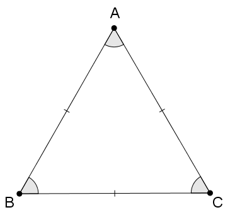
Ví dụ:
Tam giác đều ABC có:
- Ba đỉnh A, B, C.
- Ba cạnh bằng nhau: AB = BC = CA.
- Ba góc đỉnh A, B, C bằng nhau.
Cách vẽ tam giác đều
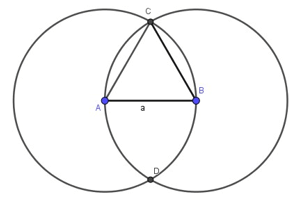
Cách vẽ tam giác đều cạnh a (cm) bằng thước và compa:
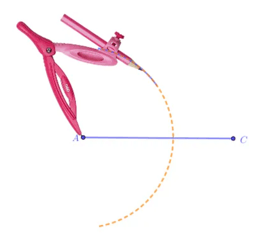
Bước 1: Dùng thước vẽ đoạn thẳng AB = a (cm).
Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.
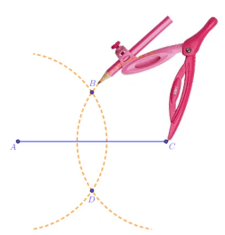
Bước 3: Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.
Bước 4: Dùng thước vẽ các đoạn thẳng AC và BC.
Ta được tam giác ABC đều cạnh a (như hình vẽ).
3. Lục giác đều
Hình lục giác đều có sáu đỉnh, sáu cạnh bằng nhau, sáu góc ở các đỉnh bằng nhau, ba đường chéo chính bằng nhau.
Ví dụ:
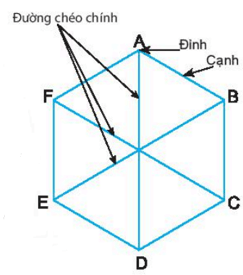
Lục giác đều ABCDEF có:
- Sáu đỉnh A, B, C, D, E, F.
- Sáu cạnh bằng nhau: AB = BC = CD = DE = EF.
- Sáu góc đỉnh A, B, C, D, E, F bằng nhau.
- Ba đường chéo chính bằng nhau AD = BE = CF.
B. Bài tập tự luyện
Bài 1. Dùng thước và êke để vẽ hình vuông cạnh 8 cm. Kẻ thêm hai đường chéo rồi dùng compa đo và so sánh độ dài của chúng.
Hướng dẫn giải
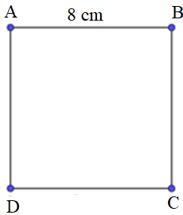
* Vẽ hình vuông cạnh 8 cm.
- Vẽ cạnh AB = 8 cm.
- Vẽ đường thẳng qua A vuông góc với AB. Trên đường thẳng này lấy điểm D sao cho AD = 8 cm.
- Vẽ đường thẳng qua B vuông góc với AB. Trên đường thẳng này lấy điểm C sao cho BC = 7cm.
- Nối C với D ta được hình vuông ABCD.
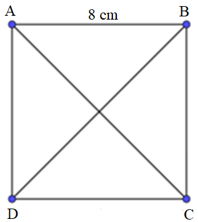
* Đo và so sánh độ dài hai đường chéo của hình vuông ABCD.
- Nối A với C, B với D. Khi đó, AC và BD là hai đường chéo của hình vuông ABCD.
- Mở compa một đoạn bằng AC và giữ nguyên compa.
- Đặt một đầu của compa trùng với một trong hai điểm của đoạn thẳng BD, ta thấy điểm còn lại trùng với đầu kia của compa.
Do đó hai đường chéo của hình vuông ABCD bằng nhau.
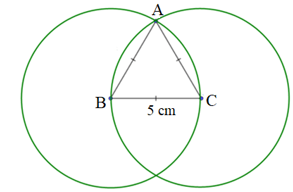
Bài 2. Dùng thước và compa để vẽ hình tam giác đều cạnh 5 cm.
Hướng dẫn giải
Bước 1: Vẽ đoạn thẳng BC = 5 cm.
Bước 2: Vẽ đường tròn tâm C bán kính 5 cm và đường tròn tâm B bán kính 5 cm.
Bước 3: Gọi A là một trong hai giao điểm của đường tròn.
Khi đó ta có: AB = AC = BC = 5 cm, các góc của tam giác ABC bằng nhau.
Ta được tam giác đều ABC cạnh 5 cm.
Lý thuyết Toán 6 Bài 2: Hình chữ nhật - Hình thoi - Hình bình hành - Hình thang cân
A. Lý thuyết
1. Hình chữ nhật
Hình chữ nhật có:
+ Bốn đỉnh.
+ Hai cặp cạnh đối diện bằng nhau.
+ Hai cặp cạnh đối diện song song.
+ Bốn góc ở các đỉnh bằng nhau và bằng góc vuông.
+ Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Ví dụ:
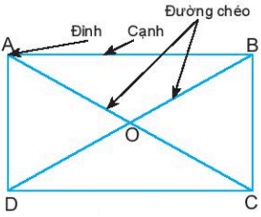
Hình chữ nhật ABCD có:
- Bốn đỉnh A, B, C, D.
- Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường:
AC = BD và OA = OC; OB = OD.
Cách vẽ hình chữ nhật
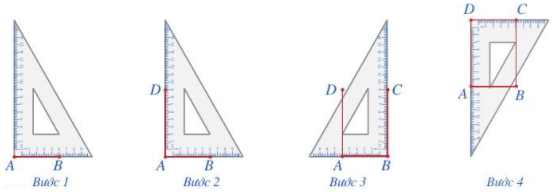
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 6 cm.
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 9 cm.
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 9 cm.
Bước 4. Vẽ đoạn thẳng CD. Ta được hình chữ nhật ABCD.
2. Hình thoi
Hình thoi có:
+ Bốn đỉnh.
+ Bốn cạnh bằng nhau.
+ Hai cặp cạnh đối diện song song với nhau.
+ Hai đường chéo vuông góc với nhau.
Ví dụ:
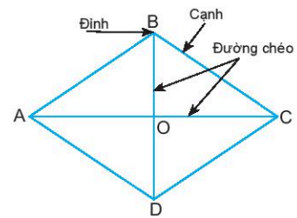
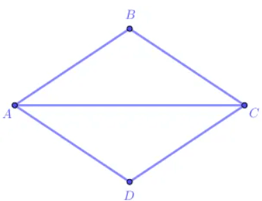
Hình thoi ABCD có:
- Bốn đỉnh A, B, C, D.
- Bốn cạnh bằng nhau: AB = BC = CD = DA;
- Hai cạnh đối AB và CD, AD và BC song song với nhau.
- Hai đường chéo AC và BD vuông góc với nhau.
Cách vẽ hình thoi
Ví dụ: Dùng thước và compa vẽ hình thoi ABCD, biết AB = 5 cm và AC = 8 cm.
Hướng dẫn giải
Bước 1. Dùng thước vẽ đoạn thẳng AC = 8 cm.
Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính 5 cm.
Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính 5cm; phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.
Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA. Ta được hình thoi ABCD (như hình vẽ).
3. Hình bình hành
Hình bình hành có:
+ Bốn đỉnh.
+ Hai cặp cạnh đối diện bằng nhau.
+ Hai cặp cạnh đối diện song song.
+ Hai cặp góc đối diện bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Ví dụ:
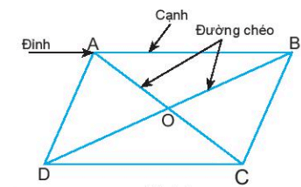
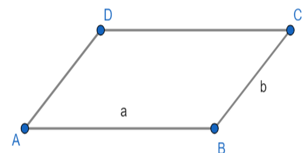
Hình bình hành ABCD có:
- Bốn đỉnh A, B, C, D.
- Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Hai cặp góc đối diện bằng nhau: góc đỉnh A bằng góc đỉnh C; góc đỉnh B bằng góc đỉnh D.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: OA = OC; OB = OD.
Cách vẽ hình bình hành
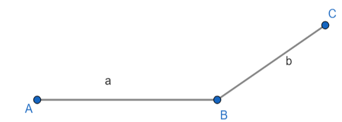
Hình bình hành ABCD có hai cạnh là a và b.
Bước 1: Vẽ đoạn thẳng AB = a (cm).
Bước 2: Vẽ đường thẳng đi qua B. Lấy điểm C trên đường thẳng đó sao cho BC = b (cm).
Bước 3: Vẽ đường thẳng đi qua A và song song với cạnh BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.
4. Hình thang cân
Hình thang cân có:
+ Hai cạnh đáy song song.
+ Hai cạnh bên bằng nhau.
+ Hai góc kề một đáy bằng nhau.
+ Hai đường chéo bằng nhau.
Ví dụ:
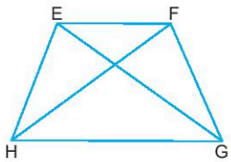
Hình thang cân EFGH có:
- Hai cạnh đáy song song: EF song song với GH.
- Hai cạnh bên bằng nhau: EH = FG.
- Hai góc kề một đáy bằng nhau: góc đỉnh E bằng góc đỉnh F, góc đỉnh G bằng góc đỉnh H.
- Hai đường chéo bằng nhau: EG = FH.
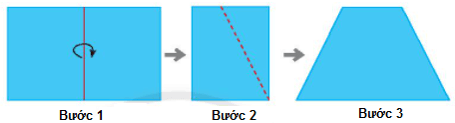
Cách gấp hình thang cân
Bước 1: Gấp đôi một tờ giấy hình chữ nhật.
Bước 2: Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh đối diện (cạnh không chứa nếp gấp). Cắt theo đường nét đứt như hình minh họa.
Bước 3: Mở tờ giấy ra ta được một hình thang cân.
....................................
....................................
....................................