Tóm tắt Lý thuyết Toán lớp 6 Chương 8: Hình học phẳng và các hình học cơ bản | Lý thuyết Toán lớp 6 Chân trời sáng tạo
Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 6 Chương 8: Hình học phẳng và các hình học cơ bản hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.
Toán lớp 6 Chương 8: Hình học phẳng và các hình học cơ bản - Lý thuyết chi tiết
- Lý thuyết Toán 6 Bài 1: Điểm. Đường thẳng
- Lý thuyết Toán 6 Bài 2: Ba điểm thẳng hàng. Ba điểm không thẳng
- Lý thuyết Toán 6 Bài 3: Hai đường thẳng cắt nhau, song song. Tia
- Lý thuyết Toán 6 Bài 4: Đoạn thẳng. Độ dài đoạn thẳng
- Lý thuyết Toán 6 Bài 5: Trung điểm của đoạn thẳng
- Lý thuyết Toán 6 Bài 6: Góc
- Lý thuyết Toán 6 Bài 7: Số đo góc. Các góc đặc biệt
- Tổng hợp lý thuyết Toán lớp 6 Chương 8
Lý thuyết Toán 6 Bài 1: Điểm. Đường thẳng
A. Lý thuyết
1. Điểm
Mỗi chấm nhỏ trên trang giấy, trên bảng, … cho ta hình ảnh của một điểm.
Người ta thường dùng các chữ cái in hoa A, B, C, D, …. để đặt tên cho điểm.
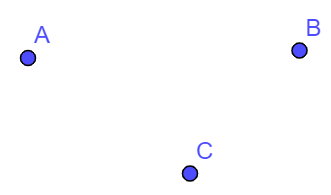
Ví dụ 1. Hình vẽ bên dưới là hình vẽ các điểm A, B, C.
Chú ý:
- Khi nói tới hai điểm mà không giải thích gì thêm, ta coi đó là hai điểm phân biệt.
- Từ những điểm, ta xây dựng được các hình. Mỗi hình là một tập hợp các điểm. Một điểm cũng được coi là một hình.
Ví dụ 2. Hai điểm M và N là hai điểm phân biệt (như hình vẽ).

2. Đường thẳng
Dùng bút kẻ một vạch thẳng dọc theo mép thước ta sẽ được hình ảnh của một đường thẳng.
Chú ý: Ta thường dùng các chữ cái in hoa a, b, c, d, …. để đặt tên các đường thẳng.
Ví dụ 3. Hình vẽ bên dưới là hình vẽ đường thẳng a.

3. Vẽ đường thẳng
Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
Ví dụ 4. Từ hai điểm A, B cho trước. Có một và một đường thẳng đi qua hai điểm A và B (đường thẳng a) như hình vẽ.

4. Điểm thuộc đường thẳng. Điểm không thuộc đường thẳng
- Vẽ một điểm A trên giấy, dùng thước thẳng vẽ đường thẳng d đi qua điểm A. Khi đó, ta nói điểm A thuộc đường thẳng d (hoặc đường thẳng d chứa điểm A), hoặc điểm A nằm trên đường thẳng d), kí hiệu là: A∈d (như hình vẽ).

- Dùng thước thẳng vẽ đường thẳng d không đi qua điểm B.
Khi đó, ta nói điểm B không thuộc đường thẳng d (hoặc đường thẳng d không chứa điểm B hoặc điểm B không nằm trên đường thẳng d), kí hiệu là: B∉ d(như hình vẽ).

Chú ý: Nếu trên đường thẳng a có hai điểm A và B, ta cũng có thể gọi tên đường thẳng đó là đường thẳng AB hay BA (như hình vẽ).

B. Bài tập tự luyện
Bài 1.
a) Hãy đặt tên cho các điểm và đường thẳng trong hình dưới đây.
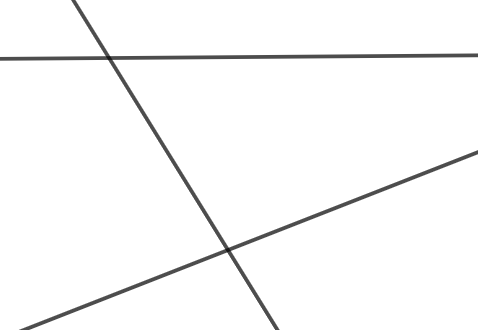
b) Hãy nêu ba cách gọi tên đường thẳng trong hình dưới đây.

Lời giải:
a) Đường thẳng được đặt tên bởi chữ in thường như: a, b, c, x, y, …
Điểm được đặt tên bởi chữ in hoa: A, B, C, D, …
Chẳng hạn: ta đặt tên các điểm là A, B và các đường thẳng là a, b, c (như hình vẽ).
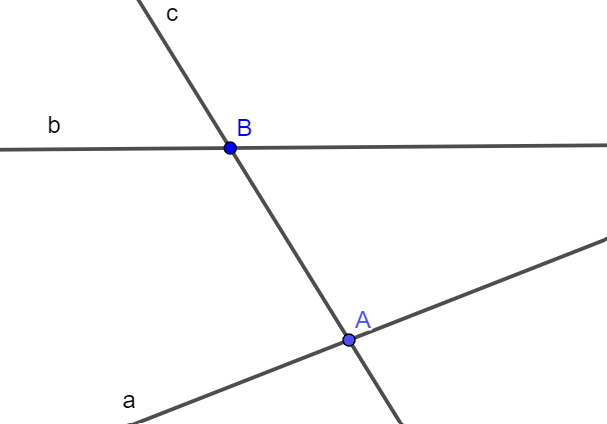
b) Ta có thể gọi tên đường thẳng bằng cách:
- Gọi theo tên đường thẳng, thường được đặt bằng chữ cái thường a, b, c, …
- Gọi tên bằng hai điểm thuộc đường thẳng.
Ba cách gọi tên đường thẳng trong hình trên là: đường thẳng AB, đường thẳng BC và đường thẳng AC.
Bài 2. Dùng kí hiệu để biểu thị các mối quan hệ dưới đây và vẽ các hình tương ứng.
a) Các điểm M, N thuộc đường thẳng a.
b) Các điểm P, Q không thuộc đường thẳng b.
Lời giải:
a) Điểm thuộc đường thẳng ta dùng kí hiệu: ∈.
- Điểm A thuộc đường thẳng p. Ký hiệu: M∈a.
- Điểm B thuộc đường thẳng. Ký hiệu: N∈a.
Ta có hình vẽ:

b) Điểm không thuộc đường thẳng ta dùng kí hiệu: ∉.
- Điểm C không thuộc đường thẳng b. Ký hiệu: P∉ b.
- Điểm D không thuộc đường thẳng b. Ký hiệu: Q∉ b.
Ta có hình vẽ:

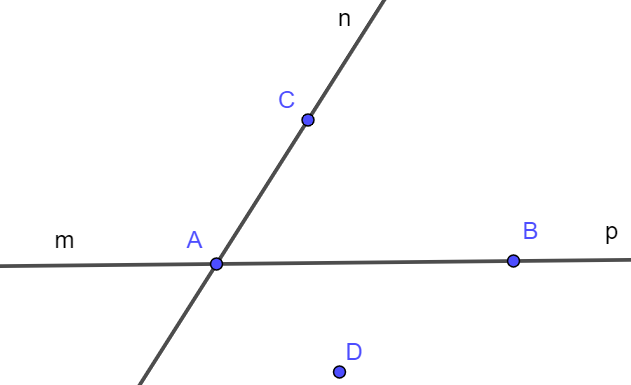
Bài 3. Trong hình vẽ bên:
a) Điểm A thuộc những đường thẳng nào?
b) Điểm B thuộc đường thẳng nào và không thuộc những đường thẳng nào?
c) Đường thẳng nào chứa điểm C?
d) Đường thẳng nào không chứa điểm D?
Sử dụng kí hiệu để mô tả các quan hệ trên.
Lời giải:
a) Điểm thuộc đường thẳng ta dùng kí hiệu: ∈.
Trong hình vẽ trên, điểm A thuộc các đường thẳng: m, n và p.
Ký hiệu: A∈ m, A∈ n, A∈ p.
b) Điểm không thuộc đường thẳng ta dùng kí hiệu: ∉.
Trong hình vẽ trên, điểm B thuộc đường thẳng p. Ký hiệu: B∈ p.
Điểm B không thuộc đường thẳng m và n.
Ký hiệu: B∉ m, B∉ n.
c) Trong hình vẽ trên, đường thẳng chứa điểm C là m và p. Hay điểm C thuộc hai đường thẳng m và p.
Ký hiệu: C∈ m, C∈ p.
d) Đường thẳng nào không chứa điểm D là m, n và p. Hay điểm D không thuộc đường thẳng m, n và p.
Kí hiệu: D∉ m, D∉ n, D∉ p.
Lý thuyết Toán 6 Bài 2: Ba điểm thẳng hàng. Ba điểm không thẳng
A. Lý thuyết
1. Ba điểm thẳng hàng
- Ba điểm phân biệt A, B, C cùng thuộc một đường thẳng được gọi là ba điểm thẳng hàng.
Ta có hình vẽ:

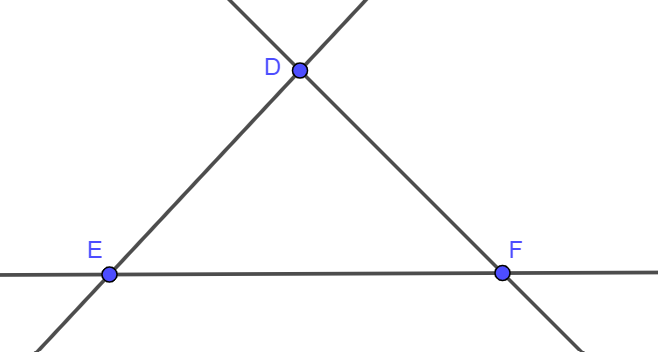
- Ba điểm D, E, F không cùng thuộc bất kì một đường thẳng nào được gọi là ba điểm không thẳng hàng.
Ta có hình vẽ:
2. Quan hệ giữa ba điểm thẳng hàng
Trong ba điểm thẳng hàng, có một và chỉ một điểm nằm giữa hai điểm còn lại.
Ví dụ 1. Với ba điểm A, B, C thẳng hàng. Điểm B nằm giữa hai điểm còn lại (như hình vẽ).

Trong hình vẽ trên:
- Các điểm B và C nằm cùng phía đối điểm A;
- Các điểm A và C nằm khác phía đối với điểm B.
B. Bài tập tự luyện
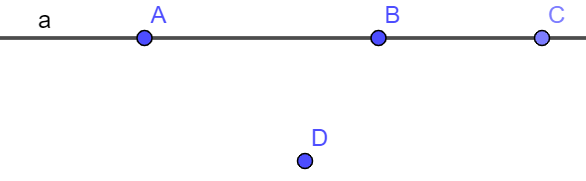
Bài 1. Cho hình vẽ sau. Hãy nêu các bộ ba điểm thẳng hàng và bộ ba điểm không thẳng hàng.
Lời giải:
Trong hình vẽ trên, ba điểm A, B, C đều thuộc đường thẳng a và điểm D không thuộc đường thẳng a.
Vậy bộ ba điểm thẳng hàng: (A, B, C);
Các bộ ba điểm không thẳng hàng: (A, B, D); (A, C, D); (B, C, D).
Bài 2. Cho hai điểm E và F. Vẽ hình theo các diễn đạt sau:
a) Lấy điểm G sao cho ba điểm E, F, G thẳng hàng và E, F nằm cùng phía đối với điểm G.
b) Lấy điểm H sao cho ba điểm E, F, H thẳng hàng và E, F nằm khác phía đối với điểm H.
Lời giải:
- Lấy hai điểm điểm E, F bất kỳ (hai điểm E và F phân biệt).
- Vẽ đường thẳng đi qua hai điểm E và F.
Ta có đường thẳng EF (như hình vẽ).

a) Trên đường thẳng EF lấy điểm G sao cho hai điểm E và F nằm cùng phía đối với điểm G. Ta có hai trường hợp sau:
- Trường hợp 1: Điểm G nằm bên trái điểm E (như hình vẽ).

- Trường hợp 2: Điểm G nằm bên phải điểm F (như hình vẽ).

b) Trên đường thẳng EF lấy điểm H sao cho hai điểm E và F nằm khác phía đối với điểm H. Hay điểm H nằm giữa hai điểm E và F.

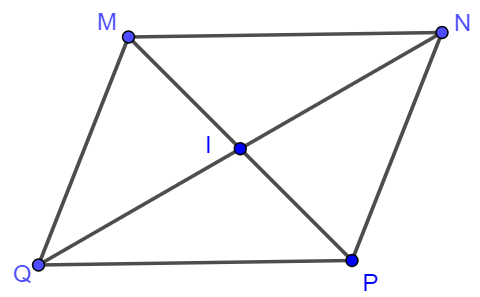
Bài 3. Cho hình bình hành MNPQ. Hãy xác định điểm O sao cho các bộ ba điểm M, I, P và N, I, Q đều là các bộ ba điểm thẳng hàng.
Lời giải:
Ba điểm M, I, P thẳng hàng nên I thuộc đường thẳng MP.
Ba điểm N, I, Q thẳng hàng nên I thuộc đường thẳng NQ.
Do đó I là giao điểm của đường thẳng MP và đường thẳng NQ.
Điểm I thỏa mãn điều kiện các bộ ba điểm M, I, P và N, I, Q đều là các bộ ba điểm thẳng hàng có thể xác định như hình vẽ sau.