Lý thuyết Toán 8 Cánh diều Bài 1: Hình chóp tam giác đều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 8 Bài 1: Hình chóp tam giác đều sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết Toán 8 Cánh diều Bài 1: Hình chóp tam giác đều

A. Lý thuyết

1. Hình chóp tam giác đều

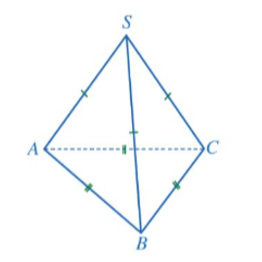
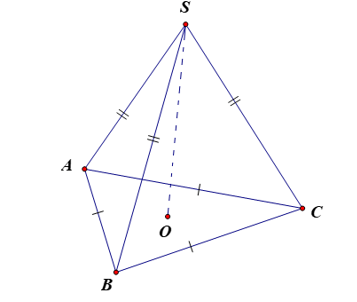
- Hình chóp tam giác đều S.ABC;

- Mặt đáy ABC là một tam giác đều;

- Các mặt bên SAB, SBC, SCA là những tam giác cân tại S;

- Các cạnh đáy AB, BC, CA bằng nhau;

- Các cạnh bên SA, SB, SC bằng nhau;

- S gọi là đỉnh của hình chóp tam giác đều S.ABC.

Chú ý:

Hình chóp tam giác đều có 4 mặt, 6 cạnh.

2. Diện tích xung quanh của hình chóp tam giác đều

2.1. Trung đoạn của hình chóp tam giác đều

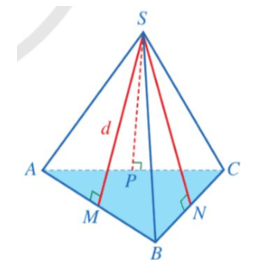
Cho hình chóp tam giác đều S.ABC. Gọi SM, SN, SP lần lượt là đường cao của các tam giác SAB, SBC, SCA. Mỗi đoạn thẳng SM, SN, SP đều được gọi là trung đoạn của hình chóp tam giác đều S.ABC.

2.2. Công thức tính diện tích xung quanh của hình chóp tam giác đều

Công thức tính

Diện tích xung quanh của hình chóp tam giác đều bằng nửa tích của chu vi đáy với độ dài trung đoạn.

Tức là:

$S_{xq}=\frac{1}{2}.C.d$, trong đó S_xq là diện tích xung quanh, C là chu vi đáy, d là độ dài trung đoạn của hình chóp tam giác đều.

Ví dụ:

Cho hình chóp tam giác đều có độ dài cạnh đáy bằng 5cm và độ dài trung đoạn bằng 8cm. Tính diện tích xung quanh của hình chóp tam giác đều đó?

Hướng dẫn giải

Chu vi đáy của hình chóp tam giác đều là: 5 + 5 + 5 = 15 (cm).

Diện tích xung quanh của hình chóp tam giác đều đó là:

$S_{xq}=\frac{1}{2}\mathrm{.15.8}=60$ (cm²)

Vậy diện tích xung quanh của hình chóp tam giác đều là 60 cm².

3. Thể tích của hình chóp tam giác đều

Cách tính

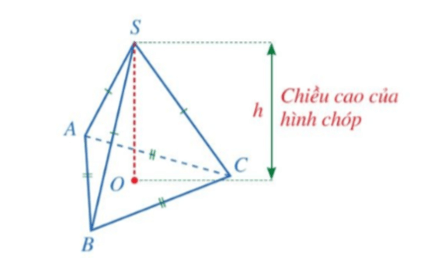
Thể tích của hình chóp tam giác đều bằng một phần ba tích của diện tích đáy với chiều cao.

Tức là:

$V=\frac{1}{3}.S.h$, trong đó V là thể tích, S là diện tích đáy, h là chiều cao của hình chóp tam giác đều.

Ví dụ:

Một khối rubik có dạng hình chóp tam giác đều với diện tích đáy khoảng 22,45 cm² và chiều cao khoảng 5,88 cm. Tính thể tích khối rubik đó?

Hướng dẫn giải

Thể tích của khối rubik đó là: $V\approx \frac{1}{3}.22,45.5,88=44,002$  (cm³).

Vậy thể tích khối rubik là: 44,002 cm³.

B. Bài tập vận dụng

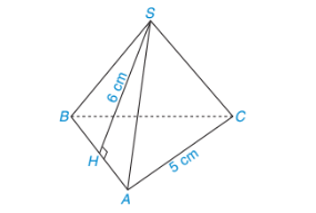
Bài 1: Tính diện tích xung quanh của hình chóp đều S.ABC như hình vẽ bên dưới

Hướng dẫn giải

Nửa chu vi đáy của hình chóp tam giác đều là: $\frac{1}{2}.\left(5+5+5\right)=\frac{15}{2}$  (cm).

Trung đoạn của hình chóp tam giác đều là: d = SH = 6 cm.

Diện tích xung quanh của hình chóp tam giác đều là: $S_{xq}=\frac{15}{2}.6=45$  (cm²).

Vậy diện tích xung quanh của hình chóp tam giác đều là 45 cm².

Bài 2: Một hình chóp tam giác đều S.ABC có diện tích đáy ABC là 27 cm² và chiều cao SO là 8cm. Tính thể tích của hình chóp tam giác đều S.ABC?

Hướng dẫn giải

Thể tích của hình chóp tam giác đều đó là: $V=\frac{1}{3}.27.8=72$  (cm³).

Vậy thể tích của hình chóp tam giác đều đó là 72 cm³.

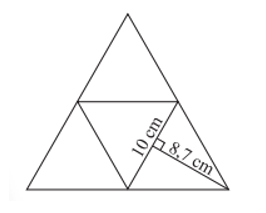
Bài 3: Nhân dịp tết trung thu, Nam dự định làm một chiếc lồng đèn hình chóp tam giác đều. Chiếc đèn lồng được làm bằng một tấm bìa như hình bên dưới biết rằng các mặt đều là hình tam giác đều. Em hãy giúp Nam tính xem phải cần bao nhiêu mét vuông giấy vừa đủ để dán tất cả các mặt của chiếc đèn lồng. Biết rằng nếp gấp không đáng kể? (lấy $\sqrt{3}\approx 1,7$ ).

Hướng dẫn giải

Chu vi đáy của chiếc đèn lồng là: 10.3 = 30 (cm).

Diện tích xung quanh của chiếc đèn lồng là: $S_{xq}=\frac{1}{2}.30.8,7=130,5$  (cm²).

Diện tích mặt đáy của chiếc đèn lồng là: $S={10}^2.\frac{\sqrt{3}}{4}\approx 42,5$  (cm²).

Diện tích giấy dán chiếc đèn lồng là: 130,5 + 42,5 = 173 (cm²).

Vậy diện tích giấy dán chiếc đèn lồng là 173 cm².