Lý thuyết Toán 8 Cánh diều Bài 2: Tứ giác

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 8 Bài 2: Tứ giác sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết Toán 8 Cánh diều Bài 2: Tứ giác

A. Lý thuyết

1. Tứ giác

1.1. Nhận biết tứ giác

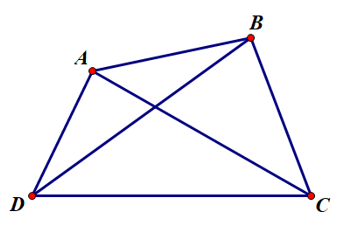
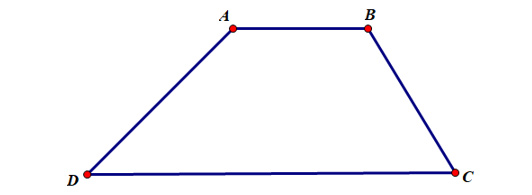
Trong tứ giác ABCD:

- Hai cạnh kề nhau (chẳng hạn: AB, BC) không cùng thuộc một đường thẳng;

- Không có ba đỉnh nào thẳng hàng;

- Có thể đọc tên góc theo tên đỉnh, chẳng hạn, góc ABC còn gọi là góc B và góc đó còn gọi là góc trong của tứ giác.

Nhận xét:

Tứ giác có 4 cạnh, 2 đường chéo, 4 đỉnh và 4 góc.

Ví dụ: Kể ra các cạnh, đường chéo, đỉnh và góc trong hình vẽ.

Hướng dẫn giải

Tứ giác ABCD có:

- Các cạnh: AB, BC, CD, DA;

- Các cặp cạnh đối: AB và CD, BC và DA;

- Các đường chéo: AC, BD;

- Các đỉnh: A, B, C, D;

- Các góc: $\widehat{DAB},\widehat{ABC},\widehat{BCD},\widehat{CDA}$ ;

- Các cặp góc đối: $\widehat{BAD}$  và $\widehat{BCD}$ ; $\widehat{ABC}$  và $\widehat{ADC}$ .

1.2. Nhận biết tứ giác lồi

Định nghĩa: Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó.

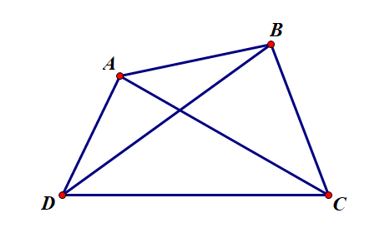
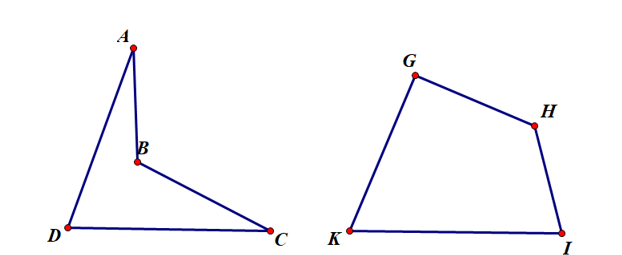
Ví dụ: Cho hai hình vẽ, tứ giác nào là tứ giác lồi? Đọc tên các cạnh, các đỉnh, các góc của tứ giác đó.

Hướng dẫn giải

Tứ giác GHIK luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó nên tứ giác GHIK là tứ giác lồi.

Tứ giác GHIK có:

• Các cạnh là: GH, HI, IK, KG;

• Các đỉnh là: G, H, I, K;

• Các góc là: $\widehat{G},\widehat{H},\widehat{I},\widehat{K}$ .

Quy ước: Từ nay về sau, khi nói về tứ giác mà không có ghi chú gì thêm thì ta hiểu đó là tứ giác lồi.

2. Tổng các góc của một tứ giác

Định lí: Tổng các góc của một tứ giác bằng 360°.

Ví dụ: Tứ giác ABCD có số đo của $\widehat{A},\widehat{B},\widehat{C},\widehat{D}$  lần lượt là x, 2x, 3x và 4x. Tính số đo mỗi góc của tứ giác ABCD.

Hướng dẫn giải

Trong tứ giác ABCD, ta có:

$BF=CF=\frac{1}{2}BC.$

Do đó: x + 2x + 3x + 4x = 360° hay 10x = 360°. Suy ra x = 36°.

Vậy tứ giác ABCD có:

 $\widehat{A}=36°;\widehat{B}=2x=72°;\widehat{C}=3x=108°;\widehat{D}=4x=144°$ .

B. Bài tập tự luyện

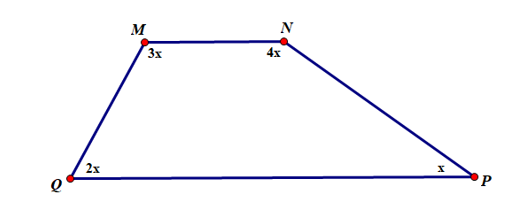
Bài 1. Cho hình vẽ. Tìm x.

Hướng dẫn giải

Áp dụng tính chất về góc vào tứ giác MNPQ, ta có:

$\widehat{M}+\widehat{N}+\widehat{P}+\widehat{Q}=360°$

Hay 3x + 4x + x + 2x = 360°

Suy ra 10x = 360° hay x = 36°.

Vậy x = 36°.

Bài 2. Cho tứ giác ABCD có $\widehat{A}:\widehat{B}:\widehat{C}:\widehat{D}=6:5:4:3$ . Tính các góc của tứ giác ABCD.

Hướng dẫn giải

Tứ giác ABCD có $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$

Mặt khác , theo tính chất dãy tỷ số bằng nhau ta có:

$\frac{\widehat{\text{A}}}{6}+\frac{\widehat{\text{B}}}{5}+\frac{\widehat{\text{C}}}{4}+\frac{\widehat{\text{D}}}{3}=\frac{\widehat{\text{A}}+\widehat{\text{B}}+\widehat{\text{C}}+\widehat{\text{D}}}{6+5+4+3}=\frac{360°}{18}=20°$

Suy ra $\widehat{A}=20°.6=120°$ ; $\widehat{\text{B}}\text{ = 20°. 5 = 100°}$ ;

$\widehat{C}=20°.4=80°$; $\widehat{D}=20°.3=60°$ .

Vậy $\widehat{A}=120°;\widehat{B}=100°;\widehat{C}=80°;\widehat{D}=60°.$

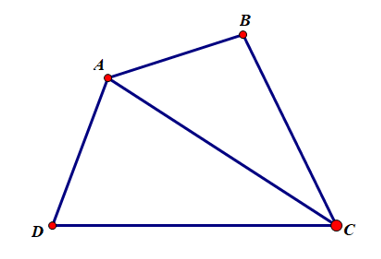
Bài 3. Chứng minh rằng trong tứ giác, mỗi đường chéo nhỏ hơn nửa chu vi tứ giác.

Hướng dẫn giải

Xét tứ giác ABCD có đường chéo AC:

AC < AB + BC (bất đẳng thức trong tam giác ABC)

AC < AD + DC (bất đẳng thức trong tam giác ADC)

Suy ra 2AC < AB + BC + AD + DC.

Do đó $AC<\frac{AB+BC+AD+DC\text{}}{2}$

Chứng minh tương tự, $BD<\frac{AB+BC+AD+DC\text{}}{2}$ .

Vậy trong tứ giác, mỗi đường chéo nhỏ hơn nửa chu vi tứ giác.