Lý thuyết Toán 8 Cánh diều Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 8 Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0) sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết Toán 8 Cánh diều Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)

A. Lý thuyết

1. Đồ thị của hàm số bậc nhất

Định nghĩa:

Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng.

Chú ý:

- Đồ thị của hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b (a ≠ 0).

- Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b.

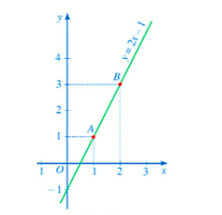
Ví dụ: Đồ thị dưới đây là đồ thị của hàm số bậc nhất y = 2x −1.

2. Cách vẽ đồ thị của hàm số bậc nhất

2.1. Cách vẽ đồ thị hàm số y = ax (a ≠ 0)

Cách vẽ:

Để vẽ đồ thị của hàm số y = ax (a ≠ 0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.

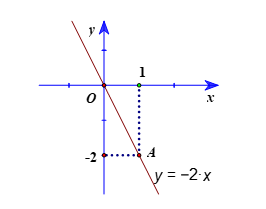
Ví dụ: Vẽ đồ thị của hàm số y = −2x.

Hướng dẫn giải

Với x = 1 thì y = −2, ta được A(1; −2) thuộc đồ thị hàm số y = −2x.

Vậy đồ thị của hàm số y = −2x là đường thẳng đi qua hai điểm O(0; 0) và A(1; −2).

2.2. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0; b ≠ 0)

Cách vẽ:

Để vẽ đồ thị của hàm số y = ax + b (a ≠ 0; b≠ 0), ta có thể xác định hai điểm P(0; b) và Q $\left(\frac{-b}{a};0\right)$ rồi vẽ đường thẳng đi qua hai điểm đó.

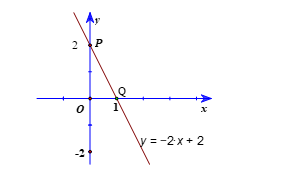
Ví dụ: Vẽ đồ thị của hàm số y = −2x + 2.

Hướng dẫn giải

Với x = 0 thì y = 2, ta được điểm P(0; 2) thuộc đồ thị của hàm số y = −2x + 2.

Với y = 0 thì x = 1, ta được điểm Q(1; 0) thuộc đồ thị của hàm số y = −2x + 2.

Vẽ đồ thị của hàm số y = −2x + 2 là đường thẳng đi qua hai điểm P(0; 2), Q(1; 0).

3. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

3.1. Góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox

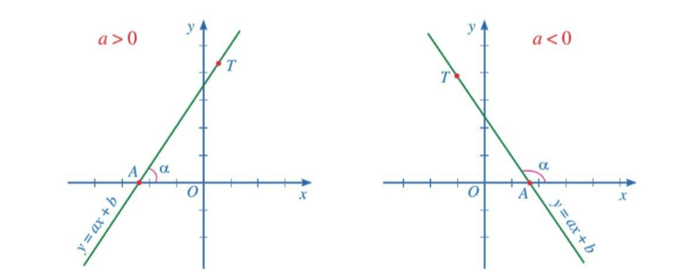
Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox. T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.

Góc α tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc α).

3.2. Hệ số góc

Định nghĩa:

Trên mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠ 0). Hệ số a gọi là hệ số góc của đường thẳng y = ax + b (a ≠ 0).

Chú ý:

- Khi hệ số a > 0 thì góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc càng lớn.

- Khi hệ số a < 0 thì góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn.

Ví dụ:

Hệ số góc của đường thẳng y = 2x + 1 là 2.

Hệ số góc của đường thẳng y = −x + 3 là −1.

3.3. Ứng dụng của hệ số góc

Cách nhận biết vị trí tương đối của hai đường thẳng trong mặt phẳng tọa độ Oxy:

Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0).

a) Nếu d song song với d’ thì a = a’; b ≠ b’. Ngược lại, nếu a = a’; b ≠ b’ thì d song song với d’.

b) Nếu d trùng với d’ thì a = a’; b = b’. Ngược lại, nếu a = a’; b = b’ thì d trùng với d’.

c) Nếu d và d’ cắt nhau thì a ≠ a’. Ngược lại, nếu a ≠ a’ thì d và d’ cắt nhau.

Ví dụ:

- Hai đường thẳng y = 2x + 1; y = 2x + 3 có hệ số góc bằng nhau và hệ số tự do khác nhau nên hai đường thẳng này song song.

- Hai đường thẳng y = 2x + 1; y = 3x có hệ số góc khác nhau nên hai đường thẳng này cắt nhau.

- Hai đường thẳng y = 3x – 1; y = 3x −1 có hệ số góc và hệ số tự do giống nhau nên hai đường thẳng này trùng nhau.

B. Bài tập vận dụng

Bài 1: Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong các đường thẳng sau: y = 3x + 1; y = 3x; y = −2x – 2.

Hướng dẫn giải

Cặp đường thẳng song song là: y = 3x + 1; y = 3x.

Cặp đường thẳng cắt nhau là: y = 3x + 1 và y = −2x – 2; y = 3x và y = −2x – 2.

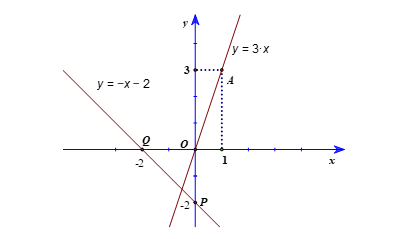
Bài 2: Vẽ đồ thị của các hàm số y = 3x; y = −x − 2 trên cùng một mặt phẳng tọa độ?

Hướng dẫn giải

+ Với x = 1 thì y = 3, ta được điểm A(1; 3) thuộc đồ thị hàm số y = 3x.

Vẽ đồ thị hàm số y = 3x là đường thẳng đi qua gốc tọa độ và điểm A.

+ Với x = 0 thì y = −2, ta được điểm P(0; −2) thuộc đồ thị hàm số y = −x − 2.

Với y = 0 thì x = −2, ta được điểm Q(−2; 0) thuộc đồ thị hàm số y = −x − 2.

Vẽ đồ thị hàm số y = −x – 2 là đường thẳng đi qua hai điểm P và Q.

Bài 3: a) Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 và đi qua điểm M(1; 2)?

b) Xác định đường thẳng y = ax + b (a ≠ 0) đi qua điểm M(1; 3) và song song với đường thẳng y = 2x?

Hướng dẫn giải

a) Vì đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 nên đường thẳng có dạng y = - x + b

y = −x + b.

Vì đường thẳng y = −x + b đi qua điểm M(1; 2) nên ta có: 2 = −1 + b $\Rightarrow$ b = 3.

Vậy y = −x + 3.

b) Vì đường thẳng y = ax + b (a ≠ 0) song song với đường thẳng y = 2x nên đường thẳng có dạng: y = 2x + b.

Mà đường thẳng y = 2x + b đi qua điểm M(1; 3) nên 3 = 2.1 + b $\Rightarrow$ b = 1.

Vậy y = 2x +1.