Lý thuyết tổng hợp Toán 8 Cánh diều Chương 3

---

Tổng hợp lý thuyết Toán 8 Chương 3 Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết tổng hợp Toán 8 Cánh diều Chương 3

A. Lý thuyết

1. Định nghĩa hàm số

Nếu đại lượng y phụ thuộc vào đại lượng x (x thay đổi) sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.

Chú ý:

+ Khi x thay đổi mà y luôn nhận một giá trị thì y được gọi là hàm hằng.

+ Hàm số có thể cho bằng công thức, bằng bảng.

+ Khi y là hàm số của x, ta có thể viết y = f(x), y = g(x),…

2. Giá trị của hàm số

Cho hàm số y = f(x) xác định tại x = a. Giá trị tương ứng của hàm số f(x) khi x = a được gọi là giá trị của hàm số y = f(x) tại x = a, kí hiệu là f(a).

3. Mặt phẳng tọa độ

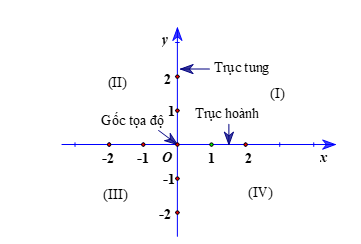
Trên mặt phẳng, ta vẽ hai trục số Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục. Khi đó ta có hệ trục tọa độ Oxy.

Trục Ox, Oy gọi là các trục tọa độ, Ox gọi là trục hoành, Oy gọi là trục tung. O gọi là gốc tọa độ.

Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.

Chú ý:

- Hai trục tọa độ chia mặt phẳng thành bốn góc: góc phần tư thứ I, góc phần tư thứ II, góc phần tư thứ III, góc phần tư thứ IV theo thứ tự ngược chiều quay của kim đồng hồ.

- Các đơn vị độ dài trên hai trục tọa độ được chọn bằng nhau (nếu không có lưu ý gì thêm).

4. Tọa độ của một điểm trong mặt phẳng tọa độ

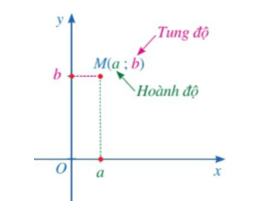
Cho điểm M trong mặt phẳng tọa độ Oxy. Giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy.

Cặp số (a; b) gọi là tọa độ của điểm M, a là hoành độ và b là tung độ của điểm M.

Điểm M có tọa độ (a; b) được kí hiệu là M(a; b).

Chú ý:

- Trong mặt phẳng tọa độ Oxy, mỗi điểm M xác định một cặp số (a; b). Ngược lại, mỗi cặp số (a; b) xác định một điểm M.

- Điểm nằm trên trục hoành có tung độ bằng 0.

- Điểm nằm trên trục tung có hoành độ bằng 0.

5. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ.

6. Định nghĩa hàm số bậc nhất y = ax + b (a ≠ 0)

Hàm số bậc nhất là hàm số được cho bởi công thức y = ax +b, trong đó a, b là các số cho trước và a khác 0.

Chú ý: Khi b = 0, ta có hàm số y = ax.

7. Đồ thị của hàm số bậc nhất

Định nghĩa: Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng.

Chú ý:

- Đồ thị của hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b (a ≠ 0).

- Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng cắt trục tung tại điểm có tung

8. Cách vẽ đồ thị của hàm số bậc nhất

8.1. Cách vẽ đồ thị hàm số y = ax (a ≠ 0)

Cách vẽ:

Để vẽ đồ thị của hàm số y = ax (a ≠ 0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.

8.2. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0; b ≠ 0)

Cách vẽ:

Để vẽ đồ thị của hàm số y = ax + b (a ≠ 0; b≠ 0), ta có thể xác định hai điểm P(0; b) và Q $\left(\frac{-b}{a};0\right)$ rồi vẽ đường thẳng đi qua hai điểm đó.

9. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

9.1. Góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox

Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox. T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.

Góc α tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc α).

9.2. Hệ số góc

Định nghĩa: Trên mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠ 0). Hệ số a gọi là hệ số góc của đường thẳng y = ax + b (a ≠ 0).

Chú ý:

- Khi hệ số a > 0 thì góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc càng lớn.

- Khi hệ số a < 0 thì góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn.

9.3. Ứng dụng của hệ số góc

Cách nhận biết vị trí tương đối của hai đường thẳng trong mặt phẳng tọa độ Oxy:

Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0).

a) Nếu d song song với d’ thì a = a’; b ≠ b’. Ngược lại, nếu a = a’; b ≠ b’ thì d song song với d’.

b) Nếu d trùng với d’ thì a = a’; b = b’. Ngược lại, nếu a = a’; b = b’ thì d trùng với d’.

c) Nếu d và d’ cắt nhau thì a ≠ a’. Ngược lại, nếu a ≠ a’ thì d và d’ cắt nhau.

B. Bài tập tự luyện

Bài 1. Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau:

Đại lượng y có phải là hàm số của đại lượng x không?

Hướng dẫn giải

Đại lượng y là hàm số của đại lượng x vì mỗi giá trị của x chỉ xác định đúng một giá trị của y.

Bài 2. Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau:

Đại lượng y có phải là hàm số của đại lượng x không?

Hướng dẫn giải

Đại lượng y không là hàm số của đại lượng x vì với giá trị x = 3 thì y nhận hai giá trị là 2 và 5.

Bài 3. Cho hàm số y = f(x) = 3x. Tính f(1); f(−2); $f\left(\frac{1}{3}\right)$ .

Hướng dẫn giải

f(1) = 3.1 = 3; f(−2) = 3.(−2) = −6 ; $f\left(\frac{1}{3}\right)=3.\frac{1}{3}=1$ .

Bài 4. Thời gian t (giờ) của một vật chuyển động đều trên quãng đường 20 km tỉ lệ nghịch với tốc độ v (km/h) của nó theo công thức $t=\frac{20}{v}$ . Đại lượng t có phải là hàm số của đại lượng v hay không? Nếu có, tính thời gian chuyển động của vật đó biết tốc độ của vật là 40 km/h?

Hướng dẫn giải

Đại lượng t là hàm số của đại lượng v vì mỗi giá trị của v ta nhận được chỉ một giá trị của t.

Với v = 40 km/h thì $t=\frac{20}{40}=\frac{1}{2}$  (giờ).

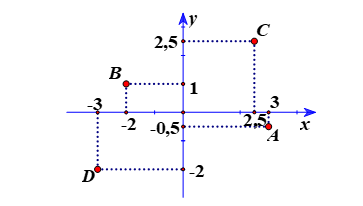
Bài 5. Vẽ mặt phẳng tọa độ Oxy và đánh dấu vị trí các điểm sau trên đó A(3; −0,5), B(−2; 1), C(2,5; 2,5), D(−3; −2).

Hướng dẫn giải

Cách xác định:

- Từ điểm biểu diễn hoành độ của điểm cho trước, kẻ một đường thẳng song song với trục tung.

- Tử điểm biểu diễn tung độ của điểm cho trước, kẻ một đường thẳng song song với trục hoành.

- Giao điểm của hai đường thẳng vừa dựng là điểm phải tìm.

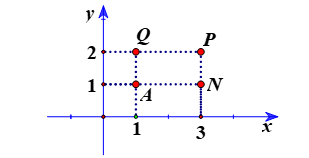
Bài 6. Viết tọa độ các điểm A, N, P, Q trong hình bên dưới.

Hướng dẫn giải

Cách xác định:

- Từ điểm đã cho kẻ đường thẳng song song với trục tung, cắt trục hoành tại một điểm biểu diễn hoành độ của điểm đó.

- Từ điểm đã cho kẻ đường thẳng song song với trục hoành, cắt trục tung tại một điểm biểu diễn tung độ của điểm đó.

- Hoành độ và tung độ tìm được là tọa độ của điểm đã cho.

Từ đó, ta các định được tọa độ các điểm là: A(1; 1), N(3; 1), P(3; 2), Q(1; 2).

Bài 7. Xác định các hệ số của x, hệ số tự do trong mỗi hàm số bậc nhất sau:

a) y = 3x – 4;

b) y = −x + 2;

c) $y=\frac{x}{2}$

Hướng dẫn giải

a) Hệ số của x là 3; hệ số tự do là −4.

b) Hệ số của x là −1; hệ số tự do là 2.

c) Hệ số của x là $\frac{1}{2}$ ; hệ số tự do là 0.

Bài 8. Cho hàm số bậc nhất f(x) = x −1. Tính f (1); f(0); f(−2).

Hướng dẫn giải

f(1) = 1 −1 = 0; f(0) = 0 −1 = −1; f(−2) = −2 −1 = −3.

Vậy f(1) = 0; f(0) = −1; f(−2) = −3.

Bài 9. Giá cước điện thoại cố định của một hãng viễn thông bao gồm cước thuê bao là 22000 đồng/tháng và cước gọi là 800 đồng/phút.

a) Lập công thức tính số tiền cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút?

b) Tính số tiền cước điện thoại phải trả khi gọi 75 phút?

c) Nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi bao nhiêu phút?

Hướng dẫn giải

a) Công thức tính số tiền cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút là: y = 800x + 22 000.

b) Số tiền cước điện thoại phải trả khi gọi 75 phút là:

y = 800 . 75 + 22 000 = 82 000 (đồng).

Vậy số tiền cước điện thoại phải trả khi gọi 75 phút là 82 000 đồng.

c) Số tiền cước điện thoại phải trả là 94000 đồng thì trong tháng đó thuê bao đã gọi số phút là:

94 000 = 800.x + 22 000

800x = 94 000 − 22 000 

800x = 72 000 

Do đó x = 90.

Vậy nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi 90 phút.

Bài 10. Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong các đường thẳng sau: y = 3x + 1; y = 3x; y = −2x – 2.

Hướng dẫn giải

Cặp đường thẳng song song là: y = 3x + 1; y = 3x.

Cặp đường thẳng cắt nhau là: y = 3x + 1 và y = −2x – 2; y = 3x và y = −2x – 2.

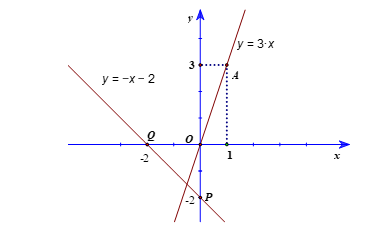
Bài 11. Vẽ đồ thị của các hàm số y = 3x; y = − x − 2 trên cùng một mặt phẳng tọa độ?

Hướng dẫn giải

+ Với x = 1 thì y = 3, ta được điểm A(1; 3) thuộc đồ thị hàm số y = 3x.

Vẽ đồ thị hàm số y = 3x là đường thẳng đi qua gốc tọa độ và điểm A.

+ Với x = 0 thì y = −2, ta được điểm P(0; −2) thuộc đồ thị hàm số y = − x − 2.

Với y = 0 thì x = −2, ta được điểm Q(−2; 0) thuộc đồ thị hàm số y = − x − 2.

Vẽ đồ thị hàm số y = − x – 2 là đường thẳng đi qua hai điểm P và Q.

Bài 12.

a) Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 và đi qua điểm M(1; 2)?

b) Xác định đường thẳng y = ax + b (a ≠ 0) đi qua điểm M(1; 3) và song song với đường thẳng y = 2x?

Hướng dẫn giải

a) Vì đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 nên đường thẳng có dạng

y = −x + b.

Vì đường thẳng y = −x + b đi qua điểm M(1; 2) nên ta có: 2 = −1 + b hay b = 3.

Vậy y = −x + 3.

b) Vì đường thẳng y = ax + b (a ≠ 0) song song với đường thẳng y = 2x nên đường thẳng có dạng: y = 2x + b.

Mà đường thẳng y = 2x + b đi qua điểm M(1; 3) nên 3 = 2.1 + b hay b = 1.

Vậy y = 2x +1.