Lý thuyết Toán 8 Cánh diều Bài 7: Hình vuông
Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 8 Bài 7: Hình vuông sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.
Lý thuyết Toán 8 Cánh diều Bài 7: Hình vuông
A. Lý thuyết
1. Định nghĩa
Ta có định nghĩa:
Hình vuông là hình tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
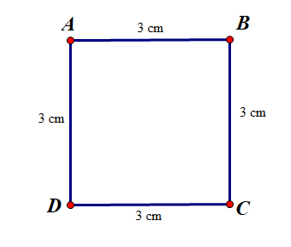
Ví dụ: Chứng minh tứ giác ABCD là hình vuông.
Hướng dẫn giải
Ta có và AB = BC = CD = DA (vì cùng bằng 3 cm).
Suy ra tứ giác ABCD là hình vuông.
2. Tính chất
Ta có định lý sau:
Trong một hình vuông:
- Các cạnh đối song song;
- Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;
- Hai đường chéo là các đường phân giác của các góc ở đỉnh.
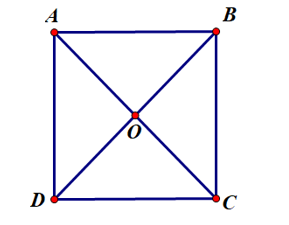
Ví dụ: Cho hình vuông ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh các tam giác OAB, OBC, OCD, ODA là những tam giác vuông cân.
Hướng dẫn giải
Do ABCD là hình vuông cân nên AC = BD, , AC và BD cắt nhau tại trung điểm O của mỗi đường.
Suy ra các tam giác OAB, OBC, OCD, ODA là những tam giác vuông cân tại O và OA= OB = OC = OD.
Vậy các tam giác OAB, OBC, OCD, ODA là những tam giác vuông cân.
3. Dấu hiệu nhận biết
Ta có những dấu hiệu nhận biết:
- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông;
- Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông;
- Hình chữ nhật có một đường chéo là đường phân giác cảu một góc là hình vuông.
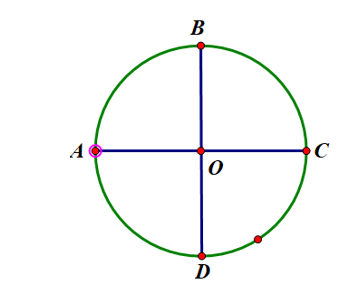
Ví dụ: Cho đường tròn tâm O. Giả sử AC và BD là hai đường kính của đường trong sao cho . Chứng minh ABCD là hình vuông.
Hướng dẫn giải
Vì tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường nên ABCD là hình bình hành.
Hình bình hành ABCD có AC = BD nên ABCD là hình chữ nhật.
Hình chữ nhật ABCD có hai đừng chéo vuông góc với nhau nên ABCD là hình vuông.
Vậy ABCD là hình vuông.
B. Bài tập tự luyện
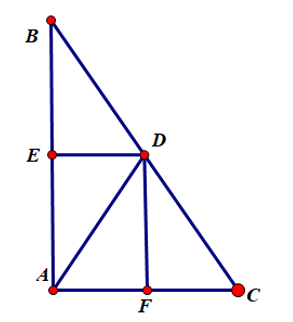
Bài 1. Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.
Hướng dẫn giải
Xét tứ giác AEDF có:
Suy ra AEDF là hình chữ nhật (1)
Theo giả thiết ta có: AD là đường phân giác của góc .
Suy ra .
Xét ΔAED có:
Suy ra .
Suy ra ΔAED vuông cân tại E nên AE = ED (2).
Từ (1) và (2) suy ra AEDF là hình vuông.
Vậy AEDF là hình vuông.
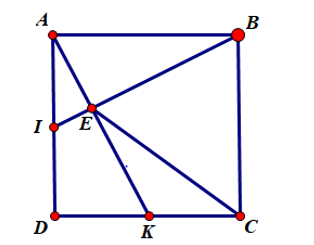
Bài 2. Cho hình vuông ABCD. Gọi I, K lần lượt là trung điểm của AD và DC.
a) Chứng minh rằng BI ⊥ AK.
b) Gọi E là giao điểm của BI và AK. Chứng minh rằng .
Hướng dẫn giải
Xét ∆BAI và ∆ADK có:
AB = AD
Suy ra ∆BAI = ∆ADK (c.g.c)
Suy ra (góc tương ứng bằng nhau)
Mà
Suy ra
• Xét ∆ABE có
Suy ra
Hay AK ⊥ BI (đpcm)
• Xét tứ giác EBCK có
Suy ra
Mà .
Do đó .