Lý thuyết Toán 8 Cánh diều Bài 3: Hình thang cân

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 8 Bài 3: Hình thang cân sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết Toán 8 Cánh diều Bài 3: Hình thang cân

A. Lý thuyết

1. Định nghĩa

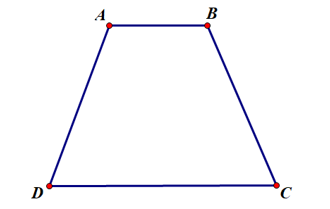
Hình thang là tứ giác có hai cạnh đối song song.

Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

Chú ý: Nếu ABCD là hình thang cân (AB // CD) thì $\widehat{A}=\widehat{B}$  và $\widehat{\text{C}}\text{ = }\widehat{\text{D}}$ .

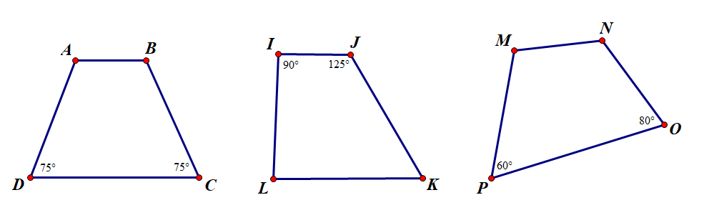
Ví dụ: Trong hình vẽ sau, hình nào là hình thang cân?

Hướng dẫn giải

Trong các hình trên, chỉ có ABCD là hình thang cân vì có $\widehat{\text{C}}$  và $\widehat{D}$  cùng kề đáy và $\widehat{\text{C}}\text{ = }\widehat{\text{D}}\text{ = 75}°$ .

2. Tính chất

Trong một hình thang cân:

- Hai cạnh bên bằng nhau;

- Hai đường chéo bằng nhau.

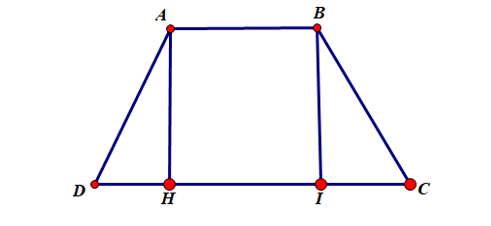
Ví dụ: Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi H, K lần lượt là hình chiếu của A, B trên đường thẳng CD. Chứng minh DH = CK.

Hướng dẫn giải

Xét hai tam giác vuông ADH và BCK, ta có:

AD = BC; $\widehat{ADH}=\widehat{BCK}$  (vì ABCD là hình thang cân).

Suy ra $\text{ΔADH = ΔBCK}$ (cạnh huyền – góc nhọn).

Do đó DH = CK (hai cạnh tương ứng).

3. Dấu hiệu nhận biết

Hình thang có hai đường chéo bằng nhau là hình thang cân.

Ví dụ: Cho tứ giác ABCD có AB < CD, hai đường chéo AC và  BD bằng nhau, $\widehat{\text{BAC}}\text{ = }\widehat{\text{ACD}}$ . Chứng minh tứ giác ABCD là hình thang cân.

Hướng dẫn giải

Do $\widehat{BAC}=\widehat{ACD}$  và $\widehat{\text{BAC}}$ , $\widehat{\text{ACD}}$  nằm ở vị trí so le trong nên AB // CD.

Suy ra tứ giác ABCD là hình thang.

Vì hình thang ABCD có AC = BD nên ABCD là hình thang cân.

B. Bài tập tự luyện

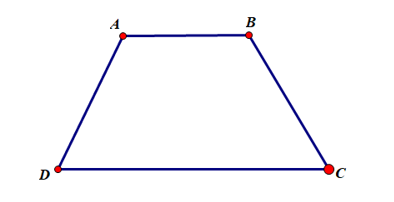
Bài 1. Cho hình thang cân ABCD (như hình vẽ) có $\widehat{\text{BAD}}=60°.$  Số đo của $\widehat{\text{BCD}}$  bằng bao nhiêu?

Hướng dẫn giải

Vì ABCD là hình thang cân nên ta có: $\widehat{\text{A}}\text{ = }\widehat{\text{B}}$  và $\widehat{\text{C}}\text{ = }\widehat{\text{D}}$ .

Mà $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$ . Suy ra $2\widehat{A}+2\widehat{C}=360°$ .

Nên $2\widehat{C}=360°-2\widehat{A}=360°-2.60°=240°.$  Suy ra $\widehat{C}=120°.$

Vậy $\widehat{C}=120°.$

Bài 2. Cho hình thang cân ABCD đáy nhỏ AB = 4 cm, đáy lớn CD = 10 cm, cạnh bên BC = 5 cm. Tính đường cao AH.

Hướng dẫn giải

Kẻ BI ⊥ CD tại I.

Vì ABCD là hình thang cân nên ta có:

 $\widehat{\text{D}}=\widehat{\text{C}}$

AD = BC

Do đó ΔAHD = ΔBKC (cạnh huyền – góc nhọn)

Suy ra DH = CK.

Hay $DH=\frac{1}{2}(CD-AB)=\frac{1}{2}(10-4)=3\text{ (}cm).$

Do ABCD là hình thang cân nên AD = BC = 5 cm.

Áp dụng định lý Pythagore vào tam giác ADH vuông tại H, ta có:

AD² = AH² + DH²

Suy ra AH² = AD² – DH² = 5² – 3² = 16.

Do đó AH = 4 cm.