Lý thuyết Toán 8 Cánh diều Bài 2: Hình chóp tứ giác đều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 8 Bài 2: Hình chóp tứ giác đều sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết Toán 8 Cánh diều Bài 2: Hình chóp tứ giác đều

A. Lý thuyết

1. Hình chóp tứ giác đều

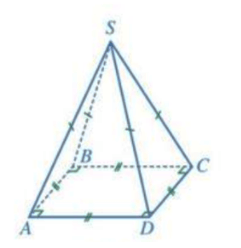
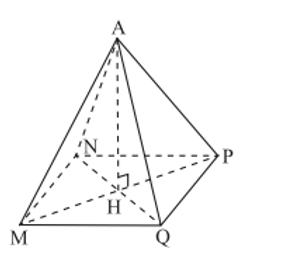
- Hình chóp tứ giác đều S.ABCD;

- Mặt đáy ABCD là một hình vuông;

- Các mặt bên SAB, SBC, SCD, SDA là những tam giác cân tại S;

- Các cạnh đáy AB, BC, CD, DA bằng nhau;

- Các cạnh bên SA, SB, SC, SD bằng nhau;

- Gọi S là đỉnh của hình chóp tứ giác đều S.ABCD.

Chú ý:

Hình chóp tứ giác đều có 5 mặt, 8 cạnh.

2. Diện tích xung quanh của hình chóp tứ giác đều

2.1. Trung đoạn của hình chóp tứ giác đều

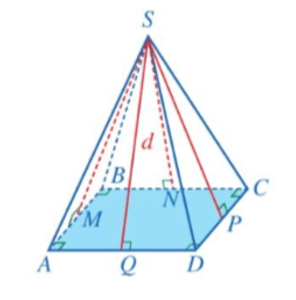
Cho hình chóp tứ giác đều S.ABCD. Gọi SM, SN, SP, SQ lần lượt là đường cao của các tam giác SAB, SBC, SCD, SDA. Mỗi đoạn thẳng SM, SN, SP, SQ đều được gọi là trung đoạn của hình chóp tứ giác đều S.ABCD.

2.2. Công thức tính diện tích xung quanh của hình chóp tứ giác đều

Cách tính:

Diện tích xung quanh của hình chóp tứ giác đều bằng nửa tích của chu vi đáy với độ dài trung đoạn.

Tức là:

$S_{xq}=\frac{1}{2}.C.d$, trong đó S_xq là diện tích xung quanh, C là chu vi đáy, d là độ dài trung đoạn của hình chóp tứ giác đều.

Ví dụ:

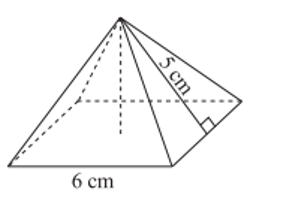
Tính diện tích xung quanh của hình chóp tứ giác đều biết độ dài cạnh đáy bằng 10 cm và độ dài trung đoạn bằng 7 cm?

Hướng dẫn giải

Chu vi đáy của hình chóp tứ giác đều là: 10 . 4 = 40 (cm).

Diện tích xung quanh của hình chóp tứ giác đều là $S_{xq}=\frac{1}{2}.40.7=140$  (cm²).

Vậy diện tích xung quanh của hình chóp tứ giác đều là 140 cm².

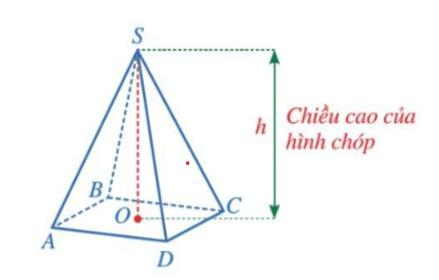
3. Thể tích của hình chóp tứ giác đều

Cách tính:

Thể tích của hình chóp tứ giác đều bằng một phần ba tích của diện tích đáy với chiều cao.

Tức là:

$V=\frac{1}{3}.S.h$, trong đó V là thể tích, S là diện tích đáy, h là chiều cao của hình chóp tứ giác đều.

Ví dụ:

Tính thể tích của hình chóp tứ giác đều với độ dài cạnh đáy là 8 cm và chiều cao là 9 cm?

Hướng dẫn giải

Diện tích đáy của hình chóp tứ giác đều là: 8.8 = 64 (cm²).

Thể tích hình chóp tứ giác đều là: $V=\frac{1}{3}\mathrm{.64.9}=192$  (cm³).

Vậy thể tích hình chóp tứ giác đều là 192 cm³.

B. Bài tập vận dụng

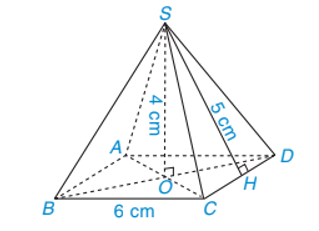
Bài 1: Một hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 6 cm, độ dài trung đoạn bằng 5 cm và chiều cao bằng 4 cm.

a) Tính diện tích xung quanh của hình chóp tứ giác đều đó?

b) Tính thể tích của hình chóp tứ giác đều đó?

Hướng dẫn giải

a) Chu vi đáy của hình chóp tứ giác đều là: 6 . 4 = 24 (cm).

Diện tích xung quanh của hình chóp tứ giác đều là: $S_{xq}=\frac{1}{2}.24.5=60$  (cm²).

Vậy diện tích xung quanh của hình chóp tứ giác đều là 60 cm².

b) Diện tích đáy của hình chóp tứ giác đều là: 6 . 6 = 36 (cm²).

Thể tích của hình chóp tứ giác đều là: $V=\frac{1}{3}.36.4=48$  (cm³).

Thể tích của hình chóp tứ giác đều là 48 cm³.

Bài 2: Tính chiều cao AH của hình chóp tứ giác đều A.MNPQ biết độ dài cạnh đáy hình vuông MNPQ là 8cm và thể tích của hình chóp tứ giác đều đó là 192 cm³?

Hướng dẫn giải

Diện tích đáy MNPQ là: S = 8.8 = 64 (cm²).

Độ dài chiều cao AH là: $\frac{3.V_{A.MNPQ}}{S}=\frac{3.192}{64}=9$  (cm).

Vậy độ dài chiều cao AH là 9 cm.

Bài 3: Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp tứ giác đều với độ dài cạnh đáy của hình chóp là 6 m, trung đoạn của hình chóp là 5 m. Bác Khôi muốn sơn bốn mặt xung quanh của hộp gỗ. Cứ mỗi mét vuông sơn cần trả 30 000 đồng (tiền sơn và tiền công). Hỏi bác Khôi phải trả chi phí là bao nhiêu?

Hướng dẫn giải

Chu vi đáy của chiếc hộp là: 6.4 = 24 (m).

Diện tích xung quanh của chiếc hộp là: $S_{xq}=\frac{1}{2}\mathrm{.24.5}=60$  (m²).

Diện tích sơn chính là diện tích xung quanh của chiếc hộp.

Do đó số tiền bác Khôi phải trả là: 60. 30 000 = 1 800 000 (đồng).

Vậy số tiền bác Khôi phải trả là 1 800 000 đồng.