Lý thuyết Toán 8 Cánh diều Bài 5: Hình chữ nhật

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 8 Bài 5: Hình chữ nhật sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết Toán 8 Cánh diều Bài 5: Hình chữ nhật

A. Lý thuyết

1. Định nghĩa

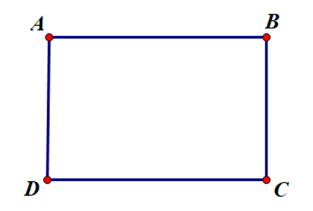
Hình chữ nhật là tứ giác có bốn góc vuông.

Ví dụ: Cho tứ giác ABCD có $\widehat{A}=\widehat{B}=\widehat{C}=90°$ . Chứng minh ABCD là hình chữ nhật.

Hướng dẫn gải

Tứ giác ABCD có: $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$

Suy ra $\widehat{D}=360°-\widehat{A}-\widehat{B}-\widehat{C}=90°$

Do đó $\widehat{A}=\widehat{B}=\widehat{C}=90°$ .

Vậy tứ giác ABCD là hình chữ nhật.

2. Tính chất

Trong một hình chữ nhật:

- Hai cạnh đối song song và bằng nhau;

- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

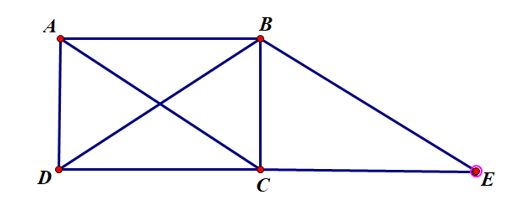
Ví dụ: Cho hình chữ nhật ABCD và hình bình hành ABEC.

Chứng minh BD = BE.

Hướng dẫn giải

Ta có: ABCD là hình chữ nhật nên AC = BD;

ABEC là hình bình hành nên BE = AC.

Suy ra BD = BE (vì cùng bằng AC).

Vậy BD = BE.

3. Dấu hiệu nhận biết

Ta có những dấu hiệu nhận biết:

- Hình bình hành có một góc vuông là hình chữ nhật.

- Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

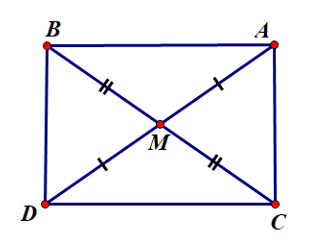
Ví dụ: Cho tam giác ABC có đường trung tuyến $AM=\frac{1}{2}BC$ . Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh:

a) Tứ giác ABDC là hình chữ nhật

b) Tam giác ABC vuộng tại A.

Hướng dẫn giải

a) Vì tứ giác ABDC có hai đường chéo AD, BC cắt nhau tại trung điểm M của mỗi đường nên ABDC là hình bình hành.

Do $AM=\frac{1}{2}BC$  và $AM=\frac{1}{2}AD$  (vì M là trung điểm của AD) nên BC = AD.

Hình bình hành ABDC có hai đường chéo BC, AD bằng nhau nên ABDC là hình chữ nhật.

Vậy ABDC là hình chữ nhật.

b) Do ABDC là hình chữ nhật nên $\widehat{BAC}=90°$ .

Do đó tam giác ABC vuông tại A.

B. Bài tập tự luyện

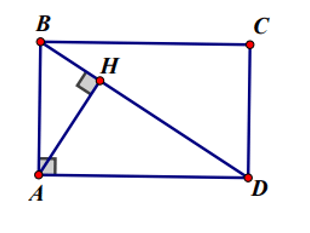
Bài 1. Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HB = 2 cm, HD = 6 cm. Tính độ dài AB, AD.

Hướng dẫn giải

Ta có: BD = HB + HD = 2 + 6 = 8 (cm).

Xét tam giác giác BHA vuông tại H ta có:  BH² + AH² = AB²

Suy ra AH² = AB² – BH²

Suy ra AH² = AB² – 4      (1)

Xét tam giác AHD vuông tại H ta có: HD² + AH² = AD²

Suy ra AH² = AD² – HD²

Suy ra AH² = AD² – 3     (2)

Từ (1) và (2) suy ra AB² – 4 = AD² – 36       (3)

Xét tam giác ABD vuông tại A có:

AB² + AD² = DB²  = 8² = 64

Thay AB² = 64 – AD²  vào (3). Giải ra ta được AD² = 48 hay $AD=4\sqrt{3}$ .

Suy ra AB = 4 cm.

Vậy $AD=4\sqrt{3}$  cm và AB = 4 cm.

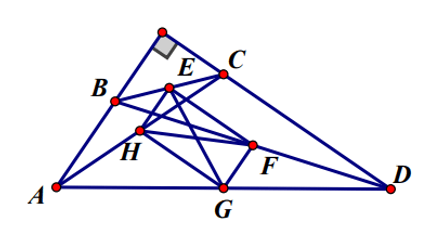
Bài 2. Tứ giác ABCD có AB ⊥ CD. Gọi E, F, G, H theo thứ tự là trung điểm của BC, BD, AD, AC. Chứng minh rằng EG = FH.

Hướng dẫn giải

Vì E là trung điểm của BC; H là trung điểm của AC .

Nên EH là đường trung bình của ΔBCD

Suy ra EF // CI

Kết hợp với AB ⊥ CD  (gt)      (4)

Kết hợp (*), (3) và (4)

Suy ra HE⊥ EF

Suy ra HEF = 90° (***)

Từ (**) và (***) ta có EFGH là hình chữ nhật.

Từ đó hai đường chéo EG = FH.

Vậy EG = FH.

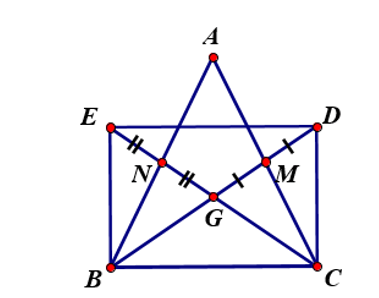
Bài 3. Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?

Hướng dẫn giải

Ta có hai đường trung tuyến BM và CN cắt nhau tại G nên G là trọng tâm tam giác ABC.

Theo tính chất trọng tâm tam giác ta có: BG = 2GM

CG = 2GN 

Lại có: G đối xứng với với D qua M suy ra GM = MD hay GD = 2GM

G đối xứng với E qua N suy ra GN = EN hay GE = 2GN

Do đó BG = GD và CG = GE

Suy ra G là trung điểm của BD và CE.

Xét tứ giác BCDE có: G là trung điểm của đường chéo BD

G là trung điểm đường chéo CE

Suy ra tứ giác BCDE là hình bình hành.

Lại có: $∆$ABC cân tại A nên AB = AC.

Mà M là trung điểm của AC, N là trung điểm AB nên BN = CM.

Xét $∆$BNC và $∆$CMB có:

Cạnh BC chung

BN = CM

 $\widehat{NBC}=\widehat{MCB}$(do tam giác ABC cân tại A)

Do đó $∆$BNC = $∆$CMB (c.g.c)

Suy ra CN = BM (hai cạnh tương ứng)

Mà $CN=\frac{3}{4}EC$  và $\text{BM}=\frac{3}{4}BD$

Do đó EC = BD.

Xét hình bình hành BCDE có hai đường chéo EC và BD bằng nhau.

Vậy tứ giác BCDE là hình chữ nhật.