Bài 4 trang 23 Chuyên đề Toán 11 Cánh diều

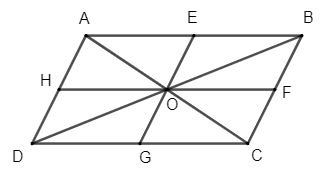
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Xét phép đối xứng tâm O, xác định ảnh của:

Giải Chuyên đề Toán 11 Bài 1: Phép dời hình - Cánh diều

Bài 4 trang 23 Chuyên đề Toán 11: Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Xét phép đối xứng tâm O, xác định ảnh của:

a) Trung điểm các cạnh AB, BC, CD, DA;

b) Các đường thẳng AB, AC.

Lời giải:

Bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều

a) Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

Vì O là giao hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.

Xét tam giác ABC có E và O lần lượt là trung điểm của AB và AC nên OE là đường trung bình của tam giác ABC, suy ra OE // BC và OE = $\frac{1}{2}$ BC (1).

Xét tam giác DBC có O và G lần lượt là trung điểm của DB và DC nên OG là đường trung bình của tam giác DBC, suy ra OG // BC và OG = $\frac{1}{2}$ BC (2).

Từ (1) và (2) suy ra E, O, G thẳng hàng và OE = OG. Do đó, O là trung điểm của EG.

Chứng minh tương tự ta được O là trung điểm của HF.

Như vậy, ảnh của các điểm E, F, G, H qua phép đối xứng tâm O lần lượt là các điểm G, H, E, F.

b) Vì O là trung điểm của AC và BD nên ta có phép đối xứng tâm O biến các điểm A, B, C thành các điểm C, D, A.

Do đó, phép đối xứng tâm O biến đường thẳng AB thành đường thẳng CD, biến đường thẳng AC thành đường thẳng CA (chính nó).

Lời giải Chuyên đề Toán 11 Bài 1: Phép dời hình hay, chi tiết khác:

Xem thêm lời giải bài tập Chuyên đề học tập Toán 11 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯