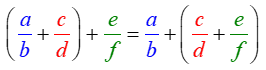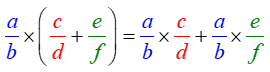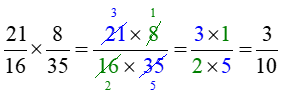Lý thuyết Toán lớp 5 Chân trời sáng tạo Học kì 1 (hay nhất)

---

Haylamdo biên soạn tóm tắt Lý thuyết Toán lớp 5 Học kì 1 Chân trời sáng tạo gồm đầy đủ lý thuyết, bài tập minh họa có lời giải sẽ giúp học sinh lớp 5 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 5.

Lý thuyết Toán lớp 5 Chân trời sáng tạo Học kì 1 (hay nhất)

Lý thuyết Toán lớp 5 Chân trời sáng tạo Học kì 1

Lý thuyết Chương 1: Ôn tập và bổ sung

Lý thuyết Chương 2: Số thập phân

Lý thuyết Chương 3: Hình tam giác, hình thang, hình tròn

Lý thuyết Ôn tập và bổ sung các phép tính với phân số

I. Lý thuyết

1. Ôn tập các phép tính với phân số (các kiến thức đã học của lớp 4).

1.1. Quy đồng mẫu số các phân số (Một mẫu chia hết cho mẫu còn lại)

Ví dụ: Quy đồng mẫu số hai phân số $\frac{3}{2}$ và $\frac{5}{16}$.

• Chọn mẫu số chung:

Vì 16 chia hết cho 2 (16 : 2 = 8) nên ta chọn mẫu số chung là: 16

Thực hiện quy đồng mẫu số:

$\frac{3}{2}=\frac{3\times 8}{2\times 8}=\frac{24}{16}$ và giữ nguyên phân số $\frac{5}{16}$

Vậy quy đồng mẫu số hai phân số $\frac{3}{2}$ và $\frac{5}{16}$ ta được hai phân số $\frac{24}{16}$ và $\frac{5}{16}$.

1.2. Phép cộng phân số

a) Cộng hai phân số cùng mẫu.

Ví dụ: $\frac{5}{9}+\frac{2}{9}=\frac{5+2}{9}=\frac{7}{9}$

b) Cộng hai phân số khác mẫu.

Ví dụ: $\frac{3}{5}+\frac{9}{20}=\frac{12}{20}+\frac{9}{20}=\frac{12+9}{20}=\frac{21}{20}$

c) Các tính chất của phép cộng phân số:

• Phép cộng phân số có tính chất giao hoán

• Phép cộng phân số có tính chất kết hợp

• Một phân số cộng với 0 bằng chính phân số đó.

$\frac{a}{b}+0=0+\frac{a}{b}=\frac{a}{b}$

Ví dụ:

$\frac{3}{7}+\frac{2}{5}+\frac{4}{7}$ = $\frac{3}{7}+\frac{4}{7}+\frac{2}{5}$ = $\left(\frac{3}{7}+\frac{4}{7}\right)+\frac{2}{5}$ = $1+\frac{2}{5}=\frac{7}{5}$

$\frac{2}{3}+0=\frac{2}{3}$

1.2. Phép trừ phân số

a) Trừ hai phân số cùng mẫu.

Ví dụ:

$\frac{5}{7}-\frac{3}{7}=\frac{5-3}{7}=\frac{2}{7}$

b) Trừ hai phân số khác mẫu.

Ví dụ:

$\frac{3}{4}-\frac{5}{8}=\frac{6}{8}-\frac{5}{8}=\frac{6-5}{8}=\frac{1}{8}$

1.3. Phép nhân phân số

Ví dụ:

$\frac{2}{3}\times \frac{5}{7}=\frac{2\times 5}{3\times 7}=\frac{10}{21}$

Nhận xét:

• Phép nhân các phân số có tính chất giao hoán.

• Phép nhân các phân số có tính chất kết hợp.

• Một phân số nhân với 1 bằng chính phân số đó.

$\frac{a}{b}\times 1=1\times \frac{a}{b}=\frac{a}{b}$

• Tính chất nhân một số với một tổng được áp dụng với các phân số.

1.3. Phép chia phân số

a) Phân số đảo ngược:

Ví dụ: Phân số đảo ngược của phân số $\frac{5}{6}$ là phân số $\frac{6}{5}$

b) Phép chia phân số

Ví dụ:

$\frac{2}{3}:\frac{5}{7}=\frac{2}{3}\times \text{\hspace{0.17em}}\frac{7}{5}=\frac{14}{15}$

2. Bổ sung các phép tính với phân số.

2.1. Quy đồng mẫu số các phân số (Trường hợp không có mẫu số chung)

Ví dụ: Quy đồng mẫu số các phân số $\frac{2}{3}$ và $\frac{4}{5}$

Vì 3 × 5 = 15 nên ta chọn 15 làm mẫu số chung.

$\frac{2}{3}=\frac{2\times 5}{3\times 5}=\frac{10}{15}$

$\frac{4}{5}=\frac{4\times 3}{5\times 3}=\frac{12}{15}$

Vậy quy đồng mẫu số hai phân số $\frac{2}{3}$ và $\frac{4}{5}$ ta được hai phân số $\frac{10}{15}$ và $\frac{12}{15}$

Lưu ý: Khi quy đồng mẫu số hai phân số khác mẫu số, ta nên chọn số bé nhất (lớn hơn 0) chia hết cho cả hai mẫu số làm mẫu số chung.

Ví dụ: Quy đồng mẫu số hai phân số $\frac{5}{8}$ và $\frac{7}{12}$

Vì 24 là số bé nhất lớn hơn 0 chia hết cho 8 và 12 nên ta chọn 24 làm mẫu số chung.

Ta có:

$\frac{5}{8}=\frac{5\times 3}{8\times 3}=\frac{15}{24}$

$\frac{7}{12}=\frac{7\times 2}{12\times 2}=\frac{14}{24}$

Vậy quy đồng mẫu số hai phân số $\frac{5}{8}$ và $\frac{7}{12}$ ta được hai phân số $\frac{15}{24}$ và $\frac{14}{24}$

2.2. Phép cộng phân số

Ví dụ:

$\frac{3}{5}+\frac{2}{7}=\frac{21}{35}+\frac{10}{35}=\frac{31}{35}$

2.3. Phép trừ phân số

Ví dụ:

$\frac{3}{5}-\frac{2}{7}=\frac{21}{35}-\frac{10}{35}=\frac{11}{35}$

Chú ý: Khi thực hiện phép cộng, trừ hai phân số cần lưu ý

- Xác định xem các phân số cùng mẫu hay khác mẫu số.

- Nếu cùng mẫu số, cộng, trừ tử số với tử số, dưới gạch ngang chỉ viết một mẫu số chung.

- Nếu khác mẫu số ⟶ Quy đồng mẫu số ⟶ Cộng, trừ hai phân số cùng mẫu số.

- Kết quả cuối cùng là phân số tối giản.

2.4. Phép nhân phân số

Ví dụ:

................................

................................

................................

Lý thuyết Phân số thập phân

I. Lý thuyết

1. Khái niệm phân số thập phân.

Các phân số có mẫu số là 10; 100; 1000; .... được gọi là các phân số thập phân.

Ví dụ:

Các phân số ; ... là những phân số thập phân.

2. Chuyển đổi một số phân số không phải là phân số thập phân thành phân số thập phân

– Những phân số mà 10; 100; 1 000; … chia hết cho mẫu số thì có thể viết dưới dạng phân số thập phân.

– Những phân số mà 10; 100; 1 000; … không chia hết cho mẫu số thì không thể viết dưới dạng phân số thập phân.

– Cách viết phân số thành phân số thập phân:

+ Lấy 10; 100; 1000;… chia cho mẫu số.

+Được bao nhiêu ta nhân cả tử số và mẫu số với số đó. Ta được phân số mới là phân số thập phân.

Hoặc:

+ Lấy mẫu số chia cho 10; 100; 1000;…

+Được bao nhiêu ta lấy cả tử số và mẫu số chia cho số đó. Ta được phân số mới là phân số thập phân.

Ví dụ 1: Viết phân số $\frac{3}{5}$ thành phân số thập phân:

+ Lấy 10 : 5 = 2

+ Lấy $\frac{3}{5}=\frac{3\times 2}{5\times 2}$= . Vậy ta được phân số là phân số thập phân.

Ví dụ 2: Viết phân số $\frac{27}{20}$thành phân số thập phân:

+ Lấy 100 : 20 = 5

+ Lấy $\frac{27}{20}=\frac{27\times 5}{20\times 5}$= . Vậy ta được phân số là phân số thập phân.

Ví dụ 3: Viết phân số $\frac{5}{500}$ thành phân số thập phân:

+ Lấy 500 : 5 = 100

+ Lấy $\frac{5}{500}=\frac{5:5}{500:5}$= . Vậy ta được phân số là phân số thập phân.

................................

................................

................................