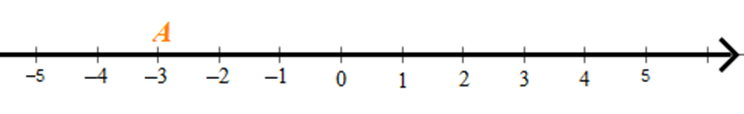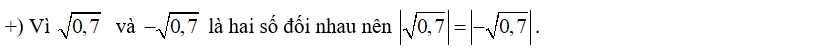15 Bài tập Giá trị tuyệt đối của một số thực (có đáp án) - Cánh diều Trắc nghiệm Toán 7
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Giá trị tuyệt đối của một số thực Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.
15 Bài tập Giá trị tuyệt đối của một số thực (có đáp án) - Cánh diều Trắc nghiệm Toán 7
Câu 1. Trên trục số, khoảng cách từ điểm – 3 đến điểm gốc 0 là:
A. – 3;
B. 3;
C. 1,5;
D. 6;
Hiển thị đáp án
Đáp án đúng là: B.
Điểm A biểu diễn số – 3 trên trục số như sau:
Khoảng cách từ điểm A đến gốc 0 là 3 đơn vị.
Câu 2. Chọn phát biểu đúng .
A. Giá trị tuyệt đối của một số luôn là một số dương;
B. Giá trị tuyệt đối của một số luôn là một số không âm;
C. Giá trị tuyệt đối của một số luôn là một số không dương.
D. Giá trị tuyệt đối của một số luôn là một số âm.
Hiển thị đáp án
Đáp án đúng là: B.
Giá trị tuyệt đối của một số luôn là một số không âm: |x| ≥ 0 với mọi số thực x.
Câu 3. Với mọi x ∈ ℚ sai ?
A. |x| = |–x|;
B. |x| < –x;
C. |x| ≥ 0;
D. |x| ≥ x.
Hiển thị đáp án
Đáp án đúng là: B.
Với mọi x ∈ ℚ | x| = |–x|; |x| ≥ 0 và |x| ≥ x nên B sai.
Với x ≥
Với x < 0 thì |x| = - x
Nên |x| ≥
Câu 4. Giá trị tuyệt đối của - 16 6
A. - 8 3 ;
B. 8 3
C. - 16 6
D. 6 16 ;
Hiển thị đáp án
Đáp án đúng là: B.
Vì - 16 6 < 0
Vậy giá trị tuyệt đối của - 16 6 8 3 ·
Câu 5. Chọn khẳng định sai :
Hiển thị đáp án
Đáp án đúng là: C.
Vì –2,5 < 0 nên |–2,5| = –(–2,5) = 2,5. Do đó phương án A đúng.
Vì |0| = 0 nên phương án B đúng.
Vì 3,8 > 0 nên |3,8| = 3,8. Do đó phương án C sai.
Do đó phương án D đúng.
Câu 6. Chọn khẳng định đúng .
Hiển thị đáp án
Đáp án đúng là: D.
+) Ta có –0,6 < 0 nên |–0,6| = –(–0,6) = 0,6. Do đó phương án B sai.
Vì –0,7 < 0 nên |–0,7| = –(–0,7) = 0,7.
Vì 0,6 < 0,7 nên |–0,6| < |–0,7|. Do đó phương án A sai.
Do đó phương án C sai.
Do đó phương án D đúng.
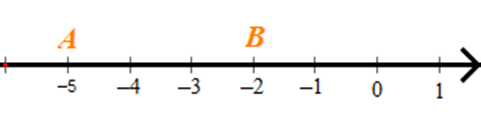
Câu 7. Trên trục số biểu diễn như sau:
Độ dài đoạn thẳng AB là:
A. –3;
B. –7;
C. 3;
D. 7.
Hiển thị đáp án
Đáp án đúng là: C.
Trên trục số, điểm O biểu diễn gốc 0; điểm A biểu diễn số –5; điểm B biểu diễn số –2.
Khi đó OA = |–5| và OB = |–2|.
Ta có |–5| = –(–5) = 5; |–2| = –(–2) = 2.
Khi đó AB = OA – OB = 5 – 2 = 3.
Câu 8. Tìm x biết |x| = 2 3
A. x = 2 3
B. x = - 2 3
C. x = 2 3 2 3
D. Không có giá trị x nào thoả mãn yêu cầu đề bài.
Hiển thị đáp án
Đáp án đúng là: C.
Vì |x| = 2 3 2 3 2 3
Vậy giá trị x thoả mãn x = 2 3 2 3
Câu 9. Tìm tất cả các giá trị x thoả mãn
A. x = 1 2
B. x = - 1 2 ;
C. x = 1 2 x = - 1 2 ;
D. Không có giá trị nào của x thoả mãn.
Hiển thị đáp án
Đáp án đúng là: C.
x = 1 2 x = - 1 2 .
Vậy x = 1 2 x = - 1 2 .
Câu 10. Giá trị của biểu thức A = –|–3,6| : 1,2 là:
A. A = –3;
B. A = 3;
C. A = –0,3;
D. A = 0,3.
Hiển thị đáp án
Đáp án đúng là: A.
A = –|–3,6| : 1,2
A = –[–(–3,6)] : 1,2
A = –[3,6] : 1,2
A = –3.
Vậy A = –3.
Câu 11. Cho biểu thức M = |x + 3,4| – |–1,5|. Khi x = –0,2 thì giá trị của M là:
A. 4,7;
B. 1,7;
C. –4,7;
D. –1,7.
Hiển thị đáp án
Đáp án đúng là: B.
Thay x = –0,2 vào biểu thức M = |x + 3,4| – |–1,5| ta được:
M = |–0,2 + 3,4| – |–1,5|
M = |3,2| – [–(–1,5)]
M = 3,2 – 1,5
M = 1,7.
Vậy khi x = –0,2 thì M = 1,7.
Câu 12. Cho biểu thức
Khi x = –2 thì giá trị của N là:
A. - 33 4 ;
B. 27 4 ;
C. 33 4 ;
D. 59 4 ·
Hiển thị đáp án
Đáp án đúng là: C.
Thay x = –2 vào biểu thức
ta được:
N = | - 6 , 5 | + 7 4
N = 6 , 5 + 7 4
N = 65 10 + 7 4
N = 130 20 + 35 20
N= 165 20
N= 33 4
Câu 13. Tìm số thực dương x biết
A. x = 2 ;
B. x = - 2 ;
C. x = - - 2 ;
D. Không có số thực dương x nào thoả mãn.
Hiển thị đáp án
Đáp án đúng là: D.
x + 2 = 0
x = - 2
Mà x là số thực dương nên x > 0, do đó x = - 2
Vậy không có số thực dương x nào thoả mãn.
Câu 14. Tìm số thực x biết |x – 2021| = –2022.
A. x = 1;
B. x = –1;
C. x = 4043;
D. Không có số thực x nào thoả mãn.
Hiển thị đáp án
Đáp án đúng là: D.
Vì |x – 2021| > 0 với mọi số thực x, mà –2022 < 0.
Vậy không có số thực x nào thoả mãn yêu cầu đề bài.
Câu 15. Có bao nhiêu giá trị x thoả mãn 7,5 – 3.|5 – 2x| = –4,5?
A. 0;
B. 1;
C. 2;
D. 3.
Hiển thị đáp án
Đáp án đúng là: C.
Ta có:
7,5 – 3.|5 – 2x| = –4,5
3.|5 – 2x| = 7,5 –(–4,5)
3.|5 – 2x| = 7,5 + 4,5
3.|5 – 2x| = 12
|5 – 2x| = 12 : 3
|5 – 2x| = 4
Trường hợp 1: 5 – 2x = 4
2x = 5 – 4
2x = 1
x = 1 2
Trường hợp 2: 5 – 2x = –4
2x = 5 – (–4)
2x = 5 + 4
2x = 9
x = 9 : 2
x = 9 2
Vậy có hai giá trị của x thoả mãn là x = 1 2 x = 9 2