Giá trị tuyệt đối của một số thực (Lý thuyết Toán lớp 7) - Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 7 Bài 3: Giá trị tuyệt đối của một số thực hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Giá trị tuyệt đối của một số thực (Lý thuyết Toán lớp 7) - Cánh diều

Lý thuyết Giá trị tuyệt đối của một số thực

1. Khái niệm

- Khoảng cách từ điểm x đến điểm gốc 0 trên trục số được gọi là giá trị tuyệt đối của số x, kí hiệu |x|.

Nhận xét:

- Giá trị tuyệt đối của một số luôn là một số không âm: |x| ≥ 0 với mọi số thực x.

- Hai số thực đối nhau có giá trị tuyệt đối bằng nhau.

Ví dụ:

- Khoảng cách từ điểm 3 đến gốc 0 là 3 nên giá trị tuyệt đối của số 3 là 3, tức là |3| = 3.

- Khoảng cách từ điểm –3 đến gốc 0 là 3 nên giá trị tuyệt đối của số –3 là 3, tức là |–3| = 3.

- Số 3 và –3 là hai số đối nhau, |3| = |–3| = 3.

2. Tính chất

- Nếu x là số dương thì giá trị tuyệt đối của x là chính nó: |x| = x (x > 0).

- Nếu x là số âm thì giá trị tuyệt đối của x là số đối của nó: |x| = – x (x < 0).

- Giá trị tuyệt đối của 0 là 0: |0| = 0.

Nhận xét: Với mỗi số thực x, ta có:

+) $\left|x\right|=\left(\begin{array}{c}xkhi\text{x}\ge \text{0}\\ -x\text{khi x < 0}\end{array}\right)$.

+)|– x| = |x|.

Ví dụ: Tìm |– 76; |3,1|

Vì – 76 < 0 nên |–76| = – (–76) = 76

Vì 3,1 > 0 nên |3,1| = 3,1.

Chú ý: Giả sử hai điểm A, B lần lượt biểu diễn hai số thực a, b khác nhau trên trục số. Khi đó, độ dài của đoạn thẳng AB là |a – b|, tức là AB = |a – b|.

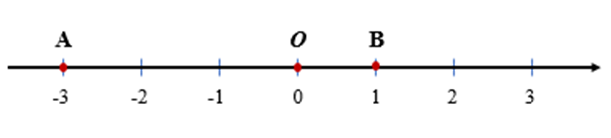
Ví dụ: Tính độ dài đoạn thẳng AB trên hình vẽ sau:
a)

Ta có AB = OA + OB = |–3| + |1| = 3 + 1 = 4.

Hay AB = |–3 – 1| = |–4| = 4.
b)

Ta có AB = OA – OB = |–4| – |–1| = 4 – 1 = 3.

Hay AB = |(–4) – (– 1)| = |– 3| = 3.

Bài tập Giá trị tuyệt đối của một số thực

Bài 1: Tìm |–53|; $\left(-\sqrt{10}\right)$; $\left(\frac{-7}{-9}\right)$.

Hướng dẫn giải

|–53| = –(–53) = 53

$\left(-\sqrt{10}\right)$ = $-\left(-\sqrt{10}\right)$ = $\sqrt{10}$

$\left(\frac{-7}{-9}\right)$ = $\left(\frac{7}{9}\right)$ = $\frac{7}{9}$.

Bài 2: Tính giá trị của biểu thức sau

a) |–100| – |34| ;

b) |12| + 3.|–8|.

Hướng dẫn giải

a) |–100| – |34| = 100 – 34 = 66.

b) |12| + 3. |–8| = 12 + 3.8 = 12 + 24 = 36.

Bài 3: Tìm x biết

a) |x| = 1 ;

b) |x – 3| = – 2 ;

c) |x + 0,5| = 4.

Hướng dẫn giải

a) |x| = 1 nên x = 1 hoặc x = –1.

b) | x – 3| ≥ 0 với mọi số thực x, nên không có số thực x nào thỏa mãn | x – 3| = –2

c) | x + 0,5| = 4 nên x + 0,5 = 4 hoặc x + 0,5 = –4

Với x + 0,5 = 4 thì x = 3,5

Với x + 0,5 = –4 thì x = –5,5.

Bài 4: Tìm độ dài đoạn thẳng AB trong hình vẽ sau:

Hướng dẫn giải

Cách 1: Ta có AB = OA + OB = | –3| + |2| = 3 + 2 = 5

Cách 2 (Dùng chú ý ở trên): Ta có AB = | –3 – 2| = | –5| = 5.

Học tốt Giá trị tuyệt đối của một số thực

Các bài học để học tốt Giá trị tuyệt đối của một số thực Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài 3: Giá trị tuyệt đối của một số thực

• Giải sbt Toán 7 Bài 3: Giá trị tuyệt đối của một số thực