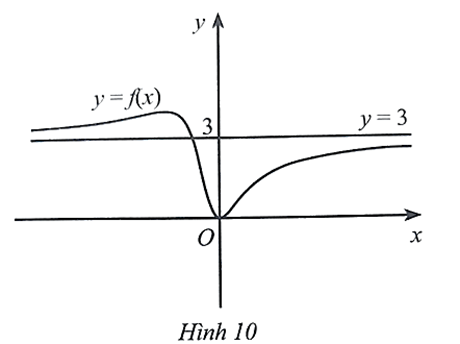
Cho hàm số y = f(x) liên tục trên ℝ và đồ thị có đường tiệm cận ngang như Hình 10

❮ Bài trước Bài sau ❯

Cho hàm số y = f(x) liên tục trên ℝ và đồ thị có đường tiệm cận ngang như . Hàm số y = f(x) có thể là hàm số nào trong các hàm số sau?

Giải SBT Toán 12 Cánh diều Bài 3: Đường tiệm cận của đồ thị hàm số

Bài 56 trang 25 SBT Toán 12 Tập 1: Cho hàm số y = f(x) liên tục trên ℝ và đồ thị có đường tiệm cận ngang như Hình 10. Hàm số y = f(x) có thể là hàm số nào trong các hàm số sau?

A. $f (x) = \frac{3 x^{2}}{x^{2} + x + 1} .$

B. $f (x) = \frac{2 x^{2}}{x^{2} + x + 1} .$

C. $f (x) = \frac{x^{2}}{x^{2} + x + 1} .$

D. $f (x) = \frac{x^{2}}{3 x^{2} + x + 1} .$

Lời giải:

Đáp án đúng là: A

Quan sát Hình 10, ta thấy đường thẳng y = 3 là đường tiệm cận ngang của đồ thị hàm số y = f(x).

Nhận thấy: $\lim_{x \to - \infty}$ $\frac{3 x^{2}}{x^{2} + x + 1}$ = 3; $\lim_{x \to + \infty}$ $\frac{3 x^{2}}{x^{2} + x + 1}$ = 3.

Do đó, đường thẳng y = 3 là đường tiệm cận ngang của đồ thị hàm số y = $\frac{3 x^{2}}{x^{2} + x + 1}$ .

Vậy f(x) = $\frac{3 x^{2}}{x^{2} + x + 1}$ .

Lời giải SBT Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯