Bài 6 trang 73 Toán 10 Tập 1 Chân trời sáng tạo

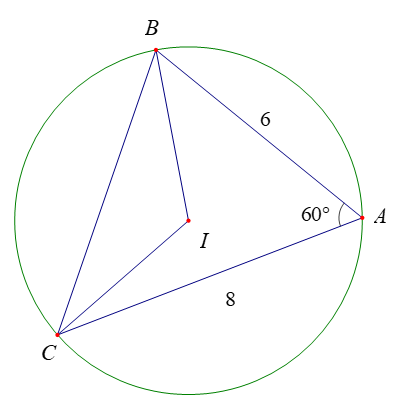
Cho tam giác ABC có AB = 6, AC = 8 và .

Giải Toán lớp 10 Bài 2: Định lí côsin và định lí sin

Bài 6 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 6, AC = 8 và $\hat{A} = 60^{o}$ .

a) Tính diện tích tam giác ABC.

b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.

Lời giải:

a) Áp dụng công thức tính diện tích tam giác ta có:

$S = \frac{1}{2} . A C . A B . \sin A = \frac{1}{2} .6.8. \sin 60^{o} = \frac{1}{2} .6.8. \frac{\sqrt{3}}{2} = 12 \sqrt{3} \approx 20, 8$

Vậy diện tích tam giác ABC là 20,8 (đơn vị diện tích).

b) Áp dụng định lí côsin cho tam giác ABC ta có:

BC² = AB² + AC²– 2.AB.AC.cosA = 6² + 8²– 2.6.8.cos60° = 52

⇒ BC = $\sqrt{52}$ ≈ 7,2.

Mặt khác diện tích tam giác ABC:

$S = \frac{A B . A C . B C}{4 R} \Rightarrow R = \frac{A B . A C . B C}{4 S} = \frac{6.8. \sqrt{52}}{4.12 \sqrt{3}} \approx 4, 2$

Bài 6 trang 73 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán lớp 10

Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên ta có IA = IB = IC = R = 4,2.

Nửa chu vi của tam giác IBC: $p = \frac{I B + I C + B C}{2} = \frac{4, 2 + 4, 2 + 7, 2}{2} = 7, 8$

Áp dụng công thức Heron ta tính được diện tích tam giác IBC:

$S = \sqrt{7, 8. (7, 8 - 4, 2) . (7, 8 - 4, 2) . (7, 8 - 7, 2)} \approx \sqrt{60, 7} \approx 7, 8$

Vậy diện tích tam giác IBC là 7,8 (đơn vị diện tích).

Lời giải bài tập Toán 10 Bài 2: Định lí côsin và định lí sin hay, chi tiết khác: