Hoạt động khám phá 4 trang 70 Toán 10 Tập 1 Chân trời sáng tạo

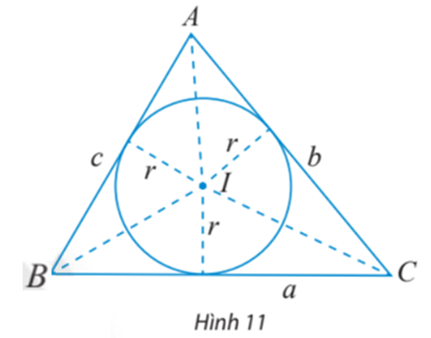
Cho tam giác ABC có BC = a, AC = b, AB = c và (I; r) là đường tròn nội tiếp tam giác (Hình 11).

Giải Toán lớp 10 Bài 2: Định lí côsin và định lí sin

Hoạt động khám phá 4 trang 70 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, AC = b, AB = c và (I; r) là đường tròn nội tiếp tam giác (Hình 11).

Hoạt động khám phá 4 trang 70 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán lớp 10

a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.

b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC:

$S = \frac{r (a + b + c)}{2}$

Lời giải:

a) Diện tích tam giác AIB là $S_{A I B} = \frac{1}{2} \cdot r \cdot A B = \frac{1}{2} \cdot r \cdot c$

Diện tích tam giác AIC là $S_{A I C} = \frac{1}{2} \cdot r \cdot A C = \frac{1}{2} \cdot r \cdot b$

Diện tích tam giác BIC là $S_{B I C} = \frac{1}{2} \cdot r \cdot B C = \frac{1}{2} \cdot r \cdot a$

b) Diện tích tam giác ABC bằng tổng diện tích của ba tam giác AIB, AIC, BIC.

$S = \frac{1}{2} r a + \frac{1}{2} r b + \frac{1}{2} r c = \frac{1}{2} r (a + b + c) = \frac{r (a + b + c)}{2}$

Vậy diện tích tam giác ABC là: $S = \frac{r (a + b + c)}{2}$ .

Lời giải bài tập Toán 10 Bài 2: Định lí côsin và định lí sin hay, chi tiết khác: