Bài 9 trang 73 Toán 10 Tập 1 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

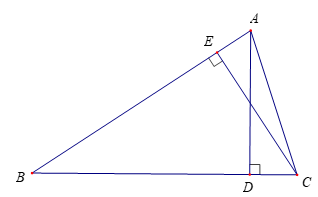
Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.

Giải Toán lớp 10 Bài 2: Định lí côsin và định lí sin

Bài 9 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.

a) Chứng minh $\frac{S_{B D E}}{S_{B A C}} = \frac{B D . B E}{B A . B C}$

b) Biết rằng S_ABC = 9S_BDE và DE = $2 \sqrt{2}$ . Tính cosB và bán kính đường tròn ngoại tiếp tam giác ABC.

Lời giải:

Bài 9 trang 73 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán lớp 10

a) Áp dụng công thức tính diện tích tam giác cho hai tam giác BDE và tam giác ABC ta có:

$S_{B D E} = \frac{1}{2} . B D . B E . \sin B$

$S_{A B C} = \frac{1}{2} . B A . B C . \sin B$

Suy ra $\frac{S_{B D E}}{S_{B A C}} = \frac{\frac{1}{2} B D . B E . \sin B}{\frac{1}{2} B A . B C . \sin B} = \frac{B D . B E}{B A . B C}$

Vậy $\frac{S_{B D E}}{S_{B A C}} = \frac{B D . B E}{B A . B C}$

b) Từ S_ABC = 9S_BDE ⇒ $\frac{S_{B D E}}{S_{B A C}} = \frac{B D . B E}{B A . B C} = \frac{1}{9}$

Tam giác BEC vuông tại E có: cosB = $\frac{B E}{B C}$ .

Tam giác ADB vuông tại D có: cosB = $\frac{B D}{A B}$ .

Suy ra cos²B = $\frac{B E}{B C} . \frac{B D}{A B} = \frac{B D . B E}{B A . B C} = \frac{1}{9} \Rightarrow \cos B = \pm \frac{1}{3}$

Mặt khác, vì góc B nhọn nên sinB > 0, cosB > 0, do đó: cosB = $\frac{1}{3}$

Mà sin²B + cos²B = 1, suy ra sinB = $\sqrt{1 - \cos^{2} B} = \sqrt{1 - {(\frac{1}{3})}^{2}} = \frac{2 \sqrt{2}}{3}$

Xét hai tam giác BDE và tam giác BAC có:

$\frac{B E}{B C} = \frac{B D}{A B} = \frac{1}{3}$ (cùng bằng cosB)

Góc B chung

Suy ra hai tam giác BDE và tam giác BAC đồng dạng theo hệ số tỉ lệ k = $\frac{1}{3}$

⇒ $\frac{D E}{A C} = \frac{1}{3} \Rightarrow A C = 3 D E = 3.2 \sqrt{2} = 6 \sqrt{2}$

Áp dụng định lí sin cho hai tam giác BAC và tam giác BDE ta có:

$\frac{A C}{\sin B} = 2 R$ ; $\frac{D E}{\sin B} = 2 R' \Rightarrow R' = \frac{D E}{2 \sin B} = \frac{2 \sqrt{2}}{2. \frac{2 \sqrt{2}}{3}} = \frac{3}{2}$ (R’ là bán kính đường tròn ngoại tiếp tam giác BDE).

⇒ $\frac{R}{R'} = \frac{A C}{D E} = \frac{6 \sqrt{2}}{2 \sqrt{2}} = 3$ ⇒ R = 3R' = $3. \frac{3}{2} = \frac{9}{2}$

Vậy cosB = $\frac{1}{3}$ ; R = $\frac{9}{2}$

Lời giải bài tập Toán 10 Bài 2: Định lí côsin và định lí sin hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯