Hoạt động khám phá 2 trang 67 Toán 10 Tập 1 Chân trời sáng tạo
Giải Toán lớp 10 Bài 2: Định lí côsin và định lí sin
Hoạt động khám phá 2 trang 67 Toán lớp 10 Tập 1:
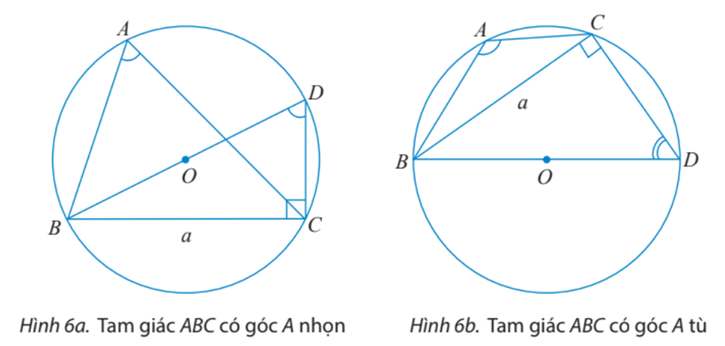
a) Cho tam giác ABC không phải là tam giác vuông có BC = a, AC = b; AB = c và R là bán kính đường tròn ngoại tiếp tam giác đó. Vẽ đường kính BD.
i) Tính sin theo a và R.
ii) Tìm mối liên hệ giữa hai góc và . Từ đó chứng minh rằng 2R = .
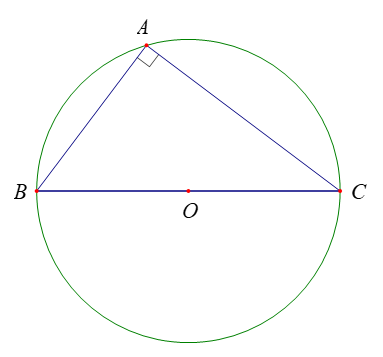
b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức 2R = .
Lời giải:
a)
i) Do BD là đường kính của đường tròn nên tam giác BCD vuông tại C.
⇒ sin =
Vậy sin = .
ii)
+) Trường hợp tam giác ABC có góc A nhọn:
Hai góc và là hai góc nội tiếp cùng chắn , do đó
Suy ra sin = sin =
⇒ 2R = , tức là 2R =
Vậy 2R =
+) Trường hợp tam giác ABC có góc A tù:
Tứ giác ABDC nội tiếp đường tròn tâm O nên ta có =180°;
⇒ = 180° – ;
⇒ sin = sin(180o – )= sin ;
⇒ sin = sin =
⇒ 2R = , tức là 2R =
Vậy 2R = .
b) Với tam giác ABC vuông tại A. Khi đó BC sẽ là đường kính của đường tròn ngoại tiếp tam giác ABC nên BC = 2R.
⇒ sinA = sin90° = 1 và .
Vậy tam giác ABC vuông tại A thì ta vẫn có công thức 2R = .
Lời giải bài tập Toán 10 Bài 2: Định lí côsin và định lí sin hay, chi tiết khác: