Bài tập về tính công, công suất của nguồn điện nâng cao cực hay

---

Bài tập về tính công, công suất của nguồn điện nâng cao cực hay

Với Bài tập về tính công, công suất của nguồn điện nâng cao cực hay Vật Lí lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập từ đó đạt điểm cao trong bài thi môn Vật Lí 9.

Bài tập ví dụ minh họa

Bài 1: Cho mạch điện như hình vẽ. Cho biết hiệu điện thế U = 24V.

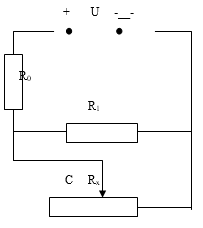
Các điện trở R₀ = 6 Ω, R₁ = 18 Ω, R_x là một biến trở, dây nối có điện trở không đáng kể.

a) Tính R_x sao cho công suất tiêu hao trên R_x bằng 13,5W và tính hiệu suất của mạch điện. Biết rằng năng lượng điện tiêu hao trên R₁ và R_x là có ích, trên R₀ là vô ích.

b) Với giá trị nào của R_x thì công suất tiêu thụ trên R_x đạt cực đại? Tính công suất cực đại này.

Hướng dẫn giải:

a) Điện trở tương đương của R₁ và R_x:

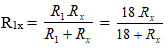
Điện trở toàn mạch: R = R₀ + R_1x

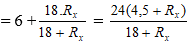
Cường độ dòng điện qua mạch chính:

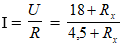
Ta có: I_x.R_x = I.R_1x

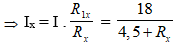
Công suất hao phí trên R_x:

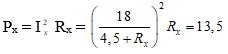
Ta có phương trình bậc 2: R_x² - 15R_x + 20,25 = 0

Giải phương trình bậc 2 ta được 2 nghiệm R_x = 13,5 Ω và R_x = 1,5 Ω.

Hiệu suất của mạch điện:

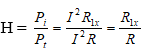
+ Với R_x = 13,5 Ω ta có:

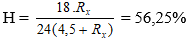
+ Với R_x = 1,5 Ω ta có:

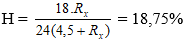
b) Công suất tiêu thụ trên R_x:

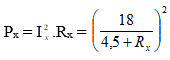
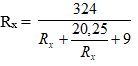
Để P_X cực đại thì mẫu số phải cực tiểu, nhưng tích của 2 số không âm:

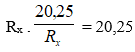
→ tổng của chúng sẽ cực tiểu khi:

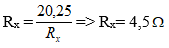
Lúc đó giá trị cực đại của công suất:

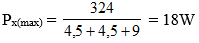
Bài 2: Cho mạch điện (như hình vẽ):

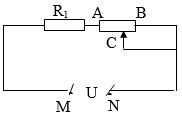
AB làm biến trở con chạy C có điện trở toàn phần là 120Ω. Nhờ có biến trở làm thay đổi cường độ dòng điện trong mạch từ 0.9A đến 4.5A.

1. Tìm giá trị của điện trở R₁ ?

2. Tính công suất toả nhiệt lớn nhất trên biến trở.

Biết U không đổi.

Đáp án: a) R₁ = 30 Ω; b) R_x = 30 Ω; P_max = 151,875 W.

Hướng dẫn giải:

I_min = 0,9 A mà U không đổi ⇒ R_{tđ max}

⇒ C ≡ B và R_tđ = R₁ + R_AB = R₁ + 120 (Ω)

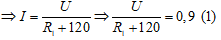
Khi I_max = 4,5A; U không đổi ⇒ R_{tđ min} ⇒ C ≡ A để R_AC = 0 khi đó R_tđ = R₁.

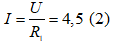
Từ (2) Ta có: U = 4,5 R₁ (3).

Thế (3) vào (1) ta có:

⇔ 4,5R₁ = 0,9R₁ + 108

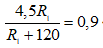
⇔ 3,6R₁ = 108 ⇔ R₁ = 30Ω ⇒ U = 135V

Vậy R₁ = 30Ω và U = 135 V

2, Tìm vị trí của C để P_x đạt giá trị lớn nhất ?

Gọi R_AC = R_x (Ω) (0 < R_x < 120) để P_x đạt giá trị lớn nhất?

Khi đó công suất toả nhiệt: P_x = R_x.I²

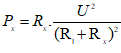
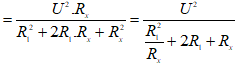
Để P_x đạt giá trị lớn nhất ⇔ nhỏ nhất.

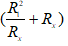
Áp dụng bất đẳng thức Cô si vào 2 số dương ta có:

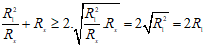
Nghĩa là: giá trị nhỏ nhất là 2R₁, thay R₁ = 30(Ω)

Ta có phương trình:

⇔ R_x² - 60R_x + 900 = 0 ⇔ R_x = 30Ω

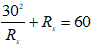
Khi đó P_x (cực đại) là:

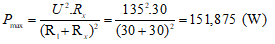
Bài 3: Cho mạch điện (như hình vẽ).

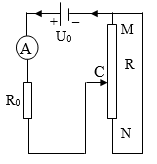
Biết U_o = 12 V, R_o là điện trở, R là biến trở ampe kế lí tưởng. Khi con chạy C của biến trở R từ M đến N, ta thấy ampe kế chỉ giá trị lớn nhất I₁ = 2A. Và giá trị nhỏ nhất I₂ = 1A. Bỏ qua điện trở của các dây nối.

1 – Xác định giá trị R_o và R ?

2 – Xác định vị trí của con chạy C của biến trở R để công suất tiêu thụ trên toàn biến trở bằng một nửa công suất cực đại của nó ?

Đáp án:

Hướng dẫn giải:

1. Với mạch điện này thì: R_MC // R_NC và R_MC + R_NC = R .

Vì vậy khi ta đặt R_MC = x (Ω) ⇒ R_NC = R – x (0 < x < R)

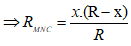
Khi đó chỉ số của am pe kế là:

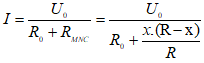
+) Khi con chạy C ở M (ở N) thì R_MNC = 0 và lúc đó ampe kế sẽ chỉ giá trị cực đại:

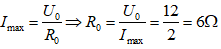
+) Để am pe kế chỉ giá trị nhỏ nhất thì: phải có giá trị cực đại, ta triển khai R_CNM:

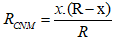
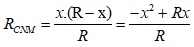
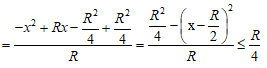
Để R_MNC có giá trị cực đại bằng R/4 thì:

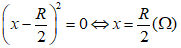
Tức là con chạy C ở chính giữa của biến trở và

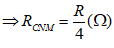
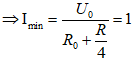
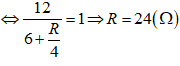
2 - Để có phương án giải phần này ta phải áp dụng công thức P = I²R và định luật bảo toàn năng lượng trên toàn mạch điện .

Đặt

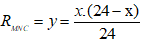
mà P_MNC = R_MNC.I²

Công suất tiêu thụ trên toàn biến trở là:

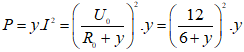
Mà công suất của nguồn điện và công suất tiêu thụ trên R₀ là P_n = U_oI và P_Ro = R_o.I²

Theo định luật bảo toàn năng lượng ta có: P_n = P_Ro + P hay U_oI = R_o.I² + P

⇒ R₀.I² – U₀.I + P = 0 (*)

(*) là phương trình bậc 2 với ẩn là I

Để phương trình có nghiệm: Δ ≥ 0

⇒ Δ = U² - 4R₀.P ≥ 0

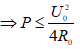
Vậy

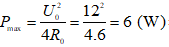
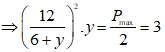
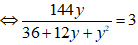
⇔ 144y = 108 + 36y + 3y²

⇔ 3y² - 108y + 108 = 0

⇔ y² - 36y + 36 = 0

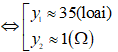
Mà ta đặt nên ta có phương trình:

⇒ x² - 24x + 24 = 0

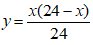
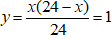
Giải phương trình trên ta có x₁ = 1 Ω; x₂ = 23 Ω.

Vậy có 2 vị trí của con chạy C trên biến trở R sao cho R_MC = 1 Ω hoặc R_MC = 23 Ω thì công suất tiêu thụ trên toàn biến trở bằng một nửa công suất cực đại của nó.

Bài tập trắc nghiệm tự luyện

Bài 1: Cho mạch điện như hình vẽ. Biến trở AB là một dây dẫn đồng chất, chiều dài l = 1,3 m, tiết diện thẳng S = 0,1 mm², điện trở suất ρ = 10^-6 Ω.m. U là hiệu điện thế không đổi. Di chuyển con chạy C ta nhận thấy khi ở các vị trí cách đầu A một đoạn 10 cm hoặc cách đầu B một đoạn 40 cm thì công suất toả nhiệt trên biến trở là như nhau.

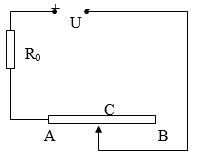
a) Xác định giá trị của R₀.

b) Gọi công suất tỏa nhiệt trên R₀ ứng với 2 vị trí của con chạy C kể trên lần lượt là P₁ và P₂. Tìm tỷ số P₁/P₂.

Hiển thị đáp án

Áp dụng công thức tính điện trở

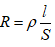
- Khi C ở cách đầu A đoạn 10 cm và cách B đoạn 40 cm thì điện trở của biến trở tham gia vào mạch điện lần lượt là: R₁ = 1 Ω, R₂ = 9 Ω.

- Công suất tỏa nhiệt trên biến trở ứng với hai vị trí trên là:

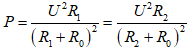
⇒ R₀ = 3 Ω

Công suất tỏa nhiệt trên R₀ tương ứng là:

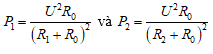
⇒ Tỷ số:

Bài 2: Cho mạch điện như hình vẽ.

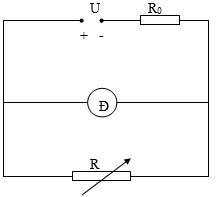
Đèn Đ có ghi: 6 V – 3 W. Thay đổi biến trở R để công suất trên nó đạt giá trị cực đại và bằng 9 W, khi đó đèn sáng bình thường. Tìm giá trị của R₀ và U. Bỏ qua điện trở của dây nối.

Hiển thị đáp án

Điện trở của đèn là: R_đ = 12 Ω, đặt R = x.

Điện trở tương đương của mạch:

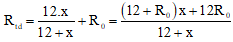
Cường độ dòng điện trong mạch:

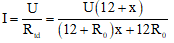
Cường độ dòng điện qua biến trở:

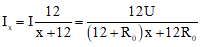
Công suất trên biến trở:

⇒

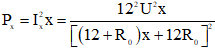
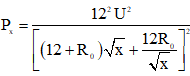
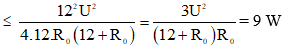
⇒ U² = 3.R₀(12 + R₀) (1)

Dấu “ = ” xảy ra khi

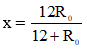
Khi đèn sáng bình thường thì hiệu điện thế hai đầu biến trở bằng hiệu điện thế hai đầu đèn bằng 6 V

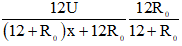
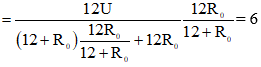
Hay: U = 12 + R₀ (2)

Từ (1) và (2) suy ra: R₀ = 6 Ω và U = 18 V.

Đáp án: R₀ = 6 Ω và U = 18 V.

Bài 3: Cho mạch điện như hình vẽ. Nguồn điện có hiệu điện thế không đổi U = 8V, Đ là bóng đèn (3V - 3W) có điện trở R₁, các điện trở r = 2Ω, R₂ = 3Ω, MN là một biến trở có điện trở toàn phần bằng 3Ω, ampe kế, khóa K và các dây nối có điện trở không đáng kể, coi điện trở của bóng đèn không phụ thuộc vào nhiệt độ.

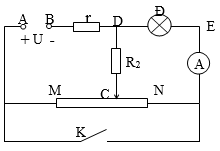
1. Mở khóa K. Điều chỉnh vị trí của con chạy C sao cho RCN = 1Ω.

Tìm R₁, R_AB và số chỉ của Ampe kế khi đó.

2. Đóng khóa K

a) Xác định vị trí của con chạy C để công suất tiêu thụ trên biến trở bằng 0,6 W.

b) Xác định vị trí của con chạy C để công suất tiêu thụ trên bóng đèn cực đại.

Hiển thị đáp án

1. Tìm số chỉ của Ampe kế khi K mở

Sơ đồ mạch: R_MC nt (R₂ // (R_CN nt R₁)) nt r

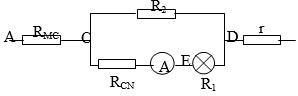
Ta có: R_CN = 1Ω; R_CM = 2Ω; R₁ = 3Ω

R_CED = R_CN + R₁ = 4Ω

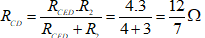
Điện trở tương đương của mạch điện:

R_AB = R_MC + R_CD + r

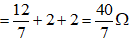
Cường độ dòng điện trong mạch chính:

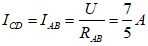
U_CD = U_CED = I_CD.R_CD

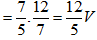
Số chỉ Ampe kế:

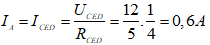
2. K đóng

a. Sơ đồ mạch điện: (((R_CN // R_CM) nt R₂) // R₁) nt r

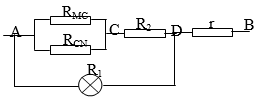
Đặt R_CN = x (O ≤ x ≤ 3) ⇒ R_MC = 3 - x; R_AC = y (0 ≤ y ≤ 3)

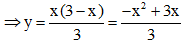
R_ACD = R₂ + R_AC = y + 3

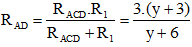
R_AB = r + R_AD

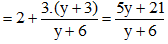
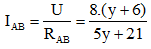
Ta có: U_AD = I_AB.R_AD

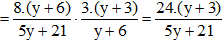
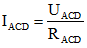
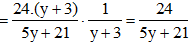
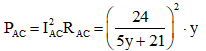
Để công suất tiêu thụ trên biến trở bằng 0,6 W thì:

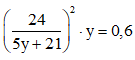
⇒ y = 3/5 ⇒ x ≈ 2,17 Ω hoặc x ≈ 0,83Ω

b. Công suất tiêu thụ trên đèn cực đại khi U_AD max

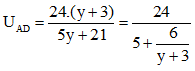
Khi y tăng thì (y + 3) tăng giảm ⇒ U_AD tăng

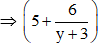
Như vậy U_AD lớn nhất khi y lớn nhất.

Ta có:

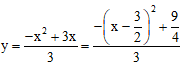
Ta có:

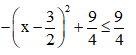
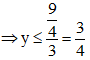
⇒ y_max = 3/4 khi x = 3/2 Ω

Bài 4: Một biến trở có giá trị điện trở toàn phần R = 120 Ω. Nối tiếp với một điện trở R₁. Nhờ biến trở có thể làm thay đổi cường độ dòng điện trong mạch từ 0,9A đến 4,5 A.

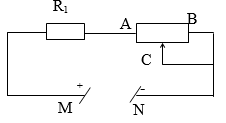
a) Tính giá trị của điện trở R₁

b) Tính công suất toả nhiệt lớn nhất trên biến trở. Biết rằng mạch điện được mắc vào mạch điện có hiệu điện thế U không đổi

Hiển thị đáp án

a) Cường độ dòng điện lớn nhất khi con chạy C ở vị trí A. và nhỏ nhất khi con chạy C ở vị trí B của biến trở

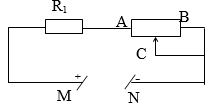
Ta có:

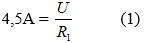
Và

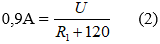
Từ (1) và (2) ta có: R₁ = 30 Ω; U = 135V

b) Gọi Rx là phần điện trở từ A → C trên biến trở

Công suất toả nhiểt trên Rx là:

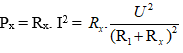
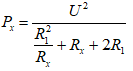
Để P_x đạt giá trị cực đại ta phải có: đạt cực tiểu.

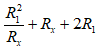
Vì 2R₁ không đổi nên cần đạt cực tiểu.

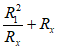
Nên ta có:

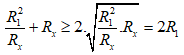
(bất đẳng thức Cô Si)

Do đó đạt cực tiểu bằng 2.R₁ hay

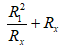
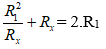
⇒ R₁² + R_x² = 2.R₁.R_x

⇔ (R₁ - R_x)² = 0 ⇔ R₁ = R_x = 30 Ω

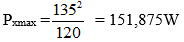
Đáp án: R₁ = 30Ω; P_{x max} = 151,875 W

Bài 5: Cho sơ đồ như hình vẽ. R = 4 Ω; R₁ là đèn 6V – 3W; R₂ là biến trở; U_MN không đổi bằng 10V.

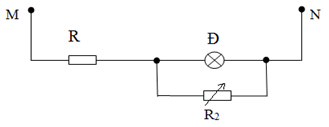
a) Xác định R₂ để đèn sáng bình thường.

b) Xác định R₂ để công suất tiêu thụ của R₂ là cực đại.

c) Xác định R₂ để công suất tiêu thụ của mạch song song cực đại.

Hiển thị đáp án

a) Khi đèn sáng bình thường thì:

U_R2 = U_Đ = 6 V;

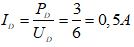
U_R = U_MN – U_Đ = 10 – 6 = 4 (V)

Cường độ dòng điện trong mạch chính là:

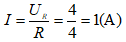
Suy ra: I₂ = I – I_D = 1 - 0,5 = 0,5 (A).

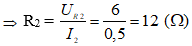
b) Tính R_MN theo R₂; I theo R₂ và I₂ theo R₂ ta có: P₂ = I₂².R₂.

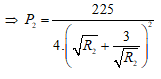
⇒ P₂ cực đại khi R₂ = 3 Ω.

c) Đặt điện trở tương đương của đoạn mạch song song là x thì công suất tiêu thụ của đoạn mạch này là:

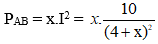
Khi đó: P_AB cực đại khi x = 4. Vậy: R₂ = 6 Ω.

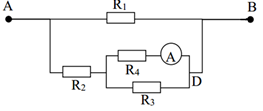
Bài 6: Cho mạch điện như hình vẽ (Hình 3). U_AB = 90V; R₁ = 40 Ω; R₂ = 90Ω; R₄ = 20Ω; R₃ là một biến trở. Bỏ qua điện trở của ampe kế, dây nối và khoá K.

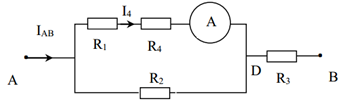
a) Khi mở khóa K và điều chỉnh cho R₃ = 30Ω. Tính điện trở tương đương của đoạn mạch AB và số chỉ của ampe kế.

b) Tìm R₃ để số chỉ của ampe kế khi K mở bằng 3 lần số chỉ của ampe kế khi K đóng.

c) Khi K đóng. Tìm R₃ để công suất tiêu thụ trên R₃ đạt cực đại. Tính công suất cực đại đó.

Hiển thị đáp án

a, Khi K mở đoạn mạch được vẽ lại:

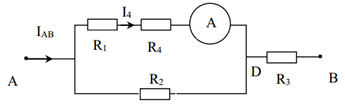
R_AB = R_AD + R₃ =

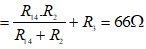
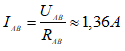
U_AD = I_AB.R_AD = 48,96 V

+ Số chỉ của ampe kế khi khoá K mở

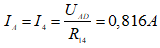
b) Tìm R₃ để số chỉ của ampe kế khi K mở bằng 3 lần số chỉ của ampe kế khi K đóng.

Ta có: khi K mở:

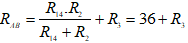
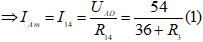
Khi K đóng:

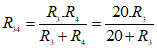
⇒ R₂₃₄ = R₂ + R₃₄

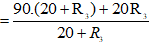
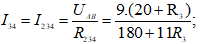
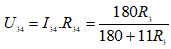
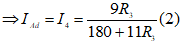
Từ (1) và (2): I_Am = 3I_Ad ⇒ R₃² + 14R₃ - 360 = 0

Suy ra: R₃ ≈ 13,2 Ω (loại nghiệm âm).

c) Ta có:

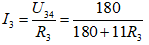
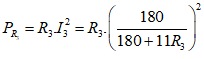
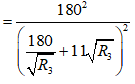
Áp dụng Cosi cho mẫu số, ta được

P_R3 đạt cực đại khi R₃ = 180/11 ≈ 16,4 Ω

Khi đó P_R3 ≈ 4,1 W.

Bài 7: Cho mạch điện như hình vẽ. U_AB = 9V, R₀ = 6 Ω. Đèn Đ thuộc loại 6V - 6W, Rx là biến trở. Bỏ qua điện trở của Ampekế và dây nối.

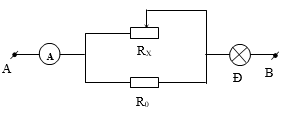
a) Muốn đèn sáng bình thường thì R_x phải có giá trị bao nhiêu?

b) Thay đổi biến trở R_x có giá trị bằng bao nhiêu thì công suất tiêu thụ trên biến trở đạt giá trị lớn nhất. Tính số chỉ của Ampe kế khi đó.

Hiển thị đáp án

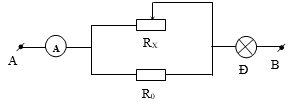
a. Ta có: U_đ = 6V, I_đ = 1A ⇒ R_đ = 6Ω

- Ta có:

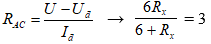
- Tính được: R_x = 6 Ω

b. Ta có:

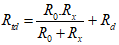
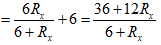
- Suy ra:

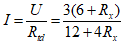
Ta có:

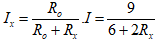
- Tính được:

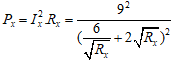
Ta có P_x cực đại khi đạt cực tiểu.

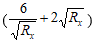
Điều đó xảy ra khi

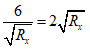
⇒ R_x = 3 Ω

Khi đó:

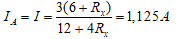
Đáp án:

a) R_x = 6 Ω

b) R_x = 3 Ω; I_A = 1,125 A.

Khi đó U_{NA min} = 6944,2 V

Bài 8: Cho mạch điện như hình 3. Nguồn điện không đổi có hiệu điện thế U = 9V. Đèn Đ₁ ghi 3V - 3W; Đ₂ ghi 9V - 6,75W; Đ₃ ghi 9V - 13,5W; Đ₄ ghi 3V - 1,5W. Biết rằng đèn sẽ bị cháy nếu hiệu điện thế đặt vào nó vượt quá 35% hiệu điện thế định mức. Bỏ qua điện trở ở tiếp điểm của các khóa K₁, K₂ và dây nối. Ban đầu, các khóa K₁ và K₂ đều mở. Xác định độ sáng của các đèn trong trường hợp:

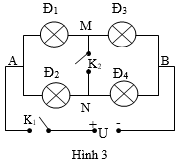
a) K₁ đóng, K₂ mở.

b) K₁ đóng, K₂ đóng.

Hiển thị đáp án

Điện trở và các thông số định mức của mỗi đèn có giá trị như sau:

Đèn	UĐm	PĐm	IĐm	R
Đ1	3V	3W	1A	3Ω
Đ2	9V	6,75W	0,75A	12Ω
Đ3	9V	13,5W	1,5A	6Ω
Đ4	3V	1,5W	0,5A	6Ω

a) Khi K₁ đóng, K₂ mở.

* Giả sử không có đèn nào bị cháy, mạch có dạng: (Đ₁ nt Đ₃) // (Đ₂ nt Đ₄)

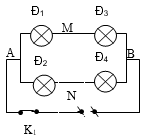
R₁₃ = R₁ + R₃ = 9(Ω);

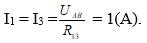
Đ₁ sáng bình thường, Đ₃ sáng yếu.

R₂₄ = R₂ + R₄ = 18(Ω);

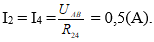
Đ₂ sáng yếu, Đ₄ sáng bình thường.

Chứng tỏ không có đèn nào cháy.

Vậy: Đ₁ sáng bình thường, Đ₂ sáng yếu, Đ₃ sáng yếu, Đ₄ sáng bình thường.

b) Khi K₁ đóng, K₂ đóng.

* Giả sử không có đèn nào bị cháy, mạch có dạng: (Đ₁ // Đ₂) nt (Đ₃ // Đ₄)

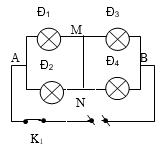
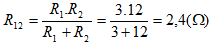
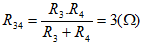
R_td = R₁₂ + R₃₄ = 2,4 + 3 = 5,4 Ω

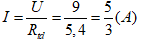
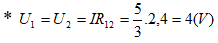
Ta thấy:

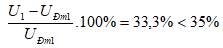
⇒ Đ₁ sáng quá mức bình thường nhưng chưa bị cháy.

+ U₂ < U_Đm2 ⇒ Đ₂ sáng yếu.

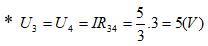
Ta thấy: U₃ < U_Đm3 ⇒ Đ₃ sáng yếu.

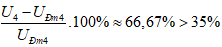
⇒ Đ₄ cháy.

Khi đó mạch điện còn 3 đèn mắc theo dạng: (Đ₁ // Đ₂) nt Đ₃

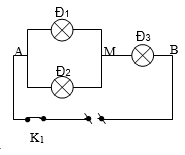
R_td = R₁₂ + R₃ = 2,4 + 6 = 8,4 Ω

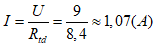
U₁ = U₂ = I.R₁₂ = 1,07.2,4 = 2,57(V) ⇒ Đ₁, Đ₂ sáng yếu.

U₃ = U - U₁ = 9 - 2,57 = 6,43(V) ⇒ Đ₃ sáng yếu.

Vậy: Đ₁ sáng yếu, Đ₂ sáng yếu, Đ₃ sáng yếu, Đ₄ không sáng(bị cháy).

Bài 9: Cho mạch điện như hình vẽ. Hiệu điện thế U giữa hai điểm A và B không đổi. Các điện trở R₂ = R₃ = R₄ = R; R₁ = 3R; Rx là biến trở.

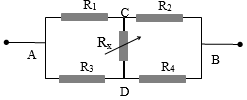
a) Điều chỉnh biến trở R_x đến giá trị sao cho công suất tỏa nhiệt trên điện trở R₁ là P₁ = 12W. Tính công suất tỏa nhiệt trên điện trở R₄ khi đó.

b) Tính giá trị của R_x theo R để công suất tỏa nhiệt trên R_x là lớn nhất.

Hiển thị đáp án

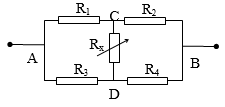
a) Ta có: I₁ + I₃ = I₂ + I₄

⇒ R_I1 + R_I3 = R_I2 + R_I4 (1)

Lại có: U₁ + U₂ = U₃ + U₄

⇒ 3R_I1 + R_I2 = R_I3 + R_I4 (2)

Từ (1) và (2), cộng vế ta có: 4R_I1 = 2R_I4 ⇒ I₄ = 2I₁

Ta có:

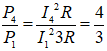
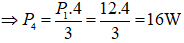
Vậy P₄ = 16W

b) Giả sử dòng điện qua Rx có chiều từ D tới C

Tại C ta có I₂ = I₁ + I_x

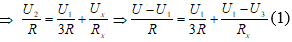
Tại D ta có I₃ = I₄ + I_x

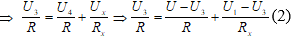
Từ (1) và (2), biến đổi ra hệ phương trình sau:

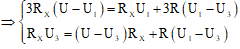
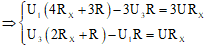
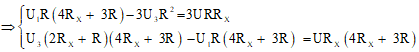
Cộng vế ta được:

⇒ U₃(8R_x² + 10RR_x) = 6U_RRx + 4UR_x² ⇒ U₃(4Rx + 5R) = U(3R + 2Rx)

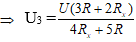
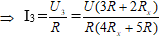
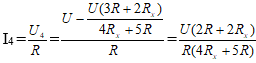
Tại D ta có:

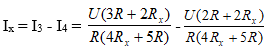
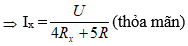
Có:

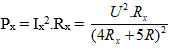
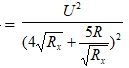
Để P_max thì min

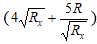
Ta thấy (không đổi)

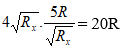
Áp dụng hệ quả Bđt Côsi có min khi

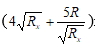
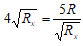
⇒ R_x = 1,25R

Vậy khi R_x = 1,25R thì công suất tiêu thụ trên R_x là lớn nhất.

Bài 10: Cho mạch điện như hình vẽ: U_AB = 12V; r = 6Ω. Đèn Đ ghi 9V – 9W. Cho rằng điện trở của đèn không thay đổi theo nhiệt độ.

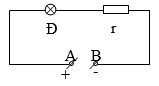
1) Nhận xét về độ sáng của đèn và giải thích.

2) Người ta mắc thêm một điện trở R_x nối tiếp hoặc song song với điện trở r. Nêu cách mắc và tính giá trị của R_x để:

a) Đèn sáng bình thường.

b) Công suất tiêu thụ của nhóm điện trở r và R_x lớn nhất. Tính công suất lớn nhất đó.

Hiển thị đáp án

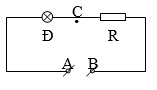
1. Điện trở của đèn

R_td = R + r = 15Ω

→ đèn sáng yếu.

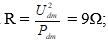
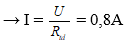
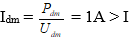
2. a) Gọi R' là điện trở tương đương đoạn mạch r và R_x.

Đèn sáng bình thường nên U_AC = U_dm = 9V → U_CB = 12 – 9 = 3V.

I = I_dm = 1A

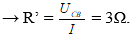
R' < r → phải mắc R_x song song r và R_x = 6Ω

b)

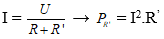
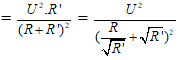
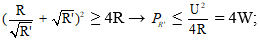
Dấu “=” xảy ra ⇔ R' = R = 9Ω

R' > r → R_x nối tiếp r và R_x = 3Ω thì công suất đoạn r, R_x lớn nhất bằng 4W