Bài tập về mắt lão và cách giải

Bài tập về mắt lão và cách giải

Với Bài tập về mắt lão và cách giải Vật Lí lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập từ đó đạt điểm cao trong bài thi môn Vật Lí 9.

I. Lý thuyết chung về mắt

1. Cấu tạo của mắt

- Mắt là một cơ quan của cơ thể giúp chúng ta nhìn thấy mọi vật.

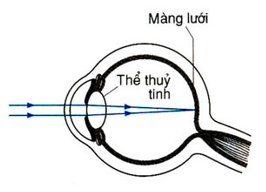
- Hai bộ phận quan trọng nhất của mắt là thể thủy tinh và màng lưới (còn gọi là võng mạc).

+ Thể thủy tinh có tác dụng như một thấu kính hội tụ, nó là một khối chất trong suốt và mềm, dễ dàng phồng lên hay dẹt xuống khi cơ vòng đỡ nó bóp lại hay dãn ra làm cho tiêu cự của nó thay đổi.

+ Màng lưới là một màng ở đáy mắt, tại đó ảnh của vật mà ta nhìn thấy sẽ hiện lên rõ nét. Khi có ánh sáng tác dụng lên màng lưới thì sẽ xuất hiện “luồng thần kinh” đưa thông tin về ảnh lên não.

2. So sánh mắt và máy ảnh

- Về phương diện quang học, mắt giống như một máy ảnh, tạo ra ảnh thật, nhỏ hơn vật trên màng lưới:

+ Thể thủy tinh đóng vai trò như vật kính trong máy ảnh.

+ Màng lưới có tác dụng như màn hứng ảnh.

- Tuy nhiên, ở mắt thì thể thủy tinh có thể thay đổi được tiêu cự. Còn vật kính ở máy ảnh thì không thay đổi được tiêu cự.

3. Sự điều tiết của mắt

- Khi nhìn rõ một vật thì ảnh của vật đó sẽ hiện rõ nét trên màng lưới.

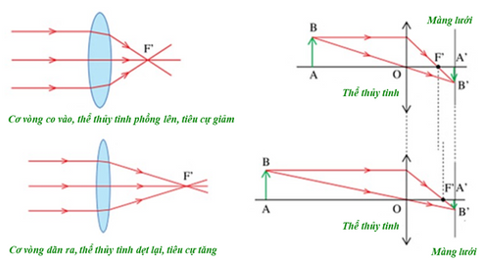
- Khoảng cách từ thể thủy tinh đến màng lưới là cố định, vì vậy mắt phải điều tiết để làm thay đổi tiêu cự của thể thủy tinh. Để điều tiết, cơ vòng đỡ thể thủy tinh sẽ phải co dãn khiến thể thủy tinh phồng lên hoặc dẹt lại, làm thay đổi tiêu cự của nó. Sự điều tiết xảy ra hoàn toàn tự nhiên.

4. Điểm cực cận và điểm cực viễn của mắt

- Điểm cực cận (kí hiệu là C_c ): là điểm gần mắt nhất mà khi có vật ở đó, mắt còn có thể nhìn rõ vật (khi điều tiết tối đa). Khoảng cách từ mắt đến điểm cực cận được gọi là khoảng cực cận.

- Điểm cực viễn (kí hiệu là C_v ): là điểm xa mắt nhất mà khi có vật ở đó, mắt không phải điều tiết mà vẫn có thể nhìn rõ vật. Khoảng cách từ mắt đến điểm cực viễn được gọi là khoảng cực viễn.

- Mắt chỉ có thể nhìn rõ các vật trong khoảng từ điểm cực cận đến điểm cực viễn của mắt. Khoảng cách từ điểm cực cận đến điểm cực viễn gọi là giới hạn nhìn rõ của mắt.

- Mắt bình thường của con người có khả năng nhìn rõ từ khoảng cách 20 cm cho đến vô cùng.

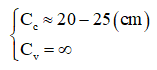
II. Các dạng bài tập

Dạng 2. Bài tập về mắt lão

1. Lý thuyết liên quan tới mắt cận và cách khắc phục

1.1. Những biểu hiện của tật lão thị

- Mắt lão là mắt của người già. Lúc đó cơ vòng đỡ thể thủy tinh đã yếu nên khả năng điều tiết kém hẳn đi.

- Mắt lão nhìn rõ những vật ở xa, nhưng không nhìn rõ những vật ở gần như hồi còn trẻ.

- Điểm cực cận C_c của mắt lão xa mắt hơn so với mắt bình thường.

Ví dụ: Khi đọc sách phải đặt sách xa mắt hơn bình thường;…

1.2. Cách khắc phục tật lão thị

Mắt lão phải đeo kính lão để nhìn rõ các vật ở gần. Kính lão là thấu kính hội tụ.

2. Phương pháp giải

- Vẽ hình minh họa sự tạo ảnh và xác định các đại lượng đề bài đã cho và cần tính.

- Sử dụng các kiến thức hình học để tính các đại lượng đề bài yêu cầu.

- Đối với những bài tập chỉ đề cập đến các dữ kiện liên quan đến kính lão thì ta giải bài tập đó giống với những bài tập về thấu kính hội tụ tạo ảnh ảo.

Áp dụng công thức thấu kính hội tụ với ảnh ảo: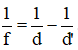

- Đối với những bài tập liên quan đến cả các dữ kiện về mắt, thì ta có thể chia bài toán thành hai giai đoạn:

+ Giai đoạn tạo ảnh ảo của vật bằng kính lão (TKHT)

Áp dụng công thức thấu kính hội tụ với ảnh ảo: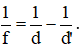

+ Giai đoạn mắt “nhìn” ảnh ảo tạo bởi kính lão (Tạo ảnh thật trên màng lưới bằng TKHT)

Áp dụng công thức thấu kính hội tụ với ảnh thật: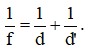

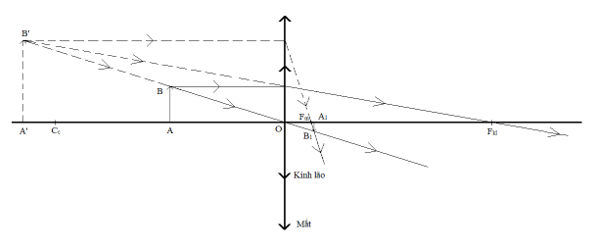
3. Ví dụ

Ví dụ 1: Một người có khả năng nhìn rõ các vật cách mắt từ 50 cm. Hỏi mắt người đó bị vấn đề gì?

A. Mắt người đó không có vấn đề gì.

B. Mắt người đó bị tật cận thị.

C. Mắt người đó bị tật viễn thị.

D. Cả 3 ý trên đều sai.

Lời giải:

Mắt bình thường có điểm cực cận C_c ≈ 20 - 25(cm). Mắt người này có C_c = 50cm => Người này bị viễn thị => chọn C

Ví dụ 2: Một người có khả năng nhìn rõ các vật cách mắt từ 50 cm. Biết khoảng cách từ thể thủy tinh đến màng lưới là 2 cm. Tìm khoảng tiêu cự của mắt đó.

Lời giải:

Áp dụng công thức thấu kính hội tụ với ảnh thật: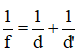

Theo giả thiết, d^' = 2 cm

+ Cực viễn của mắt ở vô cùng => f_∞ = d^' = 2 cm

+ Tại cực cận của mắt: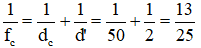

=>

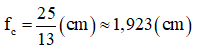
Vậy khoảng tiêu cự của mắt đó là f_c ≤ f ≤ f_∞ hay 1,923 (cm) ≤ f ≤ 2(cm)

III. Bài tập tự luyện

Bài 1: Về phương diện quang học, thể thủy tinh của mắt giống như:

A. Gương cầu lồi

B. Gương cầu lõm

C. Thấu kính hội tụ

D. Thấu kính phân kì

Lời giải: chọn C

Bài 2: A có khoảng nhìn thấy từ 20 cm đến 120 cm, B có khoảng nhìn thấy từ 50 cm. Hỏi mắt của họ có vấn đề gì không? Nếu có thì họ phải sử dụng loại kính gì để có thể cải thiện được khoảng nhìn thấy của mình?

Đáp án:

A bị cận thị => Đeo kính cận (TKPK)

B bị viễn thị => đeo kính lão (TKHT)

Bài 3: Biết tiêu cự của kính cận bằng khoảng cách từ mắt tới điểm cực viễn của mắt. Thấu kính nào trong số các thấu kính sau có thể dùng làm kính cận?

A. Thấu kính hội tụ có tiêu cự 20 cm.

B. Thấu kính phân kì có tiêu cự 20 cm.

C. Thấu kính hội tụ có tiêu cự 50 cm.

D. Thấu kính phân kì có tiêu cự 50 cm.

Đáp án: Chọn D

Bài 4: Sau khi đeo kính lão có tiêu cự 40 cm thì một người có thể nhìn được vật cách mắt tối thiểu 25 cm. Hỏi điểm cực cận của người đó nằm ở đâu?

Đáp án: C_c = d = 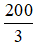(cm)

Bài 5: Tìm điểm cực viễn của mắt. Biết rằng khi đeo kính cận thì vật ở khoảng cách 400 cm thì sẽ được kính cho ảnh ở khoảng cách 0,8C_v.

Đáp án: C_v = f = 100 cm

Bài 6: Cho D là độ tụ của một thấu kính. D có đơn vị là điốp (dp). Với thấu kính phân kì, D được tính bởi công thức 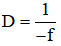(với f có đơn vị là m). Một người sử dụng kính cận có độ tụ -0,25dp. Hỏi điểm cực viễn của mắt người đó nằm ở đâu?

Đáp án: C_v = f = 4 m

Bài 7: Cho D là độ tụ của một thấu kính. D có đơn vị là điốp (dp). Với thấu kính phân kì, D được tính bởi công thức 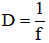. Với thấu kính phân kì, D được tính bởi công thức 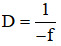(với f có đơn vị là m). Một người sử dụng kính đang nhìn một vật với độ tụ của mắt khi ấy là 52,5 dp. Hỏi vị trí thực của vật đó cách mắt bao nhiêu? Biết khoảng cách từ thể thủy tinh đến màng lưới là 2 cm; kính cận có độ tụ -0,5 dp.

Hướng dẫn:

- Tìm tiêu cự của mắt và kính.

- Tìm vị trí của ảnh tạo bởi kính mà mắt nhìn thấy.

- Tìm vị trí thực của vật.

Đáp án: d = 50 cm

Bài 8: Cho D là độ tụ của một thấu kính. D có đơn vị là điốp (dp). Với thấu kính hội tụ, D được tính bởi công thức 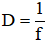(với f có đơn vị là m). Một người sử dụng kính lão có độ tụ 2,5dp để có thể nhìn được vật cách mắt tối thiểu 25 cm. Hỏi điểm cực cận của mắt người đó nằm ở đâu?

Đáp án: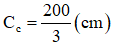

Bài 9: Cho D là độ tụ của một thấu kính. D có đơn vị là điốp (dp). Với thấu kính hội tụ, D được tính bởi công thức 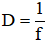(với f có đơn vị là m). Một người sử dụng kính đang nhìn một vật với độ tụ của mắt khi ấy là 51 dp. Hỏi vị trí thực của vật đó cách mắt bao nhiêu? Biết khoảng cách từ thể thủy tinh đến màng lưới là 2 cm; kính cận có độ tụ 2 dp.

Hướng dẫn:

- Tìm tiêu cự của mắt và kính.

- Tìm vị trí của ảnh tạo bởi kính mà mắt nhìn thấy.

- Tìm vị trí thực của vật.

Đáp án: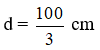

Bài 10: Tìm điểm cực cận của mắt. Biết rằng khi đeo kính lão thì vật ở khoảng cách 25 cm thì sẽ được kính cho ảnh ở khoảng cách 1,2f và ảnh trùng với cực cận của mắt.

Đáp án: C_c = 55 cm

Bài 11: Tìm điểm cực cận của mắt. Biết rằng khi đeo kính lão thì vật ở khoảng cách 30 cm thì sẽ nhìn được ảnh lớn gấp 10 lần vật, và khoảng cách tối thiểu để nhìn rõ vật khi đeo kính là 20 cm.

Hướng dẫn:

- Tìm tiêu cự của kính.

- Áp dụng công thức thấu kính hội tụ tạo ảnh ảo để tìm đáp án.

Đáp án: C_c = 50 cm

Bài 12: Một mắt có điểm cực viễn C_v = 2 m. Khi nhìn một tòa nhà qua kính cận thì ảnh của tòa nhà hiện trên màng lưới có chiều cao 0,8 cm. Tính chiều cao tòa nhà, biết khi đó kính cận cho ảnh cao bằng 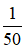chiều cao thực của tòa nhà và khoảng cách từ thể thủy tinh đến màng lưới là 2 cm.

Hướng dẫn:

- Đặt ẩn tỉ lệ giữa ảnh tạo bởi kính và ảnh hiện trên màng lưới.

=> Mối liên hệ giữa khoảng cách từ mắt đến ảnh và khoảng cách từ thể thủy tính đến màng lưới.

- Áp dụng công thức thấu kính cho kính cận để tìm đáp án.

Đáp án: h = 39,2 m.

Bài 13: Một mắt bị cận thị khi nhìn trực tiếp một vật cao 1m thì ảnh vật đó ở màng lưới cao 0,5 cm. Khi đeo kính cận rồi nhìn lại vật đó thì ảnh của vật đó ở màng lưới cao 0,1 cm. Tìm điểm cực viễn của mắt. Biết khoảng cách từ thể thủy tinh đến màng lưới là 2 cm.

Hướng dẫn:

- Tìm khoảng cách từ vật đến mắt.

- Tìm khoảng cách từ ảnh đến mắt.

- Áp dụng công thức thấu kính cho kính cận để tìm đáp án.

Đáp án: C_v = f = 1 m.