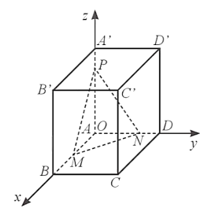
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2a, AD = 3a, AA' = 4a

❮ Bài trước Bài sau ❯

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2a, AD = 3a, AA' = 4a (a > 0). Gọi M, N, P lần lượt là các điểm thuộc các tia AB, AD, AA' sao cho AM = a, AN = 2a, AP = 3a. Tính khoảng cách từ điểm C' đến mặt phẳng (MNP).

Giải SBT Toán 12 Cánh diều Bài 1: Phương trình mặt phẳng

Bài 19 trang 48 SBT Toán 12 Tập 2: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2a, AD = 3a, AA' = 4a (a > 0). Gọi M, N, P lần lượt là các điểm thuộc các tia AB, AD, AA' sao cho AM = a, AN = 2a, AP = 3a. Tính khoảng cách từ điểm C' đến mặt phẳng (MNP).

Lời giải:

Xét hệ trục tọa độ Oxyz thỏa mãn A(0; 0; 0)(A trùng gốc tọa độ O), B(2a; 0; 0), D(0; 3a; 0), A'(0; 0; 4a).

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2a, AD = 3a, AA' = 4a

Ta có: M(a; 0; 0), N(0; 2a; 0), P(0; 0; 3a), C'(2a; 3a; 4a).

Phương trình mặt phẳng (MNP) là:

$\frac{x}{a} + \frac{y}{2 a} + \frac{z}{3 a} = 1$ $\Leftrightarrow \frac{x}{a} + \frac{y}{2 a} + \frac{z}{3 a} - 1 = 0$ .

Khoảng cách từ điểm C' đến mặt phẳng (MNP) là:

d(C', (MNP)) = $\frac{|\frac{2 a}{a} + \frac{3 a}{2 a} + \frac{4 a}{3 a} - 1|}{\sqrt{{(\frac{1}{a})}^{2} + {(\frac{1}{2 a})}^{2} + {(\frac{1}{3 a})}^{2}}} = \frac{23 a}{7} .$

Lời giải SBT Toán 12 Bài 1: Phương trình mặt phẳng hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯