Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.ABCD có đáy là hình chữ nhật

❮ Bài trước Bài sau ❯

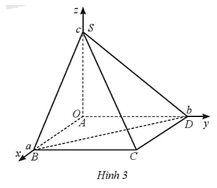
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.ABCD có đáy là hình chữ nhật và các điểm A(0; 0; 0), B(a; 0; 0), D(0; b; 0), S(0; 0; c) với a, b, c là các số dương (Hình 3).

Giải SBT Toán 12 Cánh diều Bài 1: Phương trình mặt phẳng

Bài 20 trang 48 SBT Toán 12 Tập 2: Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.ABCD có đáy là hình chữ nhật và các điểm A(0; 0; 0), B(a; 0; 0), D(0; b; 0), S(0; 0; c) với a, b, c là các số dương (Hình 3).

a) Tìm tọa độ của điểm C, trung điểm M của BC, trọng tâm G của tam giác SCD.

b) Lập phương trình mặt phẳng (SBD).

c) Tính khoảng cách từ điểm G đến mặt phẳng (SBD).

Lời giải:

a) Ta có $\vec{A B}$ = (a; 0; 0) và $\vec{D C} = \vec{A B}$ , suy ra $\vec{D C}$ = (a; 0; 0).

Mà D(0; b; 0) nên C(a; b; 0).

Trung điểm M của BC có tọa độ là: $(\frac{a + a}{2}; \frac{0 + b}{2}; \frac{0 + 0}{2})$ $= (a; \frac{b}{2}; 0)$ .

Có D(0; b; 0), S(0; 0; c), C(a; b; 0) nên tọa độ trọng tâm G(x; y; z) của tam giác SCD là: $\{\begin{cases} x = \frac{0 + 0 + a}{3} = \frac{a}{3} \\ y = \frac{b + 0 + b}{3} = \frac{2 b}{3} \\ c = \frac{0 + c + 0}{3} = \frac{c}{3} \end{cases}$

Vậy G $(\frac{a}{3}; \frac{2 b}{3}; \frac{c}{3}) .$

b) Ta có: D(0; b; 0), S(0; 0; c), B(a; 0; 0) nên phương trình mặt phẳng (SBD) là:

$\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$ $\Leftrightarrow \frac{x}{a} + \frac{y}{b} + \frac{z}{c} - 1 = 0$

c) Khoảng cách từ điểm G đến mặt phẳng (SBD) là:

$h = \frac{|\frac{\frac{a}{3}}{a} + \frac{\frac{2 b}{3}}{b} + \frac{\frac{c}{3}}{c} - 1|}{\sqrt{{(\frac{1}{a})}^{2} + {(\frac{1}{b})}^{2} + {(\frac{1}{c})}^{2}}}$ $= \frac{a b c}{3. \sqrt{a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2}}}$

Lời giải SBT Toán 12 Bài 1: Phương trình mặt phẳng hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯