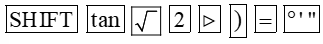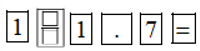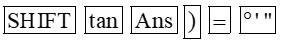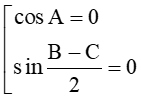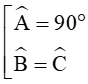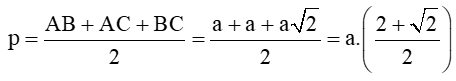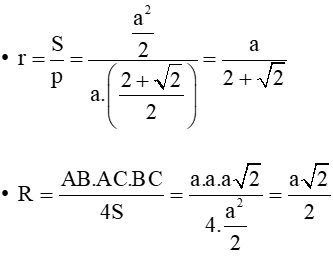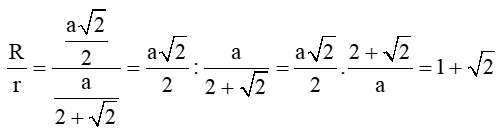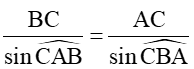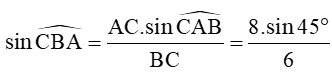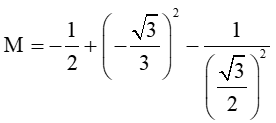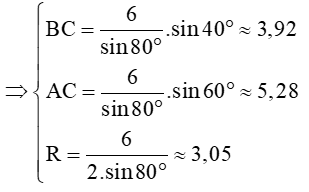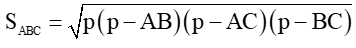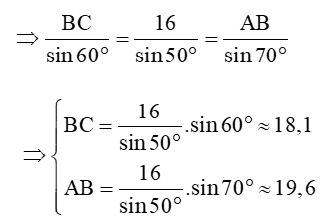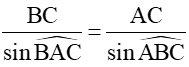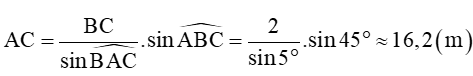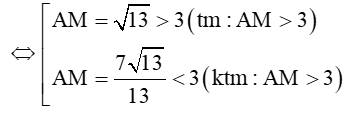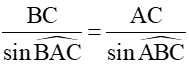Tổng hợp lý thuyết Toán 10 Chương 4 Chân trời sáng tạo
Với Tổng hợp lý thuyết Toán 10 Chương 4: Hệ thức lượng trong tam giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.
Tổng hợp lý thuyết Toán 10 Chương 4 Chân trời sáng tạo
Lý thuyết tổng hợp Toán 10 Chương 4
1. Giá trị lượng giác
Mở rộng khái niệm tỉ số lượng giác đối với góc nhọn cho những góc α bất kì với 0° ≤ α ≤ 180°, ta có định nghĩa sau đây:
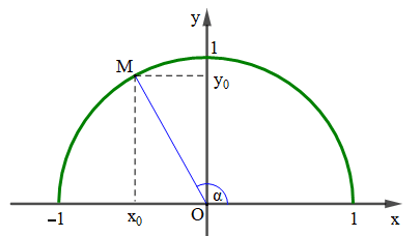
Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho 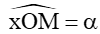
– Tung độ y0 của M là sin của góc α, kí hiệu là sinα = y0;
– Hoành độ x0 của M là côsin của góc α, kí hiệu là cosα = x0;
– Tỉ số (x0 ≠ 0) là tang của góc α, kí hiệu là tanα =
–Tỉ số (y0 ≠ 0) là côtang của góc α, kí hiệu là cotα =
Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.
Chú ý:
a) Nếu α là góc nhọn thì các giá trị lượng giác của α đều dương.
Nếu α là góc tù thì sinα > 0, cosα < 0, tanα < 0, cotα < 0.
b) tanα chỉ xác định khi α ≠ 90°.
cotα chỉ xác định khi α ≠ 0° và α ≠ 180°.
2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
– Từ lớp dưới ta đã biết hai góc phụ nhau thì các tỉ số lượng giác của chúng có mối liên hệ:
sin(90° – α) = cosα;
cos(90° – α) = sinα;
tan(90° – α) = cotα;
cot(90° – α) = tanα.
– Mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau
Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có:
sin(180° ‒ α) = sinα;
cos(180° ‒ α) = ‒cosα;
tan(180° ‒ α) = ‒tanα (α ≠ 90°);
cot(180° ‒ α) = ‒cotα (0° < α < 180°).
3. Giá trị lượng giác của một số góc đặc biệt
Dưới đây là bảng giá trị lượng giác của một số góc đặc biệt:

Chú ý: Trong bảng, kí hiệu “||” để chỉ giá trị lượng giác không xác định.
4. Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc
Có nhiều loại máy tính cầm tay có thể giúp tính nhanh chóng giá trị lượng giác của một góc.
Chẳng hạn, ta có thể thực hiện trên máy tính cầm tay vinacal 680EX PLUS như sau:
Sau khi mở máy, ẩn liên tiếp các phím 
Ấn phím 
Ấn tiếp phím 
Ấn các phím 
4.1. Tính các giá trị lượng giác của góc
Ví dụ. Sử dụng máy tính cầm tay, tính sin125°, cos50°12', tan160°56'25'', cot100°.
Hướng dẫn giải
– Để tính sin125°, ta bấm liên tiếp các phím sau đây: 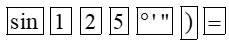
Khi đó ta được kết quả hiện trên màn hình là:
Vậy sin125° ≈ 0,8191520443.
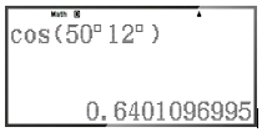
– Để tính cos50°12', ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy cos50°12' ≈ 0,6401096995.
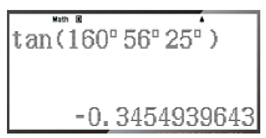
– Để tính tan160°56'25'', ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy tan160°56'25'' ≈ ‒0,34549339643.
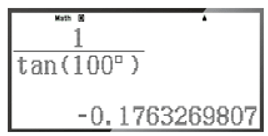
– Để tính cot100°, ta bấm liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy cot100° ≈ ‒0,1763269807.
4.2. Xác định số đo của góc khi biết giá trị lượng giác của góc đó
Ví dụ. Sử dụng máy tính cầm tay, tìm α (0° < α < 180°) biết sinα = 0,51; cosα = ‒0,7; tanα = ; cotα = 1,7.
Hướng dẫn giải
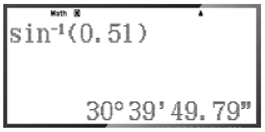
– Để tìm α khi biết sinα = 0,51, ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy với sinα = 0,51 thì α ≈ 30°39'50''.
Ta đã được học với 0° < α < 180° thì sin(180° ‒ α) = sinα nên ngoài giá trị α ≈ 30°39'50'' thì ta còn có giá trị α ≈ 180° ‒ 30°39'50'' ≈ 149°20'10''.
Ta bấm máy tính như sau:
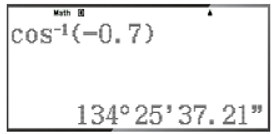
– Để tìm α khi biết cosα = ‒0,7, ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy với cosα = ‒0,7 thì α ≈ 134°25'37''.
– Để tìm α khi biết tanα = ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy với tanα = thì α ≈ 54°44'8''.
– Để tìm α khi biết cotα = 1,7, trước hết ta tính tanα = , ta ấn liên tiếp các phím sau đây:
Khi đó ta được kết quả hiện trên màn hình là:
Sau đó ta bấm liên tiếp các phím:
Khi đó ta được kết quả hiện trên màn hình là:
Vậy với cotα = 1,7 thì α ≈ 30°27'56''.
5. Định lí côsin trong tam giác
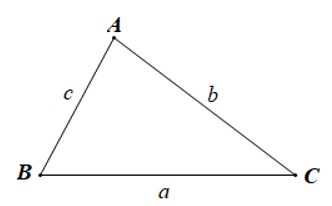
Định lí côsin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
a2 = b2 + c2 – 2bc.cosA;
b2 = c2 + a2 – 2ca.cosB;
c2 = a2 + b2 – 2ab.cosC.
Từ định lí côsin, ta có hệ quả sau đây:
Hệ quả:
cosA =
cosB =
6. Định lí sin trong tam giác
Định lí sin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
= 2R,
trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.
Từ định lí sin, ta có hệ quả sau đây:
Hệ quả:
a = 2R.sinA; b = 2R.sinB; c = 2R.sinC;
sinA = ; sinB = ; sinC = .
7. Các công thức tính diện tích tam giác
Cho tam giác ABC. Ta kí hiệu:
+) BC = a, CA = b, AB = c.
+) ha, hb, hc là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB.
+) R là bán kính đường tròn ngoại tiếp tam giác.
+) r là bán kính đường tròn nội tiếp tam giác.
+) p là nửa chu vi tam giác.
+) S là diện tích tam giác.
Ta có các công thức tính diện tích tam giác sau:
(1) S = aha = bhb = chc;
(2) S = ab.sinC = bc.sinA = ac.sinB;
(3) S = ;
(4) S = pr;
(5) (Công thức Heron).
8. Giải tam giác
Giải tam giác là tìm số đo các cạnh và các góc còn lại của tam giác khi ta biết được các yếu tố đủ để xác định tam giác đó.
Để giải tam giác, ta thường sử dụng một cách hợp lí các hệ thức lượng như: định lí sin, định lí côsin và các công thức tính diện tích tam giác.
9. Áp dụng giải tam giác vào thực tế
Vận dụng giải tam giác giúp ta giải quyết rất nhiều bài toán trong thực tế, đặc biệt là trong thiết kế và xây dựng.
Bài tập tổng hợp Toán 10 Chương 4
1. Bài tập trắc nghiệm
Câu 1. Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:
A. ‒1;
B. 0;
C. 1;
D. 2.
Hướng dẫn giải
Đáp án đúng là: B
Xét tam giác ABC ta có: 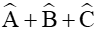
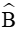
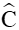
cos(B + C) = cos(180° ‒ A) = ‒cosA;
Và sin(B + C) = sin(180° ‒ A) = sinA.
Do đó:
sinA.cos(B + C) + cosA.sin(B + C)
= sinA.(‒cosA) + cosA.sinA
= ‒sinA.cosA + cosA.sinA
= 0
Vậy sinA.cos(B + C) + cosA.sin(B + C) = 0.
Câu 2. Cho góc α (0° ≤ α ≤ 180°) với tanα = ‒3. Giá trị của là
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: D
Vì tanα = ‒3 nên = -3 do đó cosα ≠ 0
Ta có:
(do cosα ≠ 0)
Vậy
Câu 3. Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 180°, giá trị của biểu thức: M = cosα.cosβ – sinβ.sinα là:
A. M = ‒1;
B. M = 2;
C. M = 0;
D. M = 1.
Hướng dẫn giải
Đáp án đúng là: A
Vì hai góc α và β (0° ≤ α, β ≤ 180°) là hai góc bù nhau (do α + β = 180°) nên:
cosβ = ‒cosα và sinβ = sinα.
Ta có: M = cosα.cosβ – sinβ.sinα
M = cosα.(‒cosα) ‒ sinα.sinα = ‒cos2α ‒ sin2α
M = ‒(cos2α + sin2α)
Mà cos2α + sin2α = 1 (đã được chứng minh ở bài 5, trang 65, Sách giáo khoa Toán 10, Tập một).
Vậy M = ‒1.
Câu 4. Cho tam giác ABC (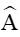
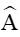
A. 105°;
B. 120°;
C. 135°;
D. 150°.
Hướng dẫn giải
Đáp án đúng là: A
Trong tam giác ABC có 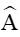
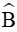
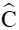
Áp dụng định lí sin trong tam giác ABC ta có:
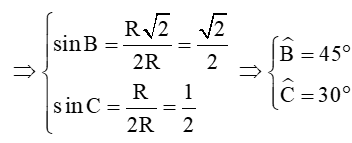
Xét tam giác ABC có 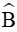
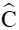
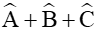
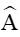
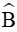
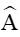
Vậy 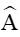
Câu 5. Một tam giác có độ dài ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: B
Góc nhỏ nhất ứng với cạnh đối diện có độ dài nhỏ nhất.
Giả sử tam giác ABC có AB = 2, AC = 3, BC = 4. Khi đó góc nhỏ nhất là góc C ứng với cạnh đối diện AB.
Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
cosC =
Vậy côsin của góc nhỏ nhất trong tam giác bằng
Câu 6. Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
A. 2S;
B. 3S;
C. 4S;
D. 6S.
Hướng dẫn giải
Đáp án đúng là: D
Ta có diện tích ban đầu của tam giác ABC là: S = .BC.AC.sinC.
Diện tích của tam giác mới sau khi thay đổi kích thước là:
S' = .2BC.3AC.sinC = 6= 6S.
Vậy diện tích của tam giác mới được tạo thành là 6S.
Câu 7. Tam giác ABC có góc A nhọn, AB = 5, AC = 8, diện tích bằng 12. Độ dài cạnh BC là khoảng:
A. 2
B. 3
C. 4;
D. 5.
Hướng dẫn giải
Đáp án đúng là: D
Diện tích tam giác ABC là: S = .AB.Ac.sinA sinA =
sinA = 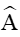
Xét tam giác ABC có AB = 5, AC = 8 và 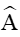
BC2 = AB2 + AC2 – 2.AB.AC.cosA
BC2 ≈ 52 + 82 – 2.5.8.cos36°52' ≈ 25
BC ≈ 5.
Vậy BC ≈ 5.
Câu 8. Cho tam giác ABC. Biết AB = 2, BC = 3 và 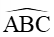
A. 5+ và ;
B. 5+ và ;
C. 5+ và ;
D. 5+ và .
Hướng dẫn giải
Đáp án đúng là: B
Xét tam giác ABC có AB = 2, BC = 3 và 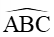
AC2 = AB2 + BC2 – 2.AB.BC.cos
AC2 = 22 + 32 – 2.2.3.cos60° = 7
AC =
Do đó chu vi tam giác ABC là:
AB + AC + BC = 2 +3 + = 5 +
Diện tích tam giác ABC là:
S = .BA.BC.sin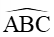
Vậy chu vi và diện tích tam giác ABC lần lượt là: 5 + và
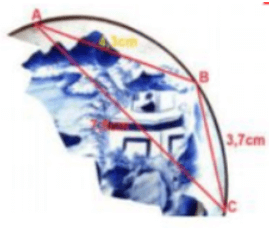
Câu 9. Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3 cm; BC = 3,7 cm; CA = 7,5 cm).
Bán kính của chiếc đĩa này bằng (kết quả làm tròn đến chữ số thập phân thứ hai):
A. 5,73 cm;
B. 6,01 cm;
C. 5,85 cm;
D. 4,57 cm.
Hướng dẫn giải
Đáp án đúng là: A
Bán kính R của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC.
Nửa chu vi của tam giác ABC là:
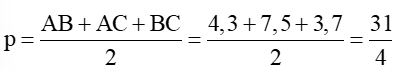
Diện tích tam giác ABC theo công thức Heron là:
Mặt khác:
Vậy bán kính của chiếc đĩa là khoảng 5,73 cm.
Câu 10. Cho tam giác ABC thỏa mãn: . Khi đó ABC là một tam giác:
A. Tam giác vuông;
B. Tam giác cân;
C. Tam giác vuông hoặc cân;
D. Tam giác đều.
Hướng dẫn giải
Đáp án đúng là: C
Ta có: cosA.sin = 0
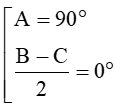
DABC vuông tại A hoặc DABC cân tại A.
Vậy DABC vuông tại A hoặc DABC cân tại A.
2. Bài tập tự luận
Bài 1. Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tính tỉ số .
Hướng dẫn giải
Giả sử AB = AC = a.
Xét tam giác ABC vuông cân tại A, theo định lí Pythagore ta có:
BC2 = AB2 + AC2 = a2 + a2 = 2a2
BC = a
Do đó nửa chu vi tam giác ABC là:
Tam giác ABC vuông tại A nên diện tích tam giác ABC là:
S = .AB.AC = .a.a = (đơn vị diện tích).
Mặt khác S = pr =
Suy ra:
Do đó
Vậy
Bài 2. Nhà thầu đất Đức đã được cung cấp các kích thước sau đây qua điện thoại từ khách hàng: Khu vườn hình tam giác ABC có 
a) Giải thích tại sao nhà thầu đất Đức cần thêm thông tin từ khách hàng của mình.
b) Cần khối lượng đất tối đa là bao nhiêu (để tạo thành nền của khu đất) nếu khách hàng của anh Đức không thể cung cấp thêm thông tin cần thiết?
Hướng dẫn giải
a) Áp dụng định lí sin với tam giác ABC ta có:
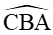
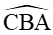
Như vậy ta có thể có hai gá trị khác nhau của góc CBA nên hình tam giác không được xác định một cách duy nhất.
Điều đó giải thích tại sao anh Đức cần thêm thông tin về khu vườn.
b) Nền đất của khu vườn là một khối lăng trụ đứng với đáy là tam giác ABC và chiều cao không đổi là 10 cm, nên khối lượng đất tối đa để tạo ra nền của khu đất tỉ lệ với diện tích lớn nhất của tam giác ABC.
+) Nếu 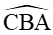

Khi đó diện tích của tam giác ABC là:
S = .CA.CB.sin
+) Nếu 

Khi đó diện tích của tam giác ABC là:
S = .CA.CB.sin
Khi đó diện tích lớn nhất của tam giác ABC là 21,65 m2.
Đổi 10 cm = 0,1 m.
Khối lượng đất tối đa cần khoảng: 21,65. 0,1 ≈ 2,165 (m3)
Vậy khối lượng đất tối đa cần để tạo thành nền của khu đất khoảng 2,165 m3.
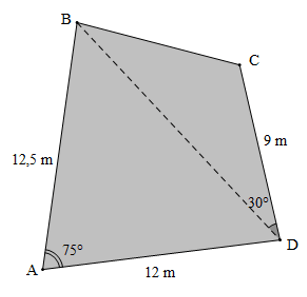
Bài 3. Vợ chồng anh Minh đang xem xét mua một mảnh đất. Nhân viên nhà đất cung cấp cho họ một bản vẽ chi tiết như hình vẽ dưới. Tính diện tích của mảnh đất và số tỉ đồng vợ chồng anh Minh cần dùng để mua đất biết giá đất là 25 triệu đồng/ m2 đất (làm tròn kết quả đến chữ số thập phân thứ hai).
Hướng dẫn giải
Diện tích của mảnh đất là tổng diện tích của hai tam giác ABD và tam giác BCD.
Ta có: SABD = .AB.AD.sin
Áp dụng định lí côsin cho tam giác BAD ta có:
BD2 = AB2 + AD2 – 2.AB.AD.cos
BD2 = 12,52 + 122 ‒ 2.12,5.12.cos75°
BD ≈ 14,92 (m)
Do đó SBCD = .BD.CD.sin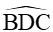
Khi đó diện tích mảnh đất là:
S = SABD + SBCD ≈ 72,44 + 33,57 = 106,01 (m2)
Số tiền vợ chồng anh Minh cần dùng để mua mảnh đất này là:
106,01 . 25 = 2 650,25 (triệu đồng) = 2,65025 tỉ đồng ≈ 2,65 tỉ đồng.
Vậy diện tích mảnh đất khoảng 106,01 m2 và số tiền cần dùng mua đất là khoảng 2,65 tỉ đồng.
Bài 4. Tính giá trị biểu thức:
a) A = sin30°.cos45°.sin60° ‒ cos120°.tan135°.cot150°.
b) B = cos0° + cos20° + cos40° + … + cos160° + cos180°;
c) C = sin(180o-x) - cos(90o-x) + sin2x. - tan2x
Hướng dẫn giải
a) A = sin30°.cos45°.sin60° ‒ cos120°.tan135°.cot150°
b) B = cos0° + cos20° + cos40° + … + cos160° + cos180°
B = (cos0° + cos180°) + (cos20° + cos160°) + … + (cos80° + cos100°)
B = (cos0° ‒ cos0°) + (cos20° ‒ cos20°) + … + (cos80° ‒ cos80°) (hai góc bù nhau)
B = 0.
c) C = sin(180o-x) - cos(90o-x) + sin2x. - tan2x
C = sinx - sinx + sin2x. - tan2x
C = 0 + tan2x ‒ tan2x
C = 0.
Bài 5. Cho góc α (0° ≤ α ≤ 180°) với tanα = -. Tính giá trị biểu thức:
M = cosα + cot2α -
Hướng dẫn giải
Với tanα = - ta có α = 120°.
Suy ra: sinα = ; cosα = -; cotα = -
Do đó:
M = cosα + cot2α -
Vậy
Bài 6. Tính độ dài cạnh và góc chưa biết của tam giác ABC, diện tích tam giác ABC, bán kính đường tròn ngoại tiếp, bán kính đường tròn nội tiếp và đường cao kẻ từ C của tam giác ABC (làm tròn kết quả đến chữ số thập phân thứ hai) trong hình sau:
Hướng dẫn giải
Xét tam giác ABC có 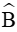
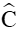
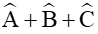
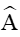
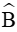
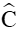
Theo định lí sin ta có:
Nửa chu vi tam giác ABC là:
Áp dụng công thức Heron ta có diện tích tam giác ABC là:
(đơn vị diện tích)
Mặt khác SABC = pr
Lại có SABC = .AB.hc (với hC là đường cao kẻ từ C đến AB của tam giác ABC)
Vậy 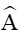
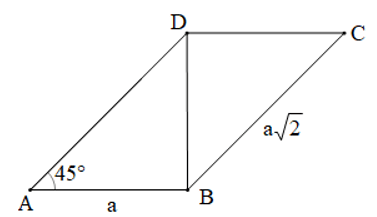
Bài 7. Cho hình bình hành ABCD có AB = a, BC = a và 
Hướng dẫn giải
Vì ABCD là hình bình hành nên AD = BC (tính chất hình bình hành)
Mà BC = a nên AD = a
Diện tích tam giác ABD là:
SABD = .BD.CD.sin
Do đó diện tích hình bình hành ABCD là:
SABCD = 2.SABD = 2. = a2 (đơn vị diện tích).
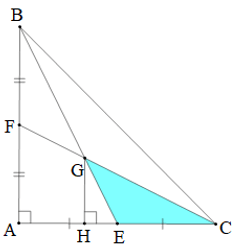
Bài 8. Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và CF cắt nhau tại G. Tính diện tích tam giác GEC.
Hướng dẫn giải
Vì BE là trung tuyến của tam giác ABC nên E là trung điểm của AC.
Do đó EC = .AC = .30 = 15 (cm)
Hai đường trung tuyến BE và CF cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Khi đó GE = BE (tính chất trọng tâm của tam giác)
Gọi H là chân đường vuông góc kẻ từ G xuống AC.
Suy ra GH // AB.
Do đó (định lí Thalès trong tam giác ABE)
Hay GH = .30 = 10 (cm)
Diện tích tam giác GEC là:
SGEC = .GH.EC = .10.15 = 75 (cm2)
Vậy diện tích tam giác GEC là 75 cm2.
Bài 9. Giải tam giác ABC biết AC = 16, 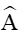
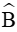
Hướng dẫn giải
Xét tam giác ABC có 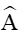
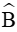
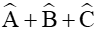
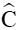
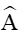
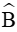
Theo định lí sin ta có:
Vậy 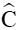
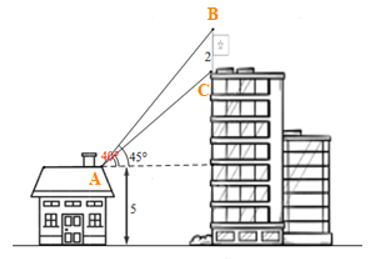
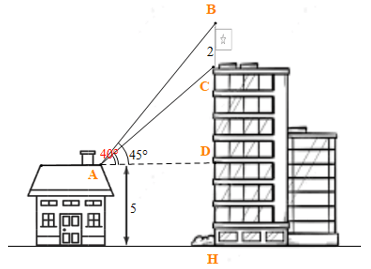
Bài 10. Trên nóc một toà nhà có một cột cờ cao 2 m. Từ vị trí quan sát A cao 5 m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột cờ dưới góc 45° và 40° so với phương nằm ngang (hình vẽ). Tìm chiều cao của toà nhà.
Hướng dẫn giải
Từ hình vẽ ta có 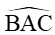
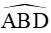
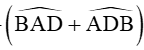
Do đó 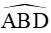
Suy ra: 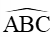
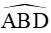
Áp dụng định lí sin trong tam giác ABC có:
Suy ra
Trong tam giác vuông ADC có:
CD = AC.sin
Do đó CH = CD + DH ≈ 10,4 + 5 ≈ 15,4 (m).
Vậy chiều cao của toà nhà là khoảng 15,4 m.
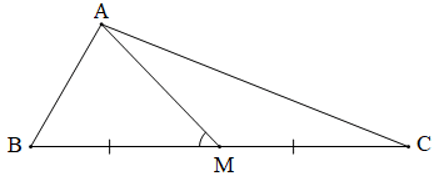
Bài 11. Tam giác ABC có AB = 3, BC = 8, M là trung điểm của BC, cos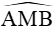
Hướng dẫn giải
Vì M là trung điểm của BC nên BM = MC = BC = .8=4.
Xét tam giác ABM, áp dụng hệ quả định lí côsin ta có:
cos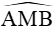
Do đó AM = .
Vì 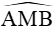
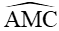
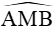
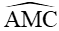
Suy ra cos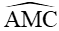
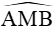
Xét tam giác AMC, áp dụng định lí côsin ta có:
- 2.AM.CM.cos
AC2 = ()2 + 42 - 2..4.
AC2 = 49
AC = 7.
Xét tam giác ABM có AB = 3, BM = 4, AM = áp dụng định lí côsin ta có:
cos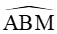
cos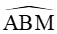
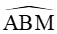
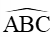
Xét tam giác ABC, áp dụng định lí sin ta có:
Mà tam giác ABC là tam giác tù nên 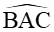
Xét tam giác ABC ta có:
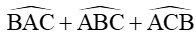

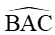

Vậy AM = , AC = 7, 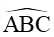

Học tốt Toán 10 Chương 4
Các bài học để học tốt Chương 4 Toán lớp 10 hay khác: