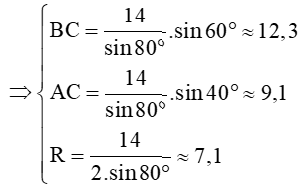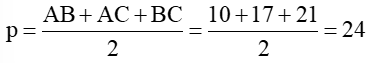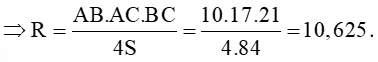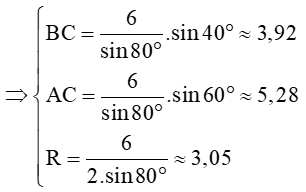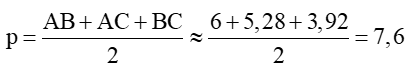Định lí côsin và định lí sin (Lý thuyết Toán lớp 10) - Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 10 Bài 2: Định lí côsin và định lí sin sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Định lí côsin và định lí sin (Lý thuyết Toán lớp 10) - Chân trời sáng tạo

Lý thuyết Định lí côsin và định lí sin

1. Định lí côsin trong tam giác

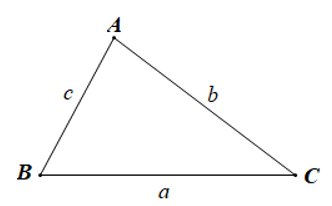
Định lí côsin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:

a² = b² + c² – 2bc.cosA;

b² = c² + a² – 2ca.cosB;

c² = a² + b² – 2ab.cosC.

Từ định lí côsin, ta có hệ quả sau đây:

Hệ quả:

cosA = $\frac{b^2+c^2-a^2}{2bc};$

cosB = $\frac{c^2+a^2-b^2}{2ca};$

cosC = $\frac{a^2+b^2-c^2}{2ab}.$

Ví dụ 1. Cho tam giác ABC có AB = 4, AC = 5 và cosA = $\frac{3}{5}$. Tính độ dài cạnh BC, số đo góc B và C (làm tròn số đo góc đến độ).

Hướng dẫn giải

Xét tam giác ABC có AB = 4, AC = 5 và cosA = $\frac{3}{5}$ áp dụng định lí côsin ta có:

BC² = AB² + AC² – 2.AB.AC.cosA

$\Rightarrow$BC²=4² + 5² - 2.4.5.$\frac{3}{5}$

$\Rightarrow$ BC² = 17

$\Rightarrow$BC = $\sqrt{17}$

Áp dụng hệ quả định lí côsin ta có:

+) cos B = $\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}$

$\Rightarrow \cos B=\frac{4^2+17-5^2}{\mathrm{2.4.}\sqrt{17}}$

$\Rightarrow \cos B=\frac{\sqrt{17}}{17}\Rightarrow B\approx 76°.$

+) cosC = $\frac{A{C}^2+B{C}^2-A{B}^2}{2.AC.BC}$

$\Rightarrow \cos C=\frac{5^2+17-4^2}{\mathrm{2.5.}\sqrt{17}}$

$\Rightarrow \cos C=\frac{13\sqrt{17}}{85}\Rightarrow C\approx 51°.$

Vậy BC = $\sqrt{17}$, B ≈ 76° và C ≈ 51°.

2. Định lí sin trong tam giác

Định lí sin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$= 2R,

trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.

Từ định lí sin, ta có hệ quả sau đây:

Hệ quả:

a = 2R.sinA; b = 2R.sinB; c = 2R.sinC;

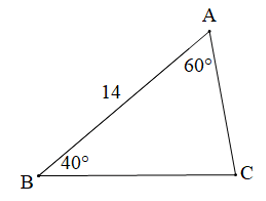
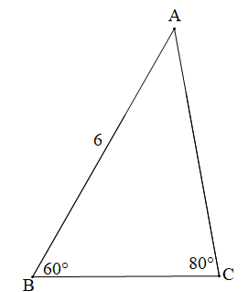
Ví dụ 2. Cho hình vẽ:

Tính các cạnh, các góc chưa biết và bán kính đường tròn ngoại tiếp R của tam giác ABC (làm tròn độ dài đến chữ số thập phân thứ nhất).

Hướng dẫn giải

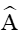
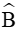
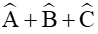
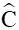
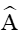
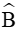
Xét tam giác ABC có = 60^o, = 40^o ta có:

= 180^o (định lí tổng ba góc trong tam giác)

$\Rightarrow$ = 180^o- - = 180^o - 60^o - 40^o = 80^o

Theo định lí sin ta có: $\frac{BC}{\sin A}=\frac{AC}{\sin B}=\frac{AB}{\sin C}$ = 2R

$\Rightarrow \frac{BC}{\sin 60°}=\frac{AC}{\sin 40°}=\frac{14}{\sin 80°}=2R$

Vậy = 80^o; BC ≈ 12,3; AC ≈ 9,1 và R ≈ 7,1.

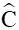
3. Các công thức tính diện tích tam giác

Cho tam giác ABC. Ta kí hiệu:

+) BC = a, CA = b, AB = c.

+) h_a, h_b, h_c là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB.

+) R là bán kính đường tròn ngoại tiếp tam giác.

+) r là bán kính đường tròn nội tiếp tam giác.

+) p là nửa chu vi tam giác.

+) S là diện tích tam giác.

Ta có các công thức tính diện tích tam giác sau:

(1) S = $\frac{1}{2}$ah_a = $\frac{1}{2}$bh_b = $\frac{1}{2}$ch_c

(2) S = $\frac{1}{2}$ab.sinC = $\frac{1}{2}$bc.sinA = $\frac{1}{2}$ac.sinB;

(3) S = $\frac{abc}{4R}$;

(4) S = pr;

(5) $S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$ (Công thức Heron).

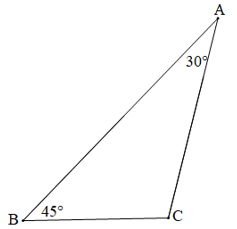
Ví dụ 3. Tính diện tích S của tam giác ABC, bán kính đường tròn nội tiếp r và bán kính đường tròn ngoại tiếp R (nếu chưa biết) (làm tròn kết quả đến chữ số thập phân thứ ba) trong các trường hợp sau:

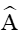
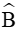
a) = 30^o, = 45^o , R = 3;

b) AB = 10, AC = 17, BC = 21.

Hướng dẫn giải

a)

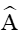
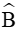
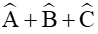
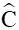
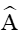
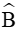
Xét tam giác ABC có = 30^o, = 45^o ta có:

= 180^o (định lí tổng ba góc trong tam giác)

$\Rightarrow$ = 180^o- - = 180^o - 30^o - 45^o = 105^o

Theo hệ quả định lí sin ta có:

+) BC = 2R.sinA = 2.3.sin30° = 6.$\frac{1}{2}$ = 3;

+) AC = 2R.sinB = 2.3.sin45° = $6.\frac{\sqrt{2}}{2}=3\sqrt{2};$

+) AB = 2R.sinC = 2.3.sin105° = $6.\frac{\sqrt{6}+\sqrt{2}}{4}=\frac{3\left(\sqrt{6}+\sqrt{2}\right)}{2}.$

Theo công thức tính diện tích tam giác ta có:

S_ABC = $\frac{1}{2}$.AB.AC.sinA = $\frac{1}{2}$.$\frac{3.\left(\sqrt{6}+\sqrt{2}\right)}{2}.3\sqrt{2}$.sin30^o $\approx$6,147 (đơn vị diện tích)

Ta có nửa chu vi tam giác ABC là:

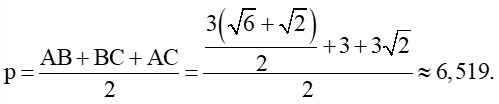
Mà S_ABC = pr $\Rightarrow r=\frac{S_{ABC}}{p}\approx \frac{6,147}{6,519}\approx 0,943.$

Vậy S_ABC ≈ 6,147 (đơn vị diện tích) và r ≈ 0,943.

b) Nửa chu vi tam giác ABC là:

Áp dụng công thức Heron ta có:

$S_{ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}$

$S_{ABC}=\sqrt{24.\left(24-10\right).\left(24-17\right).\left(24-21\right)}=84$ (đơn vị diện tích)

Mà S_ABC = pr $\Rightarrow r=\frac{S_{ABC}}{p}=\frac{84}{24}=3,5$

Lại có $S_{ABC}=\frac{AB.AC.BC}{4R}$

Vậy S = 84 (đơn vị diện tích) và r = 3,5; R = 10,625.

Bài tập Định lí côsin và định lí sin

1. Bài tập trắc nghiệm

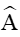
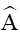
Câu 1. Cho tam giác ABC ( là góc tù) nội tiếp đường tròn bán kính R, AB = R, AC = R$\sqrt{2}$ Số đo của bằng

A. 105°;

B. 120°;

C. 135°;

D. 150°.

Hướng dẫn giải

Đáp án đúng là: A

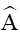
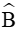
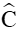
Trong tam giác ABC có là góc tù nên , là góc nhọn.

Áp dụng định lí sin trong tam giác ABC ta có: $\frac{AC}{\sin B}=\frac{AB}{\sin C}=2R$

$\frac{AC}{\sin B}=\frac{AB}{\sin C}=2R$

(vì là góc nhọn)

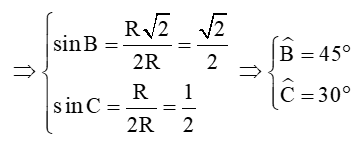
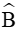
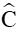
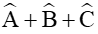
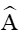
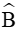
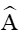
Xét tam giác ABC có = 45^o , = 30^o ta có:

= 180^o (định lí tổng ba góc trong tam giác)

$\Rightarrow$= 180^o - -

$\Rightarrow$= 180^o - 45^o - 35^o = 105^o

Vậy 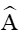= 105^o

Câu 2. Một tam giác có độ dài ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?

A. $\frac{\sqrt{15}}{8};$

B. $\frac{7}{8};$

C. $\frac{1}{2};$

D. $\frac{\sqrt{14}}{8}.$

Hướng dẫn giải

Đáp án đúng là: B

Góc nhỏ nhất ứng với cạnh đối diện có độ dài nhỏ nhất.

Giả sử tam giác ABC có AB = 2, AC = 3, BC = 4. Khi đó góc nhỏ nhất là góc C ứng với cạnh đối diện AB.

Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:

cosC = $\frac{A{C}^2+B{C}^2-A{B}^2}{2.AC.BC}=\frac{3^2+4^2-2^2}{\mathrm{2.3.4}}=\frac{7}{8}.$

Vậy côsin của góc nhỏ nhất trong tam giác bằng $\frac{7}{8}.$

Câu 3. Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:

A. 2S;

B. 3S;

C. 4S;

D. 6S.

Hướng dẫn giải

Đáp án đúng là: D

Ta có diện tích ban đầu của tam giác ABC là: S = $\frac{1}{2}$.BC.AC.sinC.

Diện tích của tam giác mới sau khi thay đổi kích thước là:

S' = $\frac{1}{2}$.2BC.3AC.sinC = 6$\left(\frac{1}{2}.BC.AC.\sin C\right)$= 6S.

Vậy diện tích của tam giác mới được tạo thành là 6S.

2. Bài tập tự luận

Bài 1. Tính độ dài cạnh và góc chưa biết của tam giác ABC, diện tích tam giác ABC, bán kính đường tròn ngoại tiếp, bán kính đường tròn nội tiếp và đường cao kẻ từ C của tam giác ABC (làm tròn kết quả đến chữ số thập phân thứ hai) trong hình sau:

Hướng dẫn giải

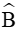
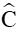
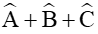
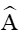
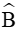
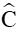
Xét tam giác ABC có = 60^o , = 80^o ta có:

= 180^o (định lí tổng ba góc trong tam giác)

$\Rightarrow$= 180^o - - = 180^o - 60^o - 80^o = 40^o

Theo định lí sin ta có: $\frac{BC}{\sin A}=\frac{AC}{\sin B}=\frac{AB}{\sin C}=2R$

$\Rightarrow \frac{BC}{\sin 40°}=\frac{AC}{\sin 60°}=\frac{6}{\sin 80°}=2R$

Nửa chu vi tam giác ABC là:

Áp dụng công thức Heron ta có diện tích tam giác ABC là:

$S_{ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}$

$S_{ABC}\approx \sqrt{7,6.\left(7,6-6\right).\left(7,6-5,28\right).\left(7,6-3,92\right)}\approx 10,19$ (đơn vị diện tích)

Mặt khác S_ABC = pr $\Rightarrow r=\frac{S_{ABC}}{p}\approx \frac{10,19}{7,6}\approx 1,34$

Lại có $S_{ABC}=\frac{1}{2}.AB.h_C$ (với h_C là đường cao kẻ từ C đến AB của tam giác ABC)

$\Rightarrow h_C=\frac{2.S_{ABC}}{AB}\approx \frac{2.10,19}{6}\approx 3,4.$

Vậy = 40^o; BC ≈ 3,92; AC ≈ 5,28; R ≈ 3,05; r ≈ 1,34; h_C ≈ 3,4 và S ≈ 10,19 (đơn vị diện tích).

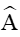
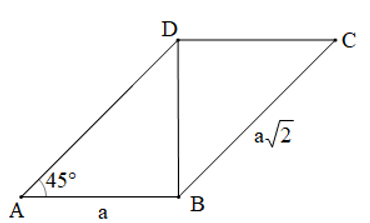
Bài 2. Cho hình bình hành ABCD có AB = a, BC = a$\sqrt{2}$ và = 45^o. Tính diện tích hình bình hành đó.

Hướng dẫn giải

Vì ABCD là hình bình hành nên AD = BC (tính chất hình bình hành)

Mà BC = a$\sqrt{2}$ nên AD = a$\sqrt{2}$

Diện tích tam giác ABD là:

(đơn vị diện tích)

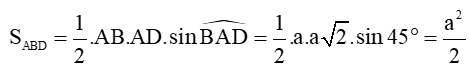
Do đó diện tích hình bình hành ABCD là:

$S_{ABCD}=2S_{ABD}=2.\frac{a^2}{2}=a^2$ (đơn vị diện tích).

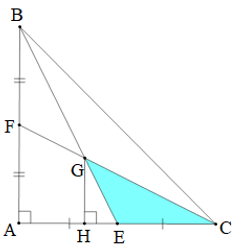
Bài 3. Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và CF cắt nhau tại G. Tính diện tích tam giác GEC.

Hướng dẫn giải

Vì BE là trung tuyến của tam giác ABC nên E là trung điểm của AC.

Do đó EC = $\frac{1}{2}$.AC = $\frac{1}{2}$.30 = 15 (cm)

Hai đường trung tuyến BE và CF cắt nhau tại G nên G là trọng tâm của tam giác ABC.

Khi đó GE = $\frac{1}{3}$BE (tính chất trọng tâm của tam giác)

Gọi H là chân đường vuông góc kẻ từ G xuống AC.

Suy ra GH // AB.

Do đó $\frac{GH}{BA}=\frac{GE}{BE}$ (định lí Thalès trong tam giác ABE)

Hay $\frac{GH}{BA}=\frac{1}{3}\Rightarrow$GH = $\frac{1}{3}$.30 = 10 (cm)

Diện tích tam giác GEC là:

S_GEC = $\frac{1}{2}$.GH.EC = $\frac{1}{2}$.10.15 = 75 (cm²)

Vậy diện tích tam giác GEC là 75 cm².

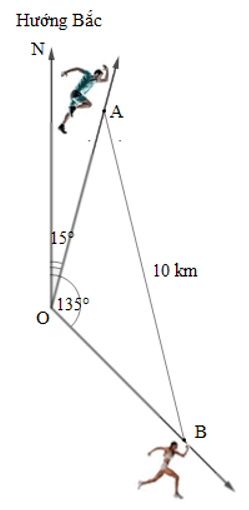
Bài 4. Vào lúc 9 giờ sáng, hai vận động viên A và B xuất phát từ cùng một vị trí O. Vận động viên A chạy với vận tốc 13 km/h theo một góc so với hướng Bắc là 15°, vận động viên B chạy với vận tốc 12 km/h theo một góc so với hướng Bắc là 135° (hình vẽ).

Tại thời điểm nào thì vận động viên A cách vận động viên B một khoảng 10 km (làm tròn kết quả đến phút)?

Hướng dẫn giải

Gọi x giờ (x > 0) là khoảng thời gian kể từ khi bắt đầu chạy từ điểm O đến khi hai vận động viên cách nhau 10 km.

Khi đó đoạn đường mà vận động viên A chạy được là 13x (km);

Đoạn đường mà vận động viên B chạy được là 12x (km).

Theo hình vẽ trên ta có: AB = 10, OA = 13x, OB = 12x và 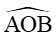= 135^o - 15^o = 120^o.

Áp dụng định lí côsin trong tam giác OAB ta có:

AB² = OA² + OB² – 2.OA.OB. sin

$\Rightarrow$ 10² = (13x)² + (12x)² – 2.13x.12x.sin120°

$\Rightarrow$ 10² = 169x² + 144x² – 312x².$\frac{\sqrt{3}}{2}$

$\Rightarrow$10² = (313 - 156$\sqrt{3}$)x²

$\Rightarrow$ x² = $\frac{10}{313-156\sqrt{3}}$

$\Rightarrow$ x ≈ 0,483 (giờ) (vì x > 0) ≈ 29 phút.

Vì hai vận động viên bắt đầu chạy từ 9 giờ, do đó thời điểm mà hai vận động viên cách nhau 10 km là khoảng: 9 giờ 29 phút.

Vậy vào khoảng 9 giờ 29 phút thì hai vận động viên sẽ cách nhau 10 km.

Học tốt Định lí côsin và định lí sin

Các bài học để học tốt Định lí côsin và định lí sin Toán lớp 10 hay khác:

• Giải sgk Toán 10 Bài 2: Định lí côsin và định lí sin