Thực hành 5 trang 93 Toán 10 Tập 1 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

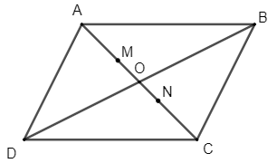
Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:

Giải Toán lớp 10 Bài 2: Tổng và hiệu của hai vectơ

Thực hành 5 trang 93 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:

a) $\vec{M A} + \vec{M D} + \vec{M B} = \vec{0}$ ;

b) $\vec{N D} + \vec{N B} + \vec{N C} = \vec{0}$ ;

c) $\vec{P M} + \vec{P N} = \vec{0}$ .

Lời giải:

Thực hành 5 trang 93 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán lớp 10

a) Gọi M là trọng tâm tam giác ADB.

Khi đó ta có: $\vec{M A} + \vec{M D} + \vec{M B} = \vec{0}$

Vậy điểm M thỏa mãn $\vec{M A} + \vec{M D} + \vec{M B} = \vec{0}$ là trọng tâm của tam giác ADB.

b) Tương tự câu a, điểm N thỏa mãn $\vec{N D} + \vec{N B} + \vec{N C} = \vec{0}$ là trọng tâm của tam giác DBC.

c) ABCD là hình bình hành có tâm O nên O là giao của hai đường chéo AC và BD, đồng thời là trung điểm của mỗi đường.

Khi đó AO là đường trung tuyến của tam giác ABD nên trọng tâm M của tam giác này nằm trên cạnh AO thỏa mãn AM = $\frac{2}{3}$ AO nên OM = $\frac{1}{3}$ AO.

Và CO là đường trung tuyến của tam giác BDC nên trọng tâm N của tam giác này nằm trên cạnh CO thỏa mãn CN = $\frac{2}{3}$ CO nên ON = $\frac{1}{3}$ CO.

Mà AO = CO.

Do đó: ON = OM.

Và O, M, N thẳng hàng (cùng thuộc đường chéo AC).

Nên O là trung điểm của MN.

Suy ra $\vec{O M} + \vec{O N} = \vec{0}$ .

Mà $\vec{P M} + \vec{P N} = \vec{0}$ nên điểm P trùng với điểm O.

Vậy điểm P thỏa mãn $\bar{P M} + \bar{P N} = \vec{0}$ là tâm O của hình bình hành ABCD.

Lời giải bài tập Toán 10 Bài 2: Tổng và hiệu của hai vectơ hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯