Bài 2.8 trang 58 Toán 12 Kết nối tri thức Tập 1

❮ Bài trước Bài sau ❯

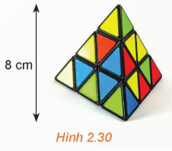
Trong Luyện tập 8, ta đã biết trọng tâm của tứ diện ABCD là một điểm I thỏa mãn , ở đó G là trọng tâm của tam giác BCD. Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8 cm (H.2.30).

Giải Toán 12 Bài 6: Vectơ trong không gian - Kết nối tri thức

Bài 2.8 trang 58 Toán 12 Tập 1: Trong Luyện tập 8, ta đã biết trọng tâm của tứ diện ABCD là một điểm I thỏa mãn $\vec{A I} = 3 \vec{I G}$ , ở đó G là trọng tâm của tam giác BCD. Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8 cm (H.2.30).

Bài 2.8 trang 58 Toán 12 Kết nối tri thức Tập 1

Lời giải:

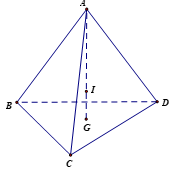
Giả sử khối rubik (đồng chất) hình tứ diện đều được mô phỏng như hình vẽ.

G là trọng tâm DBCD, I là trọng tâm của tứ diện

Vì ABCD là hình tứ diện đều nên AG $⊥$ (BCD) và AG = 8 cm.

Vì $\vec{A I} = 3 \vec{I G}$ nên 3 điểm A, I, G thẳng hàng và $I G = \frac{1}{4} A G$ .

Do đó IG $⊥$ (BCD). Khi đó $d (I, (B C D)) = I G = \frac{1}{4} A G = 2$ cm.

Lời giải bài tập Toán 12 Bài 6: Vectơ trong không gian hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯