HĐ3 trang 49 Toán 12 Kết nối tri thức Tập 1

❮ Bài trước Bài sau ❯

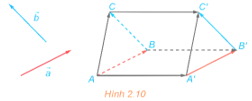
Trong không gian, cho hai vectơ và không cùng phương. Lấy điểm A và vẽ các vectơ , . Lấy điểm A' khác A và vẽ các vectơ (H.2.10).

Giải Toán 12 Bài 6: Vectơ trong không gian - Kết nối tri thức

HĐ3 trang 49 Toán 12 Tập 1: Trong không gian, cho hai vectơ $\vec{a}$ và $\vec{b}$ không cùng phương. Lấy điểm A và vẽ các vectơ $\vec{A B} = \vec{a}$ , $\vec{B C} = \vec{b}$ . Lấy điểm A' khác A và vẽ các vectơ $\vec{A^{'} B^{'}} = \vec{a}, \vec{B^{'} C^{'}} = \vec{b}$ (H.2.10).

a) Giải thích vì sao $\vec{A A^{'}} = \vec{B B^{'}}$ và $\vec{B B^{'}} = \vec{C C^{'}}$ .

b) Giải thích vì sao AA'C'C là hình bình hành, từ đó suy ra $\vec{A C} = \vec{A^{'} C^{'}}$ .

HĐ3 trang 49 Toán 12 Kết nối tri thức Tập 1

Lời giải:

a) Vì $\vec{A B} = \vec{a}$ và $\vec{A^{'} B^{'}} = \vec{a}$ nên $\vec{A B} = \vec{A^{'} B^{'}}$ .

Do đó ABB'A' là hình bình hành.

Suy ra AA' // BB' và AA' = BB'. Do đó $\vec{A A^{'}} = \vec{B B^{'}}$ .

Vì $\vec{B C} = \vec{b}$ và $\vec{B^{'} C^{'}} = \vec{b}$ nên $\vec{B C} = \vec{B^{'} C^{'}}$ .

Do đó BCC'B' là hình bình hành.

Suy ra BB' // CC' và BB' = CC'. Do đó $\vec{B B^{'}} = \vec{C C^{'}}$ .

b) Vì $\vec{A A^{'}} = \vec{B B^{'}}$ và $\vec{B B^{'}} = \vec{C C^{'}}$ nên $\vec{A A^{'}} = \vec{C C^{'}}$ .

Do đó ACC'A' là hình bình hành.

Do đó $\vec{A C} = \vec{A^{'} C^{'}}$ .

Lời giải bài tập Toán 12 Bài 6: Vectơ trong không gian hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯