15 Bài tập Góc và cạnh của một tam giác (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 7
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Góc và cạnh của một tam giác Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.
15 Bài tập Góc và cạnh của một tam giác (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 7
Chỉ từ 150k mua trọn bộ trắc nghiệm Toán 7 Chân trời sáng tạo (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa:
Câu 1. Trong một tam giác, tổng số đo ba góc bằng
A. 180°;
B. 90°;
C. 240°;
D. 120°.
Hiển thị đáp án
Đáp án đúng là: A
Trong một tam giác, tổng số đo ba góc bằng 180°.
Câu 2. Trong các khẳng định sau, khẳng định nào sai?
A. Tam giác vuông là tam giác có một góc vuông;
B. Tam giác nhọn là tam giác có ba góc nhọn;
C. Tam giác tù là tam giác có ba góc tù;
D. Trong tam giác vuông, tổng hai góc nhọn bằng 90°.
Hiển thị đáp án
Đáp án đúng là: C
Tam giác tù là tam giác có một góc tù.
Suy ra khẳng định C sai.
Câu 3. Cho tam giác ABC có A ^ = 45 o B ^ = 55 o
A. 45°;
B. 100°;
C. 90°;
D. 80°.
Hiển thị đáp án
Đáp án đúng là: D
Áp dụng định lý về tổng số đo ba góc của tam giác ta có:
A ^ + B ^ + C ^ = 180 °
Suy ra C ^ = 180 ° - A ^ - B ^ = 180 ° - 45 ° - 55 ° = 80 °
Câu 4. Cho tam giác ABC vuông tại A. Khi đó B ^ C ^
A. 180°;
B. 90°;
C. 100°;
D. 120°.
Hiển thị đáp án
Đáp án đúng là: B
Vì tam giác ABC vuông tại A nên tổng hai góc nhọn bằng 90° hay B ^ C ^
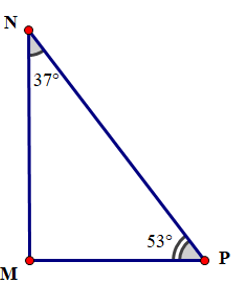
Câu 5. Cho tam giác MNP có số đo như hình vẽ:
Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I). M ^
(II). Tam giác MNP là tam giác nhọn.
(III). Tam giác MNP là tam giác vuông.
(IV). NP là cạnh huyền của tam giác MNP.
A. 1;
B. 2;
C. 3;
D. 4.
Hiển thị đáp án
Đáp án đúng là: B
Áp dụng định lý về tổng số đo ba góc của tam giác ta có:
M ^ + N ^ + P ^ = 180 °
Suy ra M ^ = 180 ° - N ^ - P ^ 180 ° - 37 ° - 53 ° = 90 °
Suy ra tam giác MNP vuông tại M
Ta có cạnh NP là cạnh đối diện với góc vuông M nên NP là cạnh huyền
Suy ra các khẳng định (III), (IV) đúng. Các khẳng định (I), (II) sai.
Vậy có 2 khẳng định đúng.
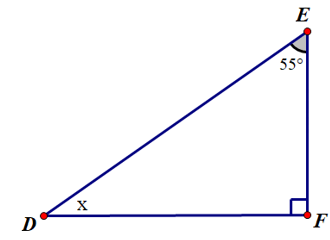
Câu 6. Cho hình vẽ sau:
Số đo x là:
A. 45°;
B. 40°;
C. 35°;
D. 30°.
Hiển thị đáp án
Đáp án đúng là: C
Vì tam giác DEF vuông tại F nên D ^ E ^
Suy ra D ^ E ^
Vậy x = 35°.
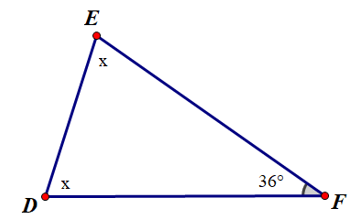
Câu 7. Cho hình vẽ sau:
Số đo x là:
A. 72°;
B. 73°;
C. 74°;
D. 75°.
Hiển thị đáp án
Đáp án đúng là: A
Áp dụng định lý về tổng số đo ba góc của tam giác ta có:
D ^ + E ^ + F ^ = 180 °
Suy ra x + x + 36° = 180°
Suy ra 2x = 144°
Suy ra x = 72°.
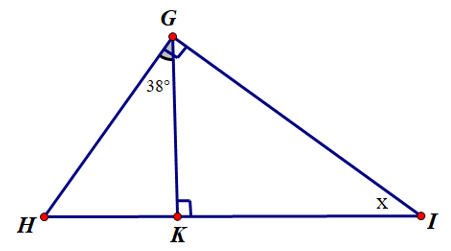
Câu 8. Tính số đo x trong hình sau:
A. 38°;
B. 52°;
C. 36°;
D. 62°.
Hiển thị đáp án
Đáp án đúng là: A
Ta có: H G K ^ K G I ^ H G I ^
Suy ra K G I ^ H G I ^ H G K ^ 90 ° - 38 ° = 52 °
Vì tam giác GKI vuông tại K nên K G I ^ G I K ^ °
Suy ra G I K ^ ° K G I ^ ° ° °
Vậy x = 38°.
Câu 9. Điền vào chỗ trống:
“Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng … độ dài cạnh còn lại”
A. lớn hơn;
B. nhỏ hơn;
C. bằng;
D. lớn hơn hoặc bằng.
Hiển thị đáp án
Đáp án đúng là: A
Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn
Câu 10. Cho tam giác MNP. Khẳng định nào sau đây đúng?
A. MN − NP = MP = MN + NP;
B. MN + NP < MP < MN – NP;
C. MN + NP > MP > MN – NP;
D. MN – NP > MP > MN + NP.
Hiển thị đáp án
Đáp án đúng là: C
Từ bất đẳng thức trong tam giác, ta có: MN + NP > MP; MN – NP < MP
Suy ra MN + NP > MP > MN – NP
Suy ra khẳng định C đúng. Các khẳng định A, B, D sai.
Câu 11. Trong các bộ ba đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?
A. 2 cm; 3 cm; 6 cm;
B. 3 cm; 6 cm; 3 cm;
C. 3 cm; 4 cm; 5 cm;
D. 5 cm; 6 cm; 7 dm.
Hiển thị đáp án
Đáp án đúng là: C
+ Xét bộ ba: 2 cm; 3 cm; 6 cm
Ta có 2 cm + 3 cm = 5 cm < 6 cm
Suy ra bộ ba đoạn thẳng có độ dài: 2 cm; 3 cm; 6 cm không lập thành một tam giác.
+ Xét bộ ba: 3 cm; 6 cm; 3 cm
Ta có 3 cm + 3 cm = 6 cm
Suy ra bộ ba đoạn thẳng có độ dài: 3 cm; 6 cm; 3 cm không lập thành một tam giác.
+ Xét bộ ba: 3 cm; 4 cm; 5 cm
Ta có: 4 cm – 3 cm < 5 cm < 4 cm + 3 cm
Suy ra bộ ba đoạn thẳng có độ dài: 3 cm; 4 cm; 5 cm lập thành một tam giác.
+ Xét bộ ba: 5 cm; 6 cm; 7 dm
Ta có 7 dm = 70 cm
Vì 5 cm + 6 cm < 70 cm
Suy ra bộ ba đoạn thẳng có độ dài: 5 cm; 6 cm; 7 dm không lập thành một tam giác.
Câu 12. Cho tam giác ABC có độ dài ba cạnh là ba số nguyên. Biết AB = 3 cm; AC = 7 cm. Khi đó độ dài cạnh BC không thể bằng
A. 4 cm;
B. 5 cm;
C. 6 cm;
D. 7 cm.
Hiển thị đáp án
Đáp án đúng là: A
Từ bất đẳng thức trong tam giác, ta có:
AC – AB < BC < AC + AB.
Suy ra 7 cm – 3 cm < BC < 7 cm + 3 cm.
Suy ra 4 cm < BC < 10 cm.
Suy ra BC không thể có độ dài bằng 4 cm.
Câu 13. Cho tam giác ABC có AB = 2, BC = 8 cm. Biết độ dài cạnh AC là một số nguyên tố. Chu vi tam giác ABC là:
A. 18 cm;
B. 7 cm;
C. 17 cm;
D. 19 cm.
Hiển thị đáp án
Đáp án đúng là: C
Gọi độ dài cạnh AC là x (x > 0) (cm)
Từ bất đẳng thức trong tam giác, ta có: BC – AB < AC < BC + AB
Suy ra 8 – 2 < x < 8 + 2
Suy ra 6 < x < 10
Suy ra x ∈ {7; 8; 9}
Vì x là một số nguyên tố
Suy ra x = 7
Suy ra AC = 7 (cm)
Chu vi tam giác ABC bằng:
AB + AC + BC = 2 + 7 + 8 = 17 (cm).
Câu 14. Cho tam giác ABC có A ^ = 40 o B ^ C ^ B ^ C ^
A.B ^ C ^
B.B ^ C ^
C.B ^ C ^
D.B ^ C ^
Hiển thị đáp án
Đáp án đúng là: C
Áp dụng định lý về tổng số đo ba góc của tam giác ta có:
A ^ + B ^ + C ^ = 180 °
Suy ra B ^ = 180 ° - A ^ - C ^ = 180 ° - 40 ° - C ^ = 140 ° - C ^
Ta có: B ^ - C ^ = 30 °
Suy ra 140 ° - C ^ - C ^ = 30 °
Suy ra 140 ° - 2 C ^ = 30 °
Suy ra 2C ^ °
Suy ra C ^ °
Suy ra B ^ = 140 ° - C ^ = 85 °
Vậy B ^ = 85 ° C ^ °
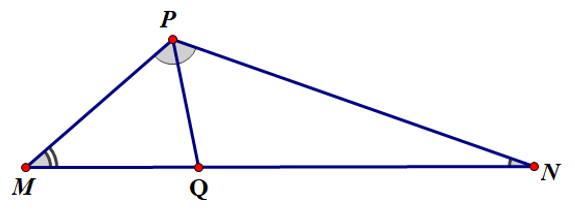
Câu 15. Cho tam giác MNP có M ^ N ^ 1 3 P ^ M P Q ^
A. 20°;
B. 60°;
C. 80°;
D. 120°.
Hiển thị đáp án
Đáp án đúng là: B
Vì 2 N ^ 1 3 P ^ P ^ N ^
Áp dụng định lý về tổng số đo ba góc của tam giác ta có:
M ^ + N ^ + P ^ = 180 °
Suy ra 2N ^ N ^ N ^ °
Suy ra 9N ^ °
Suy ra N ^ °
Suy ra P ^ N ^ ° °
Vì PQ là tia phân giác của M P N ^
M P Q ^ 1 2 M P N ^ 1 2 . 120 ° = 60 °