70 câu trắc nghiệm Tĩnh học vật rắn có lời giải chi tiết (nâng cao) - Vật Lí lớp 10

---

70 câu trắc nghiệm Tĩnh học vật rắn có lời giải chi tiết (nâng cao)

Với 70 câu trắc nghiệm Tĩnh học vật rắn có lời giải chi tiết (nâng cao) Vật Lí lớp 10 tổng hợp 70 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tĩnh học vật rắn từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 10.

Bài 1: Một tấm ván nặng 240N được bắc qua con mương. Trọng tâm của tấm ván cách điểm tựa A 2,4m, cách B 1,2m. Xác định lực mà tấm ván tác dụng lên 2 bờ mương.

A. 80 N, 160 N    B. 70 N, 150 N    C. 50 N, 100 N    D. 60 N, 130 N

Lời giải:

Đáp án: A

P = P₁ + P₂ = 240N → P₁ = 240 – P₂

P₁.d₁ = P₂.d₂ ↔ (240 – P₂).2,4 = 1,2P₂

↔ P₂ = 160N → P₁ = 80N.

Bài 2: Một thanh AB dài 2m đồng chất có tiết diện đều, m = 2kg. Người ta treo vào đầu A của thanh một vật m₁ = 5kg, đầu B một vật m₂ = 1kg. Hỏi phải đặt một giá đỡ tại điểm O cách đầu A một khoảng OA là bao nhiêu để thanh cân bằng.

A. 1 N    B. 0,5 N    C. 2 N    D. 1,5 N

Lời giải:

Đáp án: B

Áp dụng quy tắc momen lực: M_A = M_P + M_B

↔ P₁. OA = P. OI + P₂. OB

AI = IB = 1m

OI = AI – OA = 1 – OA

OB = OI – IB = 2 – OA

↔ 50. OA = 20 (1- OA) + 10(2 – OA) → OA = 0,5m.

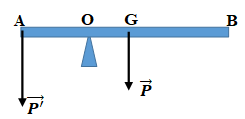
Bài 3: Thước AB = 100cm, trọng lượng P = 10N, trọng tâm ở giữa thước. Thước có thể quay dễ dàng xung quanh một trục nằm ngang đi qua O với OA = 30cm. Để thước cân bằng và nằm ngang, ta cần treo một vật tại đầu A có trọng lượng bằng bao nhiêu?

A. 4,38 N    B. 5,24 N    C. 6,67 N    D. 9,34 N

Lời giải:

Đáp án: C

Thanh cân bằng nằm ngang khi:

M_P’(O) = M_P(O) ↔ P’.OA = P. GO

Ở đây: OA = 30cm, OG = AB/2 – AO = 20cm

↔ P’ = P. GO/OA = 10. 20/30 = 6,67 N

Bài 4: Hai người khiêng một vật nặng 1200N bằng một đòn tre dài 1m, một người đặt điểm treo của vật cách vai mình 40cm. Bỏ qua trọng lượng của đòn tre. Mỗi người phải chịu một lực bao nhiêu?

A. 480 N, 720 N.    B. 450 N, 630 N    C. 385 N, 720 N    D. 545 N, 825 N

Lời giải:

Đáp án: A

Gọi d₁ là khoảng cách từ điểm treo đến vai d₁ = 40cm

P = P₁ + P₂ = 1200 ↔ P₁ = P – P₂ = 1200 – P₂

P₁.d₁ = P₂.d₂

↔ (1200 – P₂ ).0,4 = P₂. 0,6

→ P₂ = 480 N → P₁ = 720 N.

Bài 5: Một người gánh 2 thúng, thúng gạo nặng 300N, thúng ngô nặng 200N. Đòn gánh dài 1,5m. Hỏi vai người ấy phải đặt ở điểm nào để đòn gánh cân bằng và vai chịu một lực là bao nhiêu? Bỏ qua trọng lượng của đòn gánh.

A. cách đầu treo thúng gạo 60cm, vai chịu lực 500 N

B. cách đầu treo thúng gạo 30cm, vai chịu lực 300 N

C. cách đầu treo thúng gạo 20cm, vai chịu lực 400 N

D.cách đầu treo thúng gạo 50cm, vai chịu lực 600 N

Lời giải:

Đáp án: A

Gọi d₁ là khoảng cách từ thúng gạo đến vai, với lực P₁

d₂ là khoảng cách từ thúng ngô đến vai, với lực P₂

P₁.d₁ = P₂.d₂ ↔ 300d₁ = ( 1,5 – d₁).200

→ d₁ = 0,6m → d₂ = 0,9m

F = P₁ + P₂ = 500N.

Bài 6: Hai lực F₁→ , F₂→ song song cùng chiều, cách nhau đoạn 30cm. Một lực có F₁ = 18N, hợp lực F = 24 N. Điểm đặt của hợp lực cách điểm đặt của lực F₂ đoạn là bao nhiêu?

A. 11,5 cm.    B. 22,5 cm    C. 43,2 cm    D. 34,5 cm

Lời giải:

Đáp án: B

Hai lực // cùng chiều nên: F = F₁ + F₂ = 24 → F₂ = 6N

F₁.d₁ = F₂.d₂ ↔ 18(d – d₂ ) = 6d₂ → d₂ = 22,5 cm.

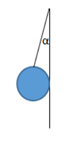
Bài 7: Một quả cầu đồng chất có khối lượng 5 kg được treo vào tường nhờ một sợi dây. Dây làm với tường một góc α = 60^o. Bỏ qua ma sát ở chổ tiếp xúc giữa quả cầu với tường. Hãy xác định lực căng của dây Lấy g = 10 m/s².

A. 25 N    B. 50 N    C. 75 N    D. 100 N

Lời giải:

Đáp án: D

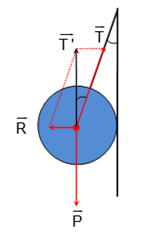
Các lực tác dụng lên quả cầu được biểu diễn như hình vẽ.

Điều kiện cân bằng của quả cầu là R→ + T→ = P'→ = -P→

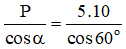
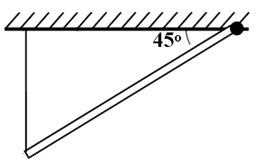
→ cosα = P/T → T = = 100 N.

Bài 8: Một quả cầu đồng chất có khối lượng 2 kg được treo vào tường nhờ một sợi dây. Dây làm với tường một góc 45^o. Bỏ qua ma sát ở chổ tiếp xúc giữa quả cầu với tường. Hãy xác định phản lực của tường. Lấy g = 9,8 m/s².

A. 20 N    B. 27,7 N    C. 19,6 N    D. 17 N

Lời giải:

Đáp án: C

Các lực tác dụng lên quả cầu được biểu diễn như hình vẽ

Điều kiện cân bằng của quả cầu là R→ + T→ = P'→ = -P→

→ tan α = R/P → R = Ptanα = 2.9,8.tan45^o = 19,6 N.

Bài 9: Một vật khối lượng 8 kg được giữa yên trên một mặt phẳng nghiêng bằng một sợi dây song song với mặt phẳng nghiêng. Góc nghiêng 45^o. Bỏ qua lực ma sát giữa vật và mặt phẳng nghiêng. Lấy g = 9,8 m/s². Xác định lực căng dây

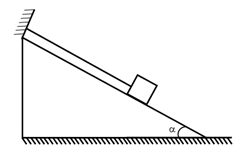
A. 78,4 N     B. 55,4 N    C. 75 N     D. 100,7 N

Lời giải:

Đáp án: B

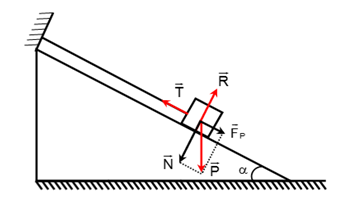
Các lực tác dụng lên vật là P→ , T→ , R→

Để vật cân bằng thì:

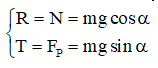
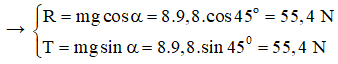
Bài 10: Một vật khối lượng 10 kg được giữu yên trên một mặt phẳng nghiêng bằng một sợi dây song song với mặt phẳng nghiêng. Góc nghiêng 30^o. Bỏ qua lực ma sát giữa vật và mặt phẳng nghiêng. Lấy g = 10 m/s². Xác định lực căng dây

A. 25 N    B. 50 N    C. 75 N    D. 100 N

Lời giải:

Đáp án: B

Các lực tác dụng lên vật là P→ , T→ , R→

Để vật cân bằng thì:

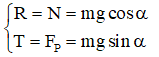
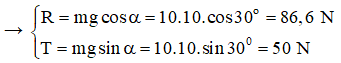
Bài 11: Một vật khối lượng m = 12 kg được giữ yên trên một mặt phẳng nghiêng bởi một sợi dây song song với đường dốc chính. Biết góc nghiêng α = 60^o, g = 10 m/s² và ma sát không đáng kể. Xác định phản lực của mặt phẵng nghiêng lên vật.

A. 30 N    B. 104 N    C. 60 N     D. 120 N

Lời giải:

Đáp án: C

Các lực tác dụng lên vật là P→ , T→ , R→

Để vật cân bằng thì:

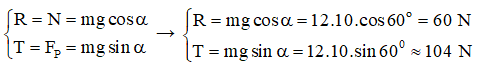
Bài 12: Một quả cầu đồng chất có khối lượng 25 kg được treo vào tường nhờ một sợi dây. Dây làm với tường một góc 30^o. Bỏ qua ma sát ở chổ tiếp xúc giữa quả cầu với tường. Hãy xác định lực căng của dây Lấy g = 9,8 m/s².

A. 150√3 N    B. 346 N    C. 283 N    D. 140 N

Lời giải:

Đáp án: C

Các lực tác dụng lên quả cầu được biểu diễn như hình

Điều kiện cân bằng của quả cầu là R→ + T→ = P'→ = -P→

→ cos α = P/T → T = 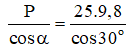≈ 283 N.

Bài 13: Một quả cầu đồng chất có khối lượng 5 kg được treo vào tường nhờ một sợi dây. Dây làm với tường một góc 20^o. Bỏ qua ma sát ở chổ tiếp xúc giữa quả cầu với tường. Hãy xác định phản lực của tường tác dụng lên quả cầu. Lấy g = 9,8 m/s².

A. 16 N     B. 17,8 N    C. 45 N     D. 18,7 N

Lời giải:

Đáp án: B

Các lực tác dụng lên quả cầu được biểu diễn như hình

Điều kiện cân bằng của quả cầu là R→ + T→ = P'→ = -P→

→ tan α = R/P → R = P.tan.α = 5.9,8.tan20^o = 17,8 N.

Bài 14: Hai mặt phẳng đỡ tạo với mặt phẳng nằm ngang các góc 45^o. Trên hai mặt phẳng đó người ta đặt một quả tạ hình cầu có khối lượng 5 kg. Bỏ qua ma sát và lấy g =10 m/s². Hỏi áp lực của quả cầu lên mỗi mặt phẳng đỡ bằng bao nhiêu ?

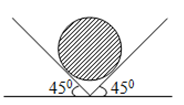
A. 25 N    B. 30 N    C. 50 N     D. 25√2 N

Lời giải:

Đáp án: D

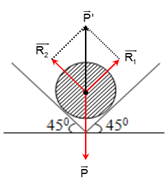
Các lực tác dụng lên quả tạ được biểu diễn như hình.

Điều kiện cân bằng của quả tạ là R₁→ + R₂→ = P'→ = -P→

Do hai góc nghiêng đều là 45^o nên R₁ = R₂ = P.cos45^o = 5.10.cos45^o = 25√2 N.

Bài 15: Một vật chịu tác dụng của ba lực đồng phẳng có độ lớn lần lượt là F₁, F₂, F₃ với F₁ = 2F₂ như hình vẽ. Muốn cho vật được cân bằng thì giữa F₁, F₂, F₃ phải thỏa mãn điều kiện nào sau đây ?

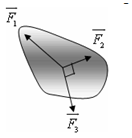
A. F₃ = (√3/2) F₁; F₂ = F₁/2    B. F₃ = F₁/3; F₂ = 2 F₁    C. F₃ = 3 F₁; F₂ = 2 F₁    D. F₃ = F₁/3; F₂ = F₁/2

Lời giải:

Đáp án: A

Để vật cân bằng thì F₁→ = F₂→ + F₃→

Lại có: F₁ = 2F₂ → 4F₂² = F₂² + F₃² → 3F₂² = F₃² → F₃ = F₂√3 → F₃ = 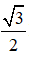F₁

F₁ = 2F₂ → F₂ = F₁/2.

Bài 16: Hai mặt phẳng đỡ tạo với mặt phẳng nằm ngang như hình. Trên hai mặt phẳng đó người ta đặt một quả tạ hình cầu có khối lượng 8 kg. Bỏ qua ma sát và lấy g = 10 m/ . Áp lực của quả cầu lên các mặt phẳng đỡ bằng

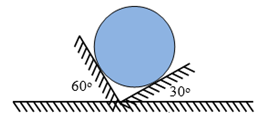
A. 40N; 40√3 N    B. 80N; 40√3 N    C. 40N; 40√2 N    D. 20N; 20√3 N

Lời giải:

Đáp án: A

Các lực tác dụng lên quả tạ được biểu diễn như hình

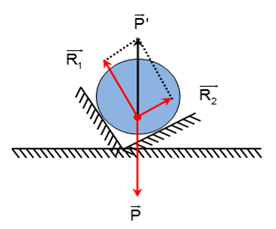
Điều kiện cân bằng của quả tạ là R₁→ + R₂→ = P'→ = -P→

Do 30^o + 60^o = 90^o → ( R₁→ , R₂→) = 90^o

→ R₁ = Pcos30^o = 8.10.cos30^o = 40√3 N

→ R₂ = Pcos60^o = 8.10.cos60^o = 40 N

Bài 17: Có ba viên gạch chồng lên nhau sao cho một phần của viên gạch trên nhô ra khỏi viên gạch dưới. Hỏi mép phải của viên gạch trên cùng có thể nhô ra khỏi mép phải của viên gạch cuối cùng một đoạn cực đại bằng bao nhiêu? Cho biết chiều dài viên gạch bằng l.

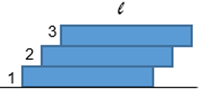
A. ℓ/2    B. ℓ /4    C. 3 ℓ /4    D. 2 ℓ /3

Lời giải:

Đáp án: C

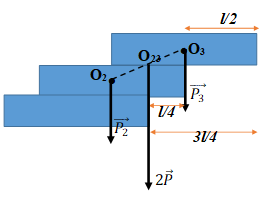
Gỉa sử viên gạch 2 không bị đổ thì viên gạch 3 chỉ được nhô ra khỏi viên gạch 2 nhiều nhất là ℓ/2

Dùng quy tắc hợp lực song song cùng chiều ta thấy trọng tâm G của hai viên gạch (2 và 3) cách đầu nhô ra của viên gạch 2 một đoạn ℓ/4. Do đó viên gạch 2 chỉ được nhô ra khỏi viên gạch 1 một đoạn lớn nhất là ℓ/4

Vậy so với viên gạch 1, viên gạch 3 được nhô ra nhiều nhất là .

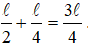
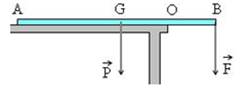
Bài 18: Một thanh sắt dài, đồng chất, tiết diện đều, được đặt trên bàn sao cho 1/4 chiều dài của nó nhô ra khỏi bàn. Tại đầu nhô ra, người ta đặt một lực F hướng thẳng đứng xuống dưới. Khi lực đạt tới giá trị 40 N thì đầu kia của thanh sắt bắt đầu bênh lên. Lấy g = 10 m/s². Tính khối lượng của thanh.

A. 20 N    B. 40 N    C. 80 N    D. 120 N

Lời giải:

Đáp án: B

Trục quay tại O.

Theo điều kiện cân bằng thì M_P/(O) = M_F/(O)

→ F.OB = P.OG ↔ 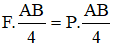→ P = F = 40 N.

Bài 19: Một thanh chắn đường AB dài 9 m, nặng 30 kg, trọng tâm G cách đầu B một khoảng BG = 6 m. Trục quay O cách đầu A một khoảng AO = 2 m, đầu A được treo một vật nặng. Người ta phải tác dụng vào đầu B một lực F = 100 N để giử cho thanh cân bằng ở vị trí nằm ngang. Tính khối lượng của vật nặng mà người ta đã treo vào đầu A. Lấy g = 10 m/s².

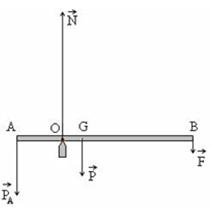
A. 30 kg    B. 40 kg    C. 50 kg    D. 60 kg

Lời giải:

Đáp án: C

Xét trục quay tai O.

Điều kiện cân bằng: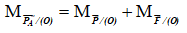

→ P_A.AO = P.OG + F.OB

→ m_A.2.10 = 30.10.1 + 100.7

→ m_A = 50 kg.

Bài 20: Một người nâng một tấm gỗ dài 1,5 m, nặng 30 kg và giữ cho nó hợp với mặt đất nằm ngang một góc 60^o. Biết trọng tâm của tấm gỗ cách đầu mà người đó nâng 120 cm, lực nâng vuông góc với tấm gỗ. Tính lực nâng của người đó.

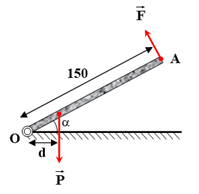
A. 300 N    B. 51,96 N    C. 240 N    D. 30 N

Lời giải:

Đáp án: D

Điều kiện cân bằng: M_F/(O) = M_P/(O)

→ P.d = F.OA ↔ mg.OG.cos60^o = F.OA

→ 30.10.30.0,5 = F.150

→ F = 30 N.

Bài 21: Một thanh gỗ dài 1,5 m nặng 12 kg, một đầu được gắn vào trần nhà nhờ một bản lề, đầu còn lại được buộc vào một sợi dây và gắn vào trần nhà sao cho phương của sợi dây thẳng đứng và giữ cho tấm gỗ nằm nghiêng hợp với trần nhà nằm ngang một góc 30o. Biết trọng tâm của thanh gổ cách đầu gắn bản lề 50 cm. Tính lực căng của sợi dây . Lấy g = 10 m/ .

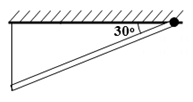
A. 120 N    B. 80 N    C. 40 N    D. 20 N

Lời giải:

Đáp án: C

Ta xét trục quay tại O.

Ta có điều kiện cân bằng: MT/(O) = MP/(O)

→ T.d’ = P.d

→ T.OA.cos30^o = P.OG.cos30^o

→ T.1,5 = 12.10.0,5

→ T = 40 N.

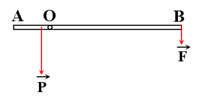
Bài 22: Một thanh chắn đường AB dài 7,5 m; có khối lượng 25 kg, có trọng tâm cách đầu A 1,2 m. Thanh có thể quay quanh một trục nằm ngang cách đầu A 1,5 m. Để giữ thanh cân bằng nằm ngang thì phải tác dụng lên đầu B một lực bằng bao nhiêu? Lấy g = 10 m/s² .

A. 125 N    B. 12,5 N    C. 26,5 N    D. 250 N

Lời giải:

Đáp án: B

Theo điều kiện cân bằng: M_F/(O) = M_P/(O)

→ F.OB = P.OG ↔ F(AB – OA) = P(OA – AG)

↔ F(7,5 – 1,5) = 25.10.(1,5 – 1,2)

→ F = 12,5 N.

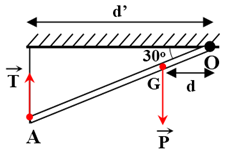
Bài 23: Một thanh gỗ dài 1,8 m nặng 30 kg, một đầu được gắn vào trần nhà nhờ một bản lề, đầu còn lại được buộc vào một sợi dây và gắn vào trần nhà sao cho phương của sợi dây thẳng đứng và giữ cho tấm gỗ nằm nghiêng hợp với trần nhà nằm ngang một góc 45^o. Biết trọng tâm của thanh gỗ cách đầu gắn sợi dây 60 cm. Tính lực căng của sợi dây . Lấy g = 10 m/s².

A. 300 N    B. 200 N    C. 240 N    D. 100 N

Lời giải:

Đáp án: B

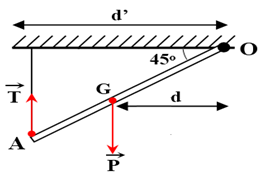
Điều kiện cân bằng M_T/(O) = M_P/(O)

→ T.d’ = P.d

→ T.OA.cos45^o = P.OG.cos45^o

→ T.1,8 = 30.10.1,2 → T = 200 N.

Bài 24: Đặt thanh AB có khối lượng không đáng kể nằm ngang, đầu A gắn vào tường nhờ một bản lề, đầu B nối với tường bằng dây BC. Treo vào B một vật có khối lượng 5 kg. Cho AB = 40 cm, AC = 60 cm như hình vẽ. Lấy g = 10 m/s2. Lực căng T của dây BC nhận giá trị nào sau đây ?

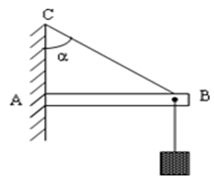
A. T = 50 N    B. T = 33,3 N    C. T = 80 N    D. T = 60 N

Lời giải:

Đáp án: D

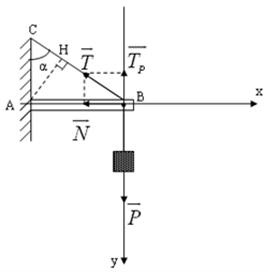
Ta có: BC = 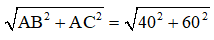= 72 cm

Điều kiện cân bằng:M_P = M_T → T.AH = P.AB

→ T = 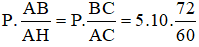= 60 N.

Bài 25: Hai lực song song cùng chiều cách nhau một đoạn 0,2 m. Nếu một trong hai lực có độ lớn 13 N và hợp lực của chúng có đường tác dụng cách lực kia một đoạn 0,08 m. Tính độ lớn của hợp lực và lực còn lại.

A. 7,5 N và 20,5 N    B. 10,5 N và 23,5 N    C. 19,5 N và 32,5 N    D. 15 N và 28 N

Lời giải:

Đáp án: C

Gọi d₁, d₂ là khoảng cách từ lực có độ lớn 13 N và lực còn lại đến hợp lực của chúng

→ d₁ + d₂ = 0,2

Mà d₂ = 0,08 m → d₁ = 0,2 – 0,08 = 1,12 m

Ta có: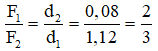

→ F₂ = 1,5F₁ = 1,5.13 = 19,5 N

→ F = F₁ + F₂ = 13 + 19,5 = 32,5 N

Bài 26: Hai người dùng một cái gậy để khiêng một cỗ máy nặng 100 kg. Điểm treo cỗ máy cách vai người thứ nhất 60 cm và cách vai người thứ hai 40 cm. Bỏ qua trọng lượng của gậy. Lấy g = 10 m/s². Hỏi mỗi người chịu một lực bằng bao nhiêu ?

A. 60 N và 40 N    B. 400 N và 600 N    C. 800 N và 1200 N    D. 500 N và 500 N

Lời giải:

Đáp án: B

Gọi F₁, F₂ là độ lớn của hai lực đặt lên hai đầu của cái gậy. F₁, F₂ lần lượt cách vai là d₁ = 60 cm, d₂ = 40 cm.

Ta có: F₁ + F₂ = mg = 1000 (1)

Và 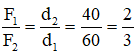→ 3F₁ – 2F₂ = 0 (2)

Từ (1) và (2) → F₁ = 400 N, F₂ = 600 N.

Bài 27: Một người đang quẩy trên vai một chiếc bị có trọng lượng 40 N. Chiếc bị buộc ở đầu gậy cách vai 70 cm, tay người giữ ở đầu kia cách vai 35 cm. Bỏ qua trọng lượng của gậy, để gậy cân bằng thì lực giữ gậy của tay phải bằng

A. 80 N    B. 100 N    C. 120 N    D. 160 N

Lời giải:

Đáp án: C

Gọi d₁, d₂ lần lượt là khoảng cách từ chiếc bị và tay người đến vai của người.

Tay người tác dụng lên chiếc gậy một lực là F_tay

Ta có: d₁ = 70 cm, d₂ = 35 cm

→ → F_tay = 2P = 2.40 = 80 N

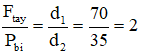
→ Vai người chịu tác dụng của lực bằng F_tay = F_tay + P_bi = 80 + 40 = 120 N.

Bài 28: Một tấm ván nặng 240 N được bắc qua một con mương. Trọng tâm của tấm ván cách điểm tựa A 2,4 m và cách điểm tựa B 1,2 m. Hỏi lực mà tấm ván tác dụng lên điểm tựa A bằng bao nhiêu ?

A. 240 N    B. 160 N    C. 80 N    D. 60 N

Lời giải:

Đáp án: C

Gọi F_A, F_B lần lượt là các lực do tấm ván tác dụng lên các điểm tựa A, B.

→ F_A + F_B = P = 240 (1)

Ta có: 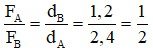→ 2F_A – F_B = 0 (2)

Từ (1), (2) → F_A = 80 N, F_B = 160 N.

Bài 29: Một thanh đồng chất dài L, trọng lượng P được treo năm ngang bằng hai dây. Dây thứ nhất buộc vào đầu bên trái của thanh, dây thứ hai buộc vào điểm cách đầu bên phải L/4. Lực căng của dây thứ hai bằng bao nhiêu ?

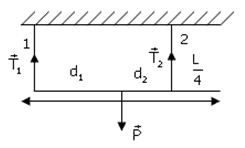
A. 2P/3    B. P/3    C. P/4    D. P/2

Lời giải:

Đáp án: A

Theo quy tắc hợp lực song song cùng chiều → T₁ + T₂ = P (1)

Lại có: 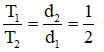→ 2T₁ – T₂ = 0 (2)

Từ (1) và (2) → T₁ = P/3, T₂ = 2P/3

Bài 30: Hai người cùng khiêng một thanh dầm bằng gỗ nặng, có chiều dài L. Người thứ hai khỏe hơn người thứ nhất. Nếu tay của người thứ nhất nâng một đầu thanh thì tay của người thứ hai phải đặt cách đầu kia của thanh một đoạn bằng bao nhiêu để người thứ hai chịu lực lớn gấp đôi người thứ nhất ?

A. L/3    B. L/4    C. 2L/5    D. 0

Lời giải:

Đáp án: B

Gọi F₁, F₂ lần lượt là lực nâng của tay người thứ nhất và người thứ hai → F₂ = 2F₁

d₁, d₂ là khoảng cách từ tay của hai người đến vị trí trọng tâm của thanh dầm → d₁ = L/2

Ta có: 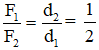= → d₂ = d₁/2 = L/4

Bài 31:Một thanh cứng có trọng lượng không đáng kể, được treo nằm ngang nhờ hai lò xo thẳng đứng có chiều dài tự nhiên bằng nhau. Độ cứng của hai lò xo lần lượt là k₁ = 160 N/m và k₂ = 100 N/m. Khoảng cách AB giữa hai lò xo là 75 cm. Hỏi phải treo một vật nặng vào điểm C cách đầu A bao nhiêu để thanh vẫn nằm ngang ?

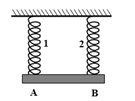
A. 45 cm    B. 30 cm    C. 50 cm    D. 25 cm

Lời giải:

Đáp án: B

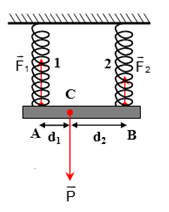
Thanh chịu ba lực song song cân bằng. Muốn cho thanh vẫn nằm ngang thì hai lò xo phải dãn ra như nhau.

(1)

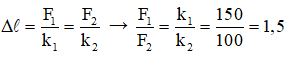
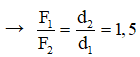
Lại có: d₁ + d₂ = 75 (2)

Từ (1) và (2) → d₁ = CA = 30 cm, d₂ = CB = 45 cm.

Bài 32: Hai lực song song cùng chiều, có độ lớn F₁ = 5 N, F₂ = 15 N đặt tại hai đầu một thanh nhẹ (khối lượng không đáng kể) AB dài 20 cm. Hợp lực F→ = F₁→ + F₂→ đặt cách đầu A bao nhiêu và có độ lớn bằng bao nhiêu ?

A. OA = 15 cm, F = 20 N

B. OA = 5 cm, F = 20 N

C. OA = 15 cm, F = 10 N

D. OA = 5 cm, F = 10 N

Lời giải:

Đáp án: A

Gọi d₁, d₂ là khoảng cách từ các lực F₁→ , F₂→ đến hợp lực F→

Ta có: d₁ + d₂ = 20 (1)

Mặt khác: (1) → d₁ – 3d₂ = 0 (2)

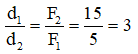
Từ (1) và (2) → d₁ = 15 cm, d₂ = 5 cm.

Hợp lực có độ lớn F = 5 +15 = 20 N.

Bài 33: Một thanh AB dài 1 m khối lượng 5 kg được đặt nằm ngang lên hai giá đỡ tại A và B. Người ta móc vào điểm C của thanh (AC = 60 cm) một trọng vật có khối lượng 10 kg. Lấy g = 10 m/s², lực nén lên hai giá đỡ là

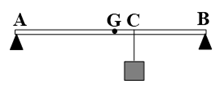
A. F₁ = 40 N, F₂ = 60 N

B. F₁ = 65 N, F₂ = 85 N

C. F₁ = 60 N, F₂ = 80 N

D. F₁ = 85 N, F₂ = 65 N

Lời giải:

Đáp án: B

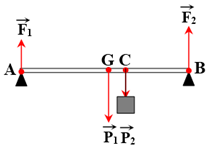
Phân tích các lực tác dụng lên thanh AB như hình.

→ F₁ + F₂ = P₁ + P₂ = 150 (1)

Gọi d₁, d₂ khoảng cách từ các lực P₁→ , P₂→ tới vị trí trọng tâm mới của vật: d₁ + d₂ = 10 cm (1)

Lại có: 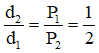→ d₁ – 2d₂ = 0 (2)

Từ (1) và (2) → d₁ = 20/3 cm, d₂ = 10/3 cm

→ Khoảng cách từ các lực F₁→ , F₂→ đến trọng tâm mới của vật là

d₁ = 50 + 20/3 = 170/3 cm, d₂ = 100 – 170/3 = 130/3 cm

→ 17F₁ – 13F₂ = 0 (3)

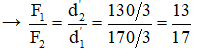
Từ (1), (3) → F₁ = 65 N, F₂ = 85 N.

Bài 34: Hai người dùng một cái đòn tre để khiêng một cái hòm có trọng lượng 500 N. Khoảng cách giữa vai của hai người là A₁A₂ = 2 m. Bỏ qua trọng lực của đòn thì cần treo hòm vào điểm nào thì lực đè lên vai người một sẽ lớn hơn lực đè lên vai người thứ hai là 100 N ?

A. OA₁ = 60 cm, OA₂ = 140 cm

B. OA₁ = 70 cm, OA₂ = 130 cm

C. OA₁ = 80 cm, OA₂ = 120 cm

D. OA₁ = 90 cm, OA₂ = 110 cm

Lời giải:

Đáp án: C

Ta có: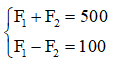

→ F₁ = 300 N, F₂ = 200 N.

Lại có: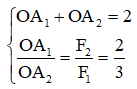

→ OA₁ = 80 cm, OA₂ = 120 cm.

Bài 35: Hai lực song song cùng chiều có độ lớn 20 N và 30 N đặt tại hai đầu của một thanh AB nhẹ khối lượng không đáng kể dài 20 cm. Hợp của hai lực này cách đầu A của thanh một khoảng bằng

A. 12 cm    B. 8 cm    C. 14 cm    D. 16 cm

Lời giải:

Đáp án: A

Ta có: 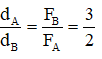(1)

Lại có: d_A + d_B = 20 (2)

Từ (1) và (2) → d_A = 12 cm, d_B = 8 cm.

Bài 36: Tính momen của lực đối với trục quay O, cho biết F = 100 N, OA = 100 cm. Bỏ qua trọng lượng của thanh.

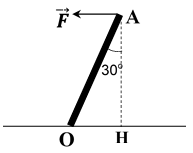
A. 50 N.m    B. 50√3 N.m    C. 100 N.m    D. 10√3 N.m

Lời giải:

Đáp án: B

Momen của lực là M = F.AH = 100.1.cos30^o = 50√3 N.m

Bài 37: Người ta khoét một lỗ tròn bán kính R/2 trong một đĩa tròn đồng chất bán kính R. Trọng tâm của phần còn lại cách tâm đĩa tròn lớn bao nhiêu ?

A. R/2    B. R/4    C. R/3    D. R/6

Lời giải:

Đáp án: D

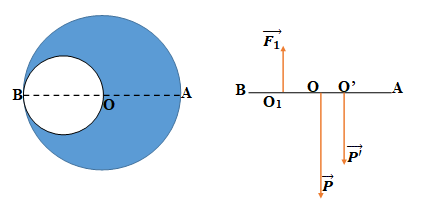
Sử dụng quy hợp lực song song ngược chiều. Ta được:

F₁.O₁O' = P.OO' ( ở đây ta coi F₁ giống như một lực nâng có độ lớn bằng trọng lượng phần khoét đi lên biểu thị cho phần lỗ tròn rỗng, và P là trọng lực của cả đĩa tròn khi chưa khoét)

(x = OO’)

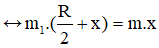
Đĩa tròn đồng chất 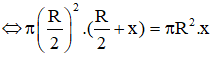→ x = OO’ = R/6

Bài 38: Ba lực đồng quy tác dụng lên vật rắn cân bằng có độ lớn lần lượt là 12N, 16N và 20N. Nếu lực 16N không tác dụng vào vật nữa thì hợp lực tác dụng lên vật là:

A. 16N.    B. 20N.    C. 15N.    D. 12N.

Lời giải:

Đáp án: A

Vật rắn cân bằng nên các lực tác dụng lên vật triệt tiêu:

(1)

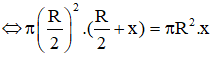
Bỏ lực 16N đi thì vật chịu lực là hợp lực của 2 lực 12N và 20N.

Theo (1), suy ra hợp lực của lực 12 N và 20 N là lực có chiều ngược chiều với chiều lực 16 N và có độ lớn bằng 16 N.

Bài 39: Một thanh AB = 7,5m có trọng lượng 200N có trọng tâm G cách đầu A một đoạn 2m. Thanh có thể quay xung quanh một trục đi qua O. Biết OA = 2,5m. Hỏi phải tác dụng vào đầu B một lực F có độ lớn bằng bao nhiêu để AB cân bằng?

A. 100N.    B. 25N.    C. 10N.    D. 20N.

Lời giải:

Đáp án: D

P.GO = F.OB ⇔ 200.0,5 = F(7,5 - 2,5) → F = 20(N)

Bài 40: Một thanh AB có trọng lượng 150N có trọng tâm G chia đoạn AB theo tỉ lệ BG = 2 AG. Thanh AB được treo lên trần bằng dây nhẹ, không giãn (Hình bên). Cho góc  = 300. Tính lực căng dây T?

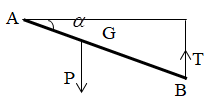
A. 75N.    B. 100N.    C. 150N.    D. 50N.

Lời giải:

Đáp án: D

Thanh có thể quay quanh A: P.AG.cosα = T. AB cosα

⇔ T = P. AG/AB = P/3 – 150/3 = 50 N.

Bài 41: Cho một hệ gồm hai chất điểm m₁=0,05kg đặt tại điểm P và m₂=0,1kg đặt tại điểm Q. Cho PQ = 15cm. Trọng tâm của hệ

A. nằm ngoài khoảng PQ

B. cách P một khoảng 10cm và cách Q một khoảng 5cm

C. cách P một khoảng 5cm

D. cách Q một khoảng 10cm

Lời giải:

Đáp án: B

Ta có: P₁.PG = P₂.GQ

⇔ PG/GQ = P₂/P₁ = m₂/m₁ = 2

và PG + GQ = 15

⇒ PG = 10(cm); GQ = 5 (cm)

Bài 42: Có 3 viên gạch giống nhau, mỗi viên có chiều dài L. Ba viên gạch này được xếp chồng lên nhau sao cho viên gạch trên đua ra một phần so với viên gạch dưới. Chiều dài lớn nhất của chồng gạch mà không bị đổ là

A. 5L/4    B. 7L/4    C. 2L    D. 1,5L

Lời giải:

Đáp án: B

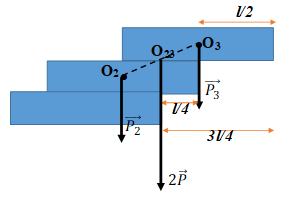
Viên gạch thứ 3 có thể nhô ra L/2 là khoảng cách lớn nhất. Hệ 2 viên gạch (2) và (3) nằm cân bằng thì hợp lực 2P→ như hình vẽ.

⇒ y = L/4

→ Chiều dài lớn nhất của chồng gạch là: L = L/4 + L/2 = 7L/4

Bài 43:Thanh AC đồng chất có trọng lượng 4N, chiều dài 8cm. Biết quả cân P₁=10N treo vào đầu A, quả cân P₂ treo vào đầu C. Trục quay cách A 2cm, hệ cân bằng. Hỏi P₂ có độ lớn là bao nhiêu?

A. 5N    B. 4,5N    C. 3,5N    D. 2N

Lời giải:

Đáp án: D

Ta có: P₁.AO = P_AB.OG + P₂.OB

↔ m₁.AO = mAB.OG + m₂.OB

→ P₂ = 2(N)

Bài 44: Có đòn bẩy như hình vẽ. Đầu A của đòn bẩy treo một vật có trọng lượng 30 N. Chiều dài đòn bẩy dài 50 cm. Khoảng cách từ đầu A đến trục quay O là 20 cm. Vậy đầu B của đòn bẩy phải treo một vật khác có trọng lượng là bao nhiêu để đòn bẩy cân bằng như ban đầu?

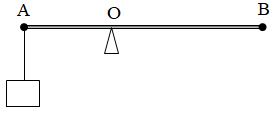
A.15 N     B. 20 N C. 25 N     D. 30 N

Lời giải:

Đáp án: B

Ta có: OB.P_B = OA.P_A ⇒ P_B = = 20 N.

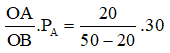
Bài 45: Một vật rắn phẳng mỏng dạng một tam giác đều ABC, cạnh a = 20cm. Người ta tác dụng vào một ngẫu lực năng trong mặt phẳng của tam giác. Các lực có độ lớn 8N và đặt vào hai đỉnh A và C và song song với BC. Momen của ngẫu lực là:

A. 13,8 Nm     B. 1,38 Nm    C. 13,8.10^-2Nm     D. 1,38.10^-3Nm

Lời giải:

Đáp án: B

M = F.d (F; độ lớn của lực)

d: Khoảng cách giữa 2 giá của lực

→ M = 8.a sin 60^o = 8.0,2 .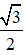 = 1,38 N/m.

Bài 46: Câu 46. Một cái xà nằm ngang chiều dài 10m trọng lượng 200N, Một đầu xà gắn vào tường đầu kia được giữ bằng sợi dây làm với phương nằm ngang góc 60^o. Sức căng của sợi dây là

A. 200N    B. 100N    C. 115,6N    D. 173N

Lời giải:

Đáp án: C

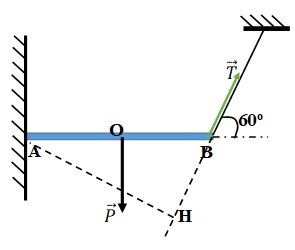
Xét trục quay tại A

Ta có: P.AO = T.AH

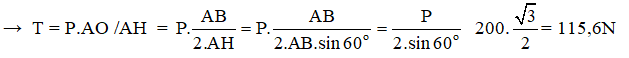
Bài 47: Có ba quả cầu nhỏ đồng chất khối lượng m₁, m₂ và m₃ được gắn theo thứ tự tại các điểm A, B và C trên một thanh AC hình trụ mảnh, cứng, có khối lượng không đáng kể, sao cho thanh xuyên qua tâm của các quả cầu. Biết m₁ = 2m₂ = 2M và AB = BC. Để khối tâm của hệ nằm tại trung điểm của AB thì khối lượng m₃ bằng

A. 2M/3.    B. M.    C. M/3    D. 2M.

Lời giải:

Đáp án: C

m₁ = 2M, m₂ = M

Để khối tâm của hệ tại trung điểm AB (GA =GB) thì:

m₁. AG = m₂. GB + m₃ GC ⇔ 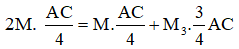⇔ m₃ = M/3

Bài 48: Có ba chất điểm 5kg, 4kg và 3kg được đặt trong hệ toạ độ 0xy. Vật 5kg có toạ độ (0,0); 3kg có toạ độ (0,4); 4kg có toạ độ (3,0). Hỏi phải đặt vật 8kg ở đâu để khối tâm của hệ trùng với gốc toạ độ (0,0)

A. x = 1,5; y = 1,5     B. x = -1,2; y = 1,5    C. x = -1,5; y = -1,5     D. x = -2,1; y = 1,8

Lời giải:

Đáp án: C

Sử dụng công thức tính tọa độ khối tâm của hệ vật ta được:

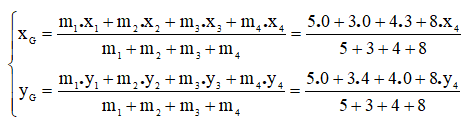
Để khối tâm của hệ trùng với gốc toạ độ (0,0) thì x_G = 0, y_G = 0.

→x₄ = -3/2; y₄ = -3/2

Bài 49: Thanh OA = 60cm có trọng lượng P₁ = 40N được giữ nằm ngang nhờ bản lề tại O và dây treo AD. Tại B (AB = 20cm) người ta treo vật nặng P₂ = 60N. Biết α = 45^o. Tính momen lực P₂ đối với O.

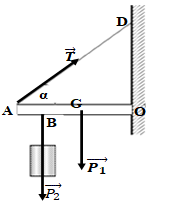
A. 24 N.m    B. 36 N.m    C. 12 N.m    D. 18 N.m

Lời giải:

Đáp án: A

Ta có: 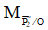= P₂.BO = P₂.(AO-AB) = 60.(0,6-0,2) = 24 N.m

Bài 50: Một người dùng búa để nhổ một chiếc đinh, khi người đó tác dụng một lực 50N vào đầu búa thì định bắt đầu chuyển động. Biết cánh tay đòn của lực tác dụng của người đó là 20cm và của lực nhổ đinh khỏi gỗ là 2cm. Hãy tính lực cản của gỗ tác dụng vào đinh.

A. 500 N    B. 400 N    C. 350 N    D. 200 N

Lời giải:

Đáp án: A

Điều kiện cân bằng: M_thuan = M_nghich ↔ F₁d₁ = F₂d₂

→ F₂ = 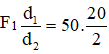= 500 N.

Bài 51: Hai lực F₁ và F₂ song song, ngược chiều đặt tại hai đầu thanh AB có hợp lực F đặt tại O cách A là 8 cm, cách B 2 cm và có độ lớn F = 10,5 N. Tìm F₁ và F₂.

A. 3,5 N và 14 N    B. 14 N và 3,5 N    C. 7 N và 3,5 N    D. 3,5 N và 7 N

Lời giải:

Đáp án: A

F = |F₁ – F₂|

F₁.8 = F₂.2 ⇒ F₂ = 4F₁ ⇒ F= 3F₁ ⇒ F₁ = 3,5 N và F₂ = 14 (N)

Bài 52: Một sợi dây cáp khối lượng không đáng kể, được căng ngang giữa hai cột thẳng đứng cách nhau 8 m. Ở điểm giữa của dây người ta treo một vật nặng khối lượng 6 kg, làm dây võng xuống 0,5 m. Lấy g = 10 m/s². Tính lực căng của dây.

A. 240 N    B. 320 N    C. 480 N    D. 160 N

Lời giải:

Đáp án: A

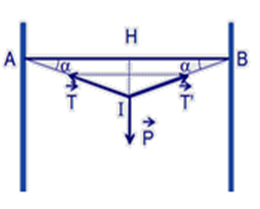
Điểm giữa của sợi dây chịu tác dụng của các lực:

Trọng lực P→ và các lực căng T→ , T'→ của sợi dây; với T’ = T.

Điều kiện cân bằng: P→ + T→ + T'→ = 0→.

Chiếu lên phương thẳng đứng, chiều dương từ trên xuống, ta có:

P - Tsinα - T’sinα = P - 2Tsinα = 0

→ T = 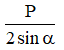= 240 N.

(với α rất nhỏ, sinα ≈ tanα = 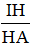= 0,125).

Bài 53: Một vật có khối lượng 2kg được giữ yên trên mặt phẳng nghiêng bởi một sợi dây song song với đường dốc chính (hình vẽ). Biết α = 30^o, g = 9,8m/s² và ma sát không đáng kể. Tính lực căng của dây?

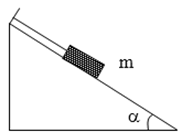
A. 10 N    B. 23 N    C. 15 N    D. 13 N

Lời giải:

Đáp án: A

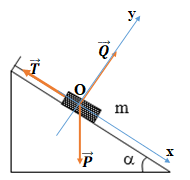
Các lực đồng quy tác dụng lên vật m trên hình.

Điều kiện cân bằng của m: P→ + Q→ + T→ = 0→. (*)

Chiếu (*) lên các trục

   Ox: Psinα - T = 0 (1)

   Oy: Q - Pcosα = 0 (2)

Lực căng T của sợi dây: T = Psinα = mgsin30^o = 2.10.1/2 = 10N.

Bài 54:Một vật có khối lượng 2kg được giữ yên trên mặt phẳng nghiêng bởi một sợi dây song song với đường dốc chính (hình vẽ). Biết α = 30^o, g = 9,8m/s² và ma sát không đáng kể. Tính phản lực của mặt phẳng nghiêng lên vật?

A. 10√2 N    B. 10√3 N    C.15√2 N    D. 15√3 N

Lời giải:

Đáp án: A

Các lực đồng quy tác dụng lên vật m trên hình.

Điều kiện cân bằng của m: P→ + Q→ + T→ = 0→. (*)

Chiếu (*) lên các trục

   Ox: Psinα - T = 0 (1)

   Oy: Q - Pcosα = 0 (2)

Phản lực Q của mặt phẳng nghiêng lên vật:

(2) → Q = P.cosα = m.g.cos30^o = 2.10.√3/2 = 10√3 N

Bài 55: Bánh xe có bán kính R = 50cm, khối lượng m = 50kg (hình vẽ). Tìm lực kéo tối thiểu F nằm ngang đặt trên trục để bánh xe có thể vượt qua bậc có độ cao h = 30cm. Bỏ qua ma sát. Lấy g = 10m/s².

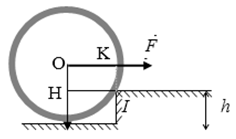
A. 2085 N    B. 1586 N    C. 1238 N    D. 1146 N

Lời giải:

Đáp án: D

-Các lực tác dụng lên bánh xe bao gồm:

Lực kéo F→ , Trọng lực P→ , Phản lực của sàn Q→ tại điểm I

-Điều kiện để bánh xe có thể lăn lên bậc thềm là:

M_F ≥ M_P (đối với trục quay tạm thời qua I, M_Q/(O) = 0 )

F.IK ≥ P.IH với IK= R – h;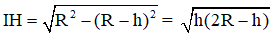

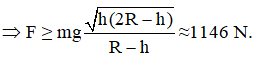
Bài 56:Để giữ thanh nặng OA có thể nằm nghiêng với sàn một góc α = 30^o, ta kéo đầu A bằng sợi dây theo phương vuông góc với thanh, còn đầu O được giữ bởi bản lề. Biết thanh OA đồng chất, tiết diện đều trọng lượng là P = 400N. Tính độ lớn lực kéo F.

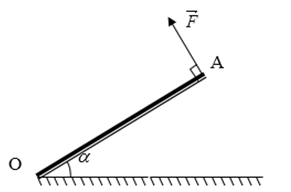
A. 100 N    B. 100 N    C. 150 N    D. 150 N

Lời giải:

Đáp án: B

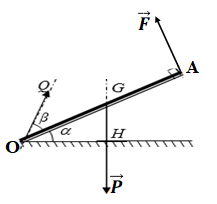
Điều kiện cân bằng của OA là:

   M_F = M_P (vì M_Q/(O) = 0)

↔F.OA = P.OH

với OH = OG.cosα = 0,5. OA.cosα

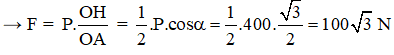
Bài 57: Để giữ thanh nặng OA có thể nằm nghiêng với sàn một góc α = 30^o, ta kéo đầu A bằng sợi dây theo phương vuông góc với thanh, còn đầu O được giữ bởi bản lề. Biết thanh OA đồng chất, tiết diện đều trọng lượng là P = 400N. Phản lực Q hợp với thanh OA một góc bằng bao nhiêu?

A. 36^o    B. 53^o    C. 26^o    D. 41^o

Lời giải:

Đáp án: D

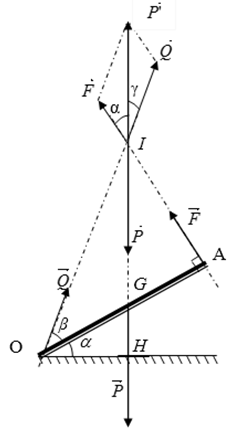
Điều kiện cân bằng của OA là: M_F = M_P (vì M_Q = 0)

F.OA = P.OH với OH = OG.cosα = 0,5. OA.cosα

→ F = 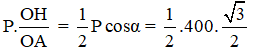= 100√3 N.

Do thanh OA không chuyển động tịnh tiến nên ta có điều kiện cân bằng là:

P→ + F→ + Q→ = 0→.

Các lực P→ , F→ có giá đi qua I, nên Q→ cũng có giá đi qua I. Trượt các lực P→, F→ , Q→ về điểm đồng quy I như hình vẽ, theo định lý hàm số cosin ta có:

Q² = F² + P² – 2F.P.cosα

= (100√3)² + 400² – 2.100√3.400.√3/2 ≈ 265N

Theo định lý hàm số sin ta có:

với γ = π/2 – (α+β)

→ ≈ 0,327

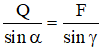
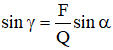
→ γ ≈ 19^o ⇒ β = π/2 - γ - α ≈ 90^o - 19^o - 30^o

→ β ≈ 41^o

Bài 58: Thanh OA có khối lượng không đáng kể, có chiều dài 20cm, quay dễ dàng quanh trục nằm ngang O. Một lò xo gắn vào điểm giữa C. Người ta tác dụng vào đầu A của thanh một lực F = 20N hướng thẳng đứng xuống dưới. Khi thanh ở trạng thái cân bằng, lò xo có hướng vuông góc với OA, và OA làm với đường nằm ngang một góc α = 30^o. Tìm phản lực N của lò xo lên thanh.

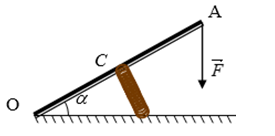
A. 45√2 N    B. 20√3 N    C. 20√2 N    D. 35√3 N

Lời giải:

Đáp án: B

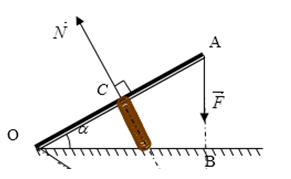
Ta vận dụng quy tắc mô men lực để tìm N. Điều kiện cân bằng của thanh OA quanh trục O là:

    M_F = M_N

↔ F.OB = N.OC với OB = 2OC.cosα

→ N = F.OB/OC = 2F.cosα = 2.20.√3/2 = 20√3 N

Bài 59: Thanh OA có khối lượng không đáng kể, có chiều dài 20cm, quay dễ dàng quanh trục nằm ngang O. Một lò xo gắn vào điểm giữa C. Người ta tác dụng vào đầu A của thanh một lực F = 20N hướng thẳng đứng xuống dưới. Khi thanh ở trạng thái cân bằng, lò xo có hướng vuông góc với OA, và OA làm với đường nằm ngang một góc α = 30^o. Tính độ cứng k của lò xo, biết lò xo ngắn đi 8cm so với lúc không bị nén.

A. 433 N/m    B. 526 N/m    C. 348 N/m    D. 276 N/m

Lời giải:

Đáp án: A

Ta vận dụng quy tắc mô men lực để tìm N.

Điều kiện cân bằng của thanh OA quanh trục O là:

    M_F = M_N ↔ F.OB = N.OC với OB = 2OC.cosα

→ N = F.OB/OC = 2F.cosα = 2.20.√3/2 = 20√3 N

Mặt khác: N = k.Δl

⇒k = N/Δl = 20√3/(8.10^-2) = 433 N/m

Bài 60: Thanh OA có khối lượng không đáng kể, có chiều dài 20cm, quay dễ dàng quanh trục nằm ngang O. Một lò xo gắn vào điểm giữa C. Người ta tác dụng vào đầu A của thanh một lực F = 20N hướng thẳng đứng xuống dưới. Khi thanh ở trạng thái cân bằng, lò xo có hướng vuông góc với OA, và OA làm với đường nằm ngang một góc α= 30^o. Tìm độ lớn phản lực Q của trục lên thanh OA.

A. 10√2 N    B. 20 N    C. 15√2 N    D. 15 N

Lời giải:

Đáp án: B

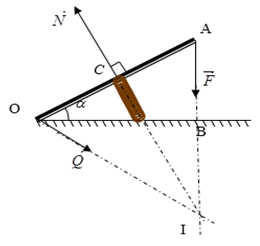
Điều kiện cân bằng lực là: F→ + N→ + Q→ = 0→.

Do các lực tác dụng lên OA có giá đồng quy nên, giá của Q→ cũng phải đi qua I.

Dễ thấy ΔOAI cân tại I nên Q = F = 20N.

Bài 61: Một thanh nhẹ gắn vào sàn tại B. Tác dụng lên đầu A lực kéo F = 100N theo phương ngang. Thanh được giữ cân bằng nhờ dây AC. Biết α = 30^o. Tính lực căng dây AC?

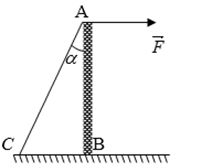
A. 250 N    B. 100 N    C. 200 N    D. 150 N

Lời giải:

Đáp án: C

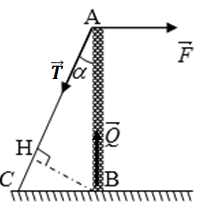
Xét trục quay tạm thời tại B (M_Q = 0), điều kiện cân bằng của thanh AB là:

M_F = M_T

↔ F.AB = T.BH với BH = AB.sinα = AB/2

→ = 2F = 200 N.

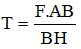
Bài 62: Một giá treo được bố trí như hình vẽ: Thanh nhẹ AB tựa vài tường ở A, dây BC không dãn nằm ngang, tại B treo vật có khối lượng m. Biết góc α = 45°, độ lớn của phản lực do tường tác dụng lên thanh là 24N. Tìm khối lượng m và sức căng T của dây. Lấy g = 10m/s2.

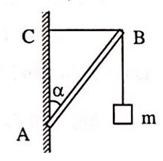
A. m = 1,69kg, T = 16,9N

B. m = 2,29kg, T = 6,9N

C. m = 1,97kg, T = 16,2N

D. m = 4,69kg, T = 46,9N

Lời giải:

Đáp án: A

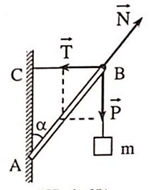
Các lực tác dụng lên thanh AB (tại B) như hình vẽ.

Điều kiện cân bằng: P→ + N→ + T→ = 0→.

Từ hệ thức lượng trong tam giác vuông thu được:

Trọng lực P = mg = Ncosα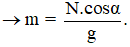

Thay số ta được: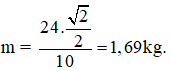

Vì α = 45° nên lực căng dây T = P =mg = 16,9N

Bài 63: Xác định vị trí trọng tâm của bản mỏng đồng chất như hình vẽ. Chọn đáp án đúng.

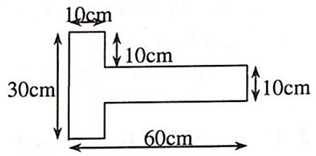
A. Không nằm trên trục đối xứng.

B. Nằm trên trục đối xứng, cách đáy 36,25cm.

C. Nằm trên trục đối xứng, cách đáy 16,5cm.

D. Nằm trên trục đối xứng, cách đáy 40,25cm.

Lời giải:

Đáp án: B

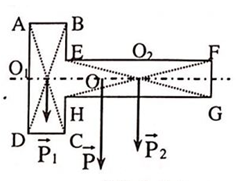
Ta chia bản mỏng ra thành hai phần ABCD và EFGH, mỗi phần có dạng hình chữ nhật. Trọng tâm của các phần này nằm tại O₁, O₂ (giao điểm các đường chéo của hình chữ nhật). Gọi trọng tâm của bản là O, O sẽ là điểm đặt của hợp các trọng lực P₁→ , P₁→ của hai phần hình chữ nhật.

Theo qui tắc hợp lực song song cùng chiều :

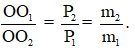
Vì bản đồng chất nên khối lượng tỉ lệ với diện tích :

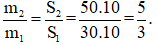
Đồng thời: O₁O₂ = OO₁ + OO₂ = = 30cm.

Từ các phương trình trên, ta suy ra: OO₁ = 18,75cm; OO₂ = 11,25cm.

Vậy trọng tâm O nằm trên trục đối xứng, cách đáy: 11,25 + 25 = 36,25cm.

Bài 64: Có 5 quả cầu nhỏ trọng lượng P, 2P, 3P, 4P, 5P gắn lần lượt trên một thanh, khoảng cách giữa hai quả cầu cạnh nhau là l, bỏ qua khối lượng của thanh. Tìm vị trí trọng tâm của hệ.

A. Cách quả cầu P một đoạn 8l/3

B. Cách quả cầu P một đoạn 10l/3

C. Cách quả cầu P một đoạn 5l/2

D. Cách quả cầu P một đoạn 11l/2

Lời giải:

Đáp án: A

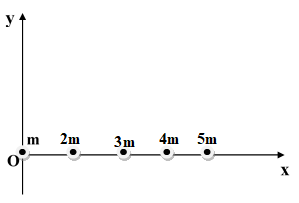
Áp dụng phương pháp tọa độ và sử dụng công thức tính tọa độ khối tâm của hệ vật ta được :

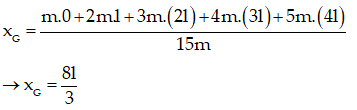
Bài 65: Cho một thanh gỗ hình hộp chữ nhật như hình vẽ có khối lượng 50 kg với AD = 80cm; AB = 40cm. Xác định lực F→ tối thiểu để làm quay khúc gỗ quanh cạnh đi qua D. Lấy g=10m/s²

A. 300N    B. 250N    C. 400N    D. 550N

Lời giải:

Đáp án: B

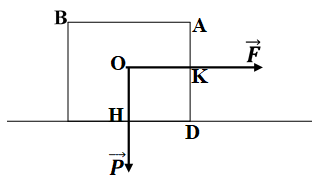
Ta có: P = m.g = 500N

Theo điều kiện cân bằng của Momen lực

→ F.DK = P.HD

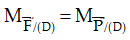
Với HD = AB/2 = 20cm; KD = AO/2 = 40cm

    → F.0,4 = 500.0,2 → F = 250 N

Bài 66: Thanh AB có khối lượng m = 15kg, đầu A tựa trên sàn nhám, đầu B nối với tường bằng dây BC nằm ngang, góc α = 60^o . Độ lớn lực ma sát tác dụng lên thanh AB.

A. 25 N    B. 21√3 N    C. 25√3 N    D. 30 N

Lời giải:

Đáp án: C

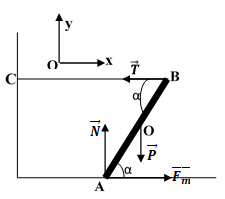
Ta có: P = m.g = 150 N

Theo điều kiện cân bằng của vật rắn quay quanh trục A:

    M_T=M_P ⇒ T.d_T = P.d_P

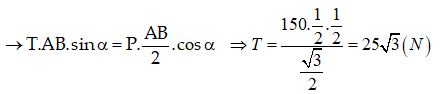
Chọn hệ quy chiếu Oxy như hình vẽ.

Theo điều kiện cân bằng của vật rắn

P→ + N→ + F_ms→ + T→ = 0→ (1)

Chiếu (1) lên Ox: F_ms - T = 0 ⇒ F_ms = 25√3 (N)

Bài 67: Thanh AB được đặt như hình vẽ có đầu A tựa trên sàn, đầu B được treo bởi dây BC. Biết BC = AB = a. Xác định điều kiện của giá trị hệ số ma sát giữa AB và sàn để AB cân bằng.

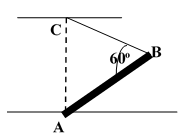
A. k < 0,54    B. k = 0,54    C. k < 0,68    D. k > 0,58

Lời giải:

Đáp án: D

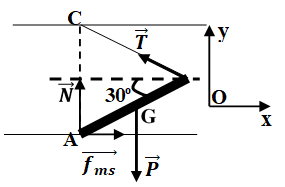
Theo điều kiện cân bằng của vật rắn đối với trục quay ở A:

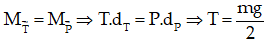
Theo điều kiện cân bằng vật rắn khi chịu tác dụng của các lực :

P→ + N→ + F_ms→ + T→ = 0→ (*)

Chon hệ trục Oxy như hình vẽ:

Tam giác CAB đều.

Chiếu (*) lên Ox: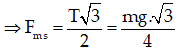

Chiếu (*) lên Oy: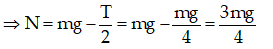

Để thanh cân bằng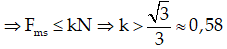

Bài 68: Cho một thang có khối lượng m = 20kg được dựa vào tường trơn nhẵn dưới góc nghiêng α. Hệ số ma sát giữa thang và sàn là k = 0,6.Tìm các giá trị của α để thang đứng yên không trượt trên sàn.

A. α > 40^o    B. α < 40^o    C. α = 40^o    D. α = 50^o

Lời giải:

Đáp án: A

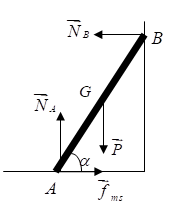
Trọng lượng của thanh: P = mg = 200N

Theo điều kiện cân bằng Momen: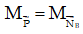

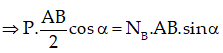
Theo điều kiện cân bằng lực: P→ + N_A→ + N_B→ + F_ms→ = 0→

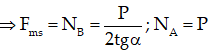
Để thang đứng yên không trượt trên sàn thì F_ms < k.N_A.

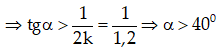
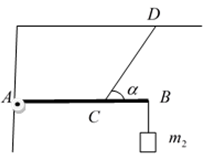
Bài 69: Thanh AB khối lượng m1 = 10kg, chiều dài l = 3m gắn vào tường bởi bản lề A. Đầu B của thanh treo vật nặng m2 = 5kg. Thanh được giữ cân bằng nằm ngang nhờ dây treo CD; góc α = 45^o. Tìm lực căng và phản lực tác dụng lên thanh AB biết AC = 2m.

A. T = 150√2 (N) và N = 150 (N)

B. T = 150√2 (N) và N = 250 (N)

C. T = 150√3 (N) và N = 250 (N)

D. T = 150√3 (N) và N = 250 (N)

Lời giải:

Đáp án: A

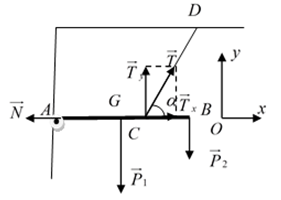
Ta có P₁ = m₁.g = 100N; P₂ = m₂.g = 50N

Theo điều kiện cân bằng của một vật rắn quay quanh một trục cố định:

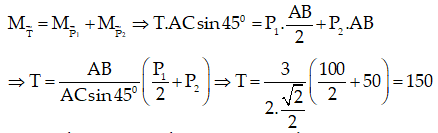
Theo điều kiện cân bằng lực của vật rắn:

P₁→ + P₂→ + T→ + N→ = 0→

Chọn hệ quy chiếu Oxy như hình vẽ.

Chiếu theo Ox ta có: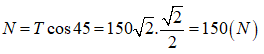

Bài 70: Thanh AB có khối lượng m = 15kg, đầu A tựa trên sàn nhám, đầu B nối với tường bằng dây BC nằm ngang, góc α = 60^o. Cho hệ số ma sát giữa AB và sàn là . Tìm các giá trị α để thanh có thể cân bằng. Biết dây BC luôn nằm ngang. Lấy g = 10m/s².

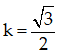
A. α = 20^o     B. α = 25^o    C. α ≥ 30^o     D. α < 25^o

Lời giải:

Đáp án: C

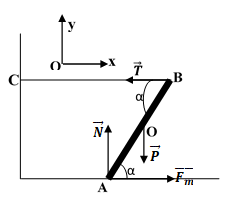
Ta có: P = m.g = 150 N

Theo điều kiện cân bằng của vật rắn quay quanh trục A:

M_T = M_P ⇒ T.d_T = P.d_P

→ T.AB.sinα =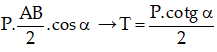

Chọn hệ quy chiếu Oxy như hình vẽ.

Theo điều kiện cân bằng của vật rắn

P→ + N→ + F_ms→ + T→ = 0→ (1)

Chiếu (1) lên Ox và Oy ta được: F_ms = T, N = P

Lúc này F_ms→ là lực ma sát nghỉ: ⇒ F_ms ≤ kN

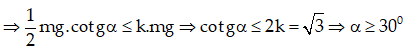
Bài 71: Cho một thang có khối lượng m = 20kg được dựa vào tường trơn nhẵn dưới góc nghiêng α. Hệ số ma sát giữa thang và sàn là k = 0,6. Một người khối lượng m’= 40kg leo lên thang khi α = 45^o. Hỏi người này lên đến vị trí O’ nào trên thang thì thang sẽ bị trượt. Biết chiều dài thang l = 2m.

A. O’ cách A một đoạn 2,9m

B. O’ cách A một đoạn 1,9m

C. O’ cách A một đoạn 2,3m

D. O’ cách A một đoạn 1,3m

Lời giải:

Đáp án: D

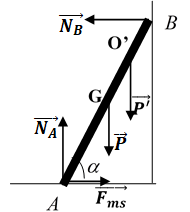
Lấy O’ là vị trí người khi thang bắt đầu trượt.

Theo điều kiện cân bằng lực: P→ + N_A→ + N_B→ + F_ms→ + P'→ = 0→

→ N_B = F_ms =kN_A; N_A = P + P' = 600N ⇒ F_ms = 360N

Xét trục quay qua A: M_NB→ = M_P→ + M_P'→

→ N_B.AB.sinα = P. .cosα + P'.AO'.cosα ⇒ AO' = 1,3 m