Các dạng bài tập Cân bằng và chuyển động của vật rắn chọn lọc, có đáp án - Vật Lí lớp 10

Các dạng bài tập Cân bằng và chuyển động của vật rắn chọn lọc, có đáp án

Với Các dạng bài tập Cân bằng và chuyển động của vật rắn chọn lọc, có đáp án Vật Lí lớp 10 tổng hợp các dạng bài tập, 140 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Cân bằng và chuyển động của vật rắn từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 10.

Tổng hợp lý thuyết Chương Cân bằng và chuyển động của vật rắn

• Lý thuyết Cân bằng của một vật chịu tác dụng của hai lực và của ba lực không song song
• Lý thuyết Cân bằng của một vật có trục quay cố định. Momen lực
• Lý thuyết Quy tắc hợp lực song song cùng chiều
• Lý thuyết Các dạng cân bằng. Cân bằng của một vật có mặt chân đế
• Lý thuyết Chuyển động tịnh tiến của vật rắn. Chuyển động quay của vật rắn quanh một trục cố định
• Lý thuyết Ngẫu lực
• Lý thuyết tổng hợp chương Cân bằng và chuyển động của vật rắn

Bài tập trắc nghiệm

• 70 câu trắc nghiệm Tĩnh học vật rắn có lời giải chi tiết (cơ bản - phần 1) Xem chi tiết
• 70 câu trắc nghiệm Tĩnh học vật rắn có lời giải chi tiết (nâng cao - phần 1) Xem chi tiết

Lý thuyết Cân bằng của một vật chịu tác dụng của hai lực và của ba lực không song song

1. Cân bằng của một vật chịu tác dụng của hai lực

    a) Điều kiện cân bằng

    Muốn cho một vật chịu tác dụng của hai lực ở trạng thái cân bằng thì hai lực đó phải cùng giá, cùng độ lớn và ngược chiều.

    F₁→ = -F₂→

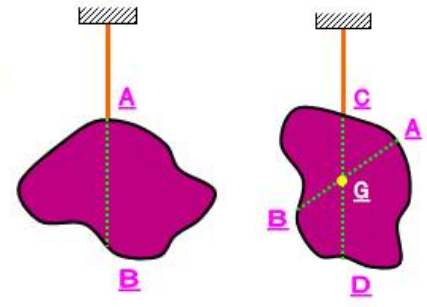
    b) Xác định trọng tâm của một vật phẳng, mỏng bằng phương pháp thực nghiệm

    Buộc dây lần lượt vào hai điểm khác nhau trên vật rồi lần lượt treo lên. Khi vật đứng yên, vẽ đường kéo dài của dây treo. Giao điểm của hai đường kéo dài này là trọng tâm của vật. Kí hiệu là G.

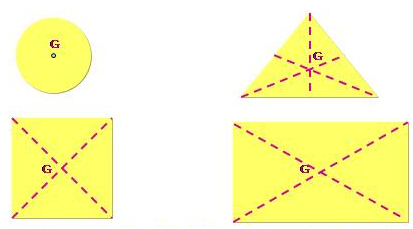
    Trọng tâm G của các vật phẳng, mỏng và có dạng hình học đối xứng nằm ở tâm đối xứng của vật.

2. Cân bằng của một vật chịu tác dụng của ba lực không song song

    a) Quy tắc tổng hợp hai lực có giá đồng quy

    Muốn tổng hợp hai lực có giá đồng quy tác dụng lên một vật rắn, trước hết ta phải trượt hai vec tơ lực đó trên giá của chúng đến điểm đồng quy, rồi áp dụng quy tắc hình bình hành để tìm hợp lực.

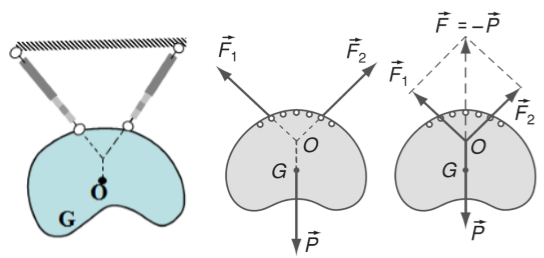
    b) Điều kiện cân bằng của một vật chịu tác dụng của ba lực không song song

    Muốn cho một vật chịu tác dụng của ba lực không song song ở trạng thái cân bằng thì:

        + Ba lực đó phải đồng phẳng và đồng quy.

        + Hợp lực của hai lực phải cân bằng với lực thứ ba.

3. Một số hiện tượng liên quan

Lý thuyết Cân bằng của một vật có trục quay cố định. Momen lực

1. Cân bằng của một vật có trục quay cô định. Momen lực

    a) Thí nghiệm

    Cho đĩa tròn có trục quay qua tâm O, trên đĩa có lỗ dùng để treo quả cân. Tác dụng vào đĩa hai lực F₁→ và F₂→ nằm trong mặt phẳng của đĩa, sao cho đĩa vẫn đứng yên

    Nếu không có lực F₂→ thì lực F₁→ làm cho đĩa quay theo chiều kim đồng hồ. Ngược lại, nếu không có lực F₁→ thì lực F₂→ làm cho đĩa quay ngược chiều kim đồng hồ. Đĩa đứng yên vì tác dụng làm quay của lực F₁→ cân bằng với tác dụng làm quay của lực F₂→.

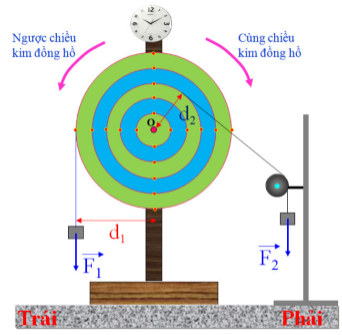
    b) Momen lực

    Momen lực đối với một trục quay là đại lượng đặc trưng cho tác dụng làm quay của lực và được đo bằng tích của lực với cánh tay đòn của nó:

    M = F.d

    Trong đó:

    F là độ lớn của lực tác dụng (N)

    d là khoảng cách từ trục quay đến giá của lực và gọi là cánh tay đòn của lực (m)

    M là momen lực (N.m)

2. Điều kiện cân bằng của một vật có trục quay cố định

    a) Quy tắc

    Muốn cho một vật có trục quay cố định ở trạng thái cân bằng thì tổng các momen lực có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các momen lực có xu hướng làm vật quay ngược chiều kim đồng hồ.

    Biểu thức: F₁.d₁ = F₂.d₂ hay M₁ = M₂

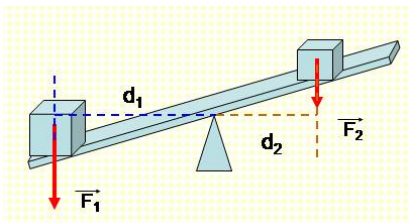
    Trong trường hợp vật chịu nhiều lực tác dụng:

    F₁.d₁ + F₂.d₂ +... = F₁’.d₁’ + F₂’.d₂’ + ...

    b) Chú ý

    Quy tắc momen còn được áp dụng cho cả trường hợp một vật không có trục quay cố định nếu như trong một tình huống cụ thể nào đó ở vật xuất hiện trục quay.

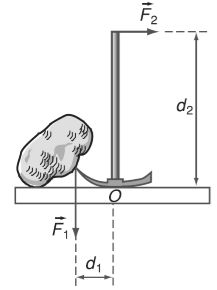
    Nếu ta thôi không tác dụng lực F₂→ vào cán, thì dưới tác dụng của lực F₁→ của tảng đá, chiếc cuốc chim sẽ quay quanh trục quay O đi qua điểm tiếp xúc của cuốc với mặt đất

Lý thuyết Quy tắc hợp lực song song cùng chiều

1. Thí nghiệm

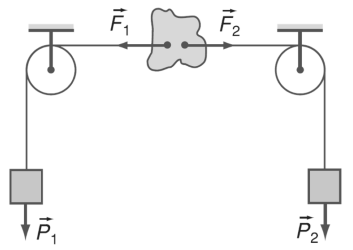
    Treo hai chùm quả cân có trọng lượng P₁ và P₂ khác nhau vào hai phía của thước:

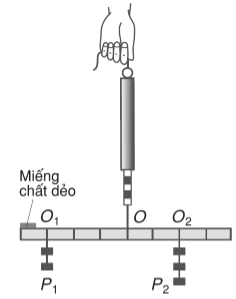
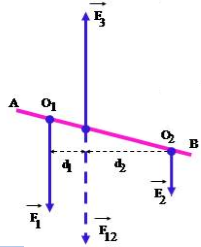
    Dùng chùm quả cân đem treo chung vào trọng tâm O của thước thì thấy thước nằm ngang và lực kế chỉ giá trị F = P₁ + P₂. Vậy trọng lực P→ = P₁→ + P₂→ đặt tại điểm O của thước là hợp lực của hai lực P₁→ và P₂→ đặt tại hai điểm O₁ và O₂.

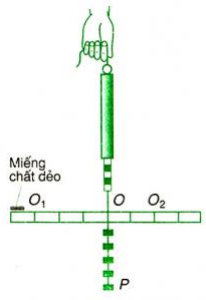
2. Quy tắc tổng hợp hai lực song song cùng chiều

    a) Quy tắc

    - Hợp lực của hai lực song song cùng chiều là một lực song song, cùng chiều và có độ lớn bằng tổng các độ lớn của hai lực ấy.

    - Giá của hợp lực chia khoảng cách giữa hai giá của hai lực song song thành những đoạn tỉ lệ nghịch với độ lớn của hai lực ấy.

    F = F₁ + F₂

    (chia trong)

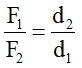
    Trong đó: d₁ là khoảng cách từ giá của hợp lực tới giá của lực F₁→

        d₂ là khoảng cách từ giá của hợp lực tới giá của lực F₂→

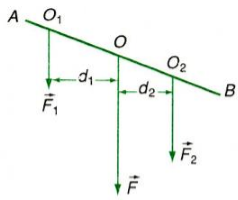
    Quy tắc trên vẫn đúng cho cả trường hợp thanh AB không vuông góc với hai lực thành phần F₁→ và F₂→.

    b) Chú ý

    - Đối với những vật đồng chất và có dạng hình học đối xứng thì trọng tâm nằm ở tâm đối xứng của vật.

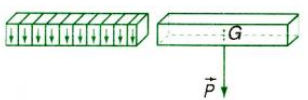
    - Có nhiều khi ta phải phân tích một lực F→ thành hai lực F₁→ và F₂→ song song và cùng chiều với lực F→. Đây là phép làm ngược lại với tổng hợp lực

3. Cân bằng của một vật chịu tác dụng của ba lực song song

    Muốn cho một vật chịu tác dụng của ba lực song song ở trạng thái cân bằng thì hợp lực của hai lực song song cùng chiều phải cùng giá, cùng độ lớn nhưng ngược chiều với lực thứ ba.

    F₁→ + F₂→ + F₃→ = 0→

4. Một số hình ảnh minh họa quy tắc hợp lực song song cùng chiều