Chương 3 (có đáp án): Vectơ trong không gian. Quan hệ vuông góc trong không gian

Haylamdo biên soạn và sưu tầm Chương 3 (có đáp án): Vectơ trong không gian. Quan hệ vuông góc trong không gian Hình học 11 đầy đủ các mức độ giúp học sinh ôn luyện trắc nghiệm từ đó đạt điểm cao trong bài thi Toán 11.

Trắc nghiệm Vectơ trong không gian có đáp án

Câu 1: Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho PA→ = mPD→ và QB→ = mQC→, với m khác 1. Vecto MP→ bằng:

A. MP→ = mQC→

B. MN→ = mPD→

C. MA→ = mPD→

D. MN→ = mQC→

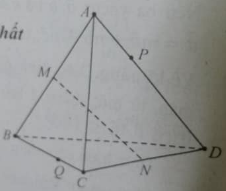
Bài tập trắc nghiệm Hình học 11 có đáp án | Trắc nghiệm Toán 11

Hiển thị đáp án

Đáp án: C

Phần dẫn ví dụ 1 là một câu chưa hoàn chỉnh, người làm chắc nghiệm phải lựa chọn một trong bốn phương án đưa ra để được một khẳng định đúng.

Có thể loại các phương án A, B và D vì các cặp ba vecto (MP→,MB→,và QC→), (MP→,MN→,PD→) và (MP→,MN→ và QC→) đều không đồng phẳng.

Phương án C đúng vì : MP→ = MA→ + AP→ = MA→ - mPD→

Câu 2: Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.

a) Vecto (MN) ⃗ cùng với hai vecto nào sau đây là ba vecto đồng phẳng?

A. MA→ và MQ→

B. MD→ và MQ→

C. AC→ và AD→

D. MP→ và CD→

b) Vecto AC→ cùng với hai vecto nào sau đây là ba vecto không đồng phẳng?

A. AB→ và AD→

B. MN→ và AD→

C. QM→ và BD→

D. QP→ và CD→

Hiển thị đáp án

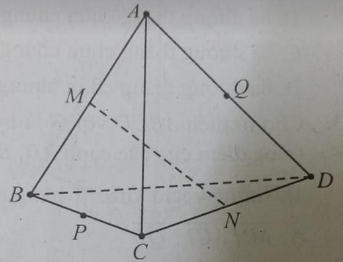
Đáp án: a - C, b - A

a) Ta có: M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC

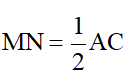
Suy ra: MN// AC và Bài tập trắc nghiệm Hình học 11 có đáp án | Trắc nghiệm Toán 11 (1)

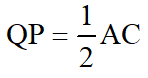
Tương tự: QP là đường trung bình của tam giác ACD nên QP // AC và Bài tập trắc nghiệm Hình học 11 có đáp án | Trắc nghiệm Toán 11 (2)

Từ (1) và (2) suy ra: tứ giác MNPQ là hình bình hành ( có các cạnh đối song song và bằng nhau

⇒ MN→ = QP→ (3)

Lại có: QP→ = 1/2 AC→ + 0. AD→ (4)

Từ (3); (4) ⇒ MN→ = 1/2 AC→ + 0. AD→

Do đó, 3 vecto MN→; AC→; AD→ đồng phẳng

b) Phương án A là đúng.

*B sai vì MN→ = 1/2 AC→ nên 3 vecto MN→; AC→ và AD→ đồng phẳng

* C sai vì QM→ = - 1/2 BD→ nên 3 vecto QM→ và BD→; AC→ đồng phẳng

*D sai vì QP→ = 1/2 AC→ nên 3 vecto QP→; AC→ và CD→ đồng phẳng

Câu 3: Cho ba vecto a→, b→, C→. Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng.

A. Một trong ba vecto đó bằng 0→.

B. Có hai trong ba vecto đó cùng phương.

C. Có một vecto không cùng hướng với hai vecto còn lại

D. Có hai trong ba vecto đó cùng hướng.

Hiển thị đáp án

Đáp án: C

Nếu hai trong ba vecto đó cùng hướng thì ba vecto đồng phẳng; nếu hai trong ba vecto đó không cùng hướng thì chưa thể kết luận được ba vecto đó đồng phẳng.

Câu 4: Ba vecto a→, b→, c→ không đồng phẳng nếu?

A. Ba đường thẳng chứa chúng không cùng một mặt phẳng.

B. Ba đường thẳng chứa chúng cùng thuộc một mặt phẳng.

C. Ba đường thẳng chứa chúng không cùng song song với một mặt phẳng.

D. Ba đường thẳng chứa chúng cùng song song với một mặt phẳng.

Hiển thị đáp án

Đáp án: C

Câu 5: Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.

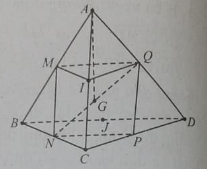
a) Những vecto khác 0→ bằng nhau là:

MN→,CI→,QP→

MI→,IQ→,QM→

MQ→,NP→, 1/2 (CB→ - CD→)

MQ→,NP→, 1/2(CD→ - CB→)

b) AB→ + AC→ + AD→ bằng:

A. 4AG→ B. 2AG→

C. AG→ D. 1/2 AG→

Hiển thị đáp án

Đáp án: a - D, b - A

a.MQ→ = NP→ = 1/2 BD→ = 1/2(CD→ - CB→);

b. AB→ + AC→ + AD→ = 2AN→ + AD→ = 4AG→

Câu 6: Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt AA'→ = a→, AB→ = b→, AC→ = c→

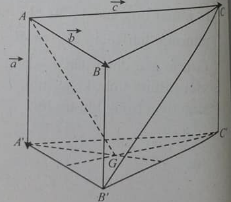
a) Vecto B'C→ bằng:

A. a→ - b→ - c→

B. c→ - a→ - b→

C. b→ - a→ - c→

D. a→ + b→ + c→

b) Vecto AG→ bằng:

A. a→ + 1/6(b→ + c→)

B. a→ + 1/4(b→ + c→)

C. a→ + 1/2(b→ + c→)

D. a→ + 1/3(b→ + c→)

Hiển thị đáp án

Đáp án: a - B, b - D

a. B'C→ = AC→ - AB'→ = AC→ - (AA'→ + AB→ ) = c→ - a→ - b→

b. AG→ = AA'→ + A'G→ = AA'→ + 1/3 (A'B'→+ A'C'→ ) = a→ + 1/3(b→ + c→)

Câu 7: Cho tứ diện ABCD và AB→ = a→,AC→ = b→,AD→ = c→. Gọi M, N, P và Q lần lượt là trung điểm của AB, BC, CD, và DA.

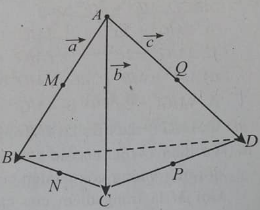
a) Vecto MQ→bằng:

A. 1/2(c→ - a→) B. 1/2(a→ - c→)

C. 1/2(c→ + a→) D. 1/4(c→ + a→)

b) Vecto MP→ bằng:

A. 1/2(c→ - a→) B. 1/2(a→ - c→)

C. 1/2(b→ + c→ - a→) D. 1/2(a→ + b→ - c→)

c) Bốn điểm M, N, P, Q cùng thuộc mặt phẳng vì:

A. MP→ = 1/2(AC→ + AD→ - AB→)

B. MP→ = 1/2 (MN→ + MQ→ )

C. MP→ = MB→ + BP→

D. MP→ = MN→ + MQ→

Hiển thị đáp án

Đáp án: a - A, b - C, c - D

a. 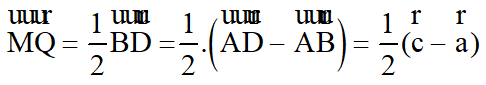Bài tập trắc nghiệm Hình học 11 có đáp án | Trắc nghiệm Toán 11

b.Loại ngay hai phương án A và B vì MP→ không đồng phẳng có vecto a→ và c→. Phương án đúng là C vì MP→ = MN→ + NP→ = 1/2(b→ + C→- a→)

c. Phương án A loại vì đẳng thức MP→ = 1/2 (AC→ + AD→ - AB→) đúng nhưng chưa chứng tỏ được bốn điểm M, N, P, Q đồng phẳng.

Phương án B loại vì đẳng thức. MP→ = 1/2(MN→+ MQ→) sai

Phương án C loại vì đẳng thức MP→ = MB→ + BP→ đúng nhưng không liên quan đến hai điểm N và Q.

Phương án D đúng vì đẳng thức MP→ = MN→ + MQ→ đúng và chứng tỏ ba vecto MP→, MN→ và MQ→ đồng phẳng.

Câu 8: Cho hình chóp tứ giác đều S. ABCD có tất cả các cạnh bằng a.

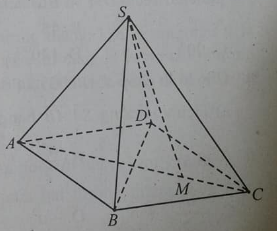
a) Số đo góc giữa BC→ và SA→ bằng:

A. 30⁰ B. 60⁰

C. 90⁰ D. 120⁰

b) Gọi M là điểm bất kì trên AC. Góc giữa MS→ và BD→ bằng 90⁰ khi M:

A. Trùng với A

B. Trùng với C

C. Là trung điểm của AC

D. Bất kì vị trí nào trên AC.

Hiển thị đáp án

Đáp án: a - B, b - C

Câu 9: 7. Cho tứ diện ABCD, E và F lần lượt là trung điểm của AB và CD, AB = 2a, CD = 2b và EF = 2c. M là một điểm bất kì.

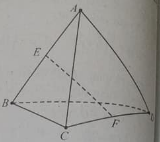
a) MA² + MB² bằng:

A. 2ME² + 2a² B. 2MF² + 2a²

C. 2ME² + 2b² D. 2MF² + 2b²

b) MC² + MD² bằng:

A. 2ME² + 2a² B. 2MF² + 2a²

C. 2ME² + 2b² D. 2MF² + 2b²

c) Gọi G là trọng tâm của tứ diện ABCD. ME² + MF² bằng:

A. 2MG² + 2a² B. 2MG² + 2b²

C. 2MG² + 2c² D. 2MG² + 2(a² + b² + c²)

d) MA² + MB² + MC² + MD² bằng:

A. 4MG² + 2a² B. 4MG² + 2b²

C. 4MG² + 2c² D. 4MG² + 2(a² + b² + c²)

Hiển thị đáp án

Đáp án: a - A, b - D, c - C

a. MA² = (ME→ + EA→ )² = ME² + EA² + 2ME→.EA→

MB² = (ME→ + EB→ )² = ME² + EB² + 2ME→.EB→

Suy ra: MA² + MB² = 2ME² + 2a² (do EA→ + EB→ = 0→)

b. Tương tự MC² + MD² = 2MF² + 2b²

c. Tương tự ME² + MF² = 2MG² + 2c²

d. MA² + MB² + MC² + MD² = 2ME² + 2MF² + 2a² + 2b² = 4MG² + 2(a² + b² + c²)

Câu 10: Tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và đều có độ dài là l. Gọi M là trung điểm của các cạnh AB. Góc giữa hai vecto OM→ và BC→ bằng:

A. 0⁰ B. 45⁰

C. 90⁰ D. 120⁰

Hiển thị đáp án

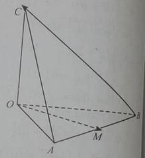
Đáp án: D

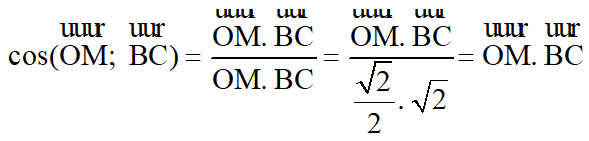
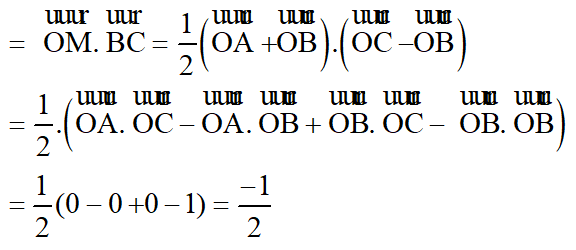
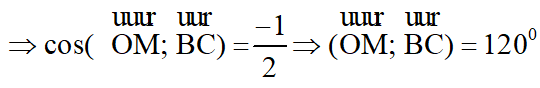
Trắc nghiệm Hai đường thẳng vuông góc với nhau có đáp án

Câu 1: Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng AC và C’D’ bằng:

A. 0⁰ B. 45⁰

C. 60⁰ D. 90⁰

Hiển thị đáp án

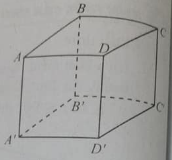
Đáp án: B

Vì CD // C’D’ nên góc giữa AC và C’D’ bằng góc giữa AC và CD – bằng góc ACD

Vì ABCD là hình vuông nên tam giác ACD vuông cân tại D

⇒ ACD = 45⁰

Câu 2: Khẳng định nào sau đây đúng?

A. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau.

B. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.

C. Hai đường thẳng cùng song song với đường thẳng thú ba thì song song với nhau.

D. Hai đường thẳng cùng song song với đường thẳng thứ ba thì vuông góc với nhau.

Hiển thị đáp án

Đáp án: C

Phần dẫn ví dụ 2 là câu hỏi. phương án A và B sai vì hai đường thẳng cùng vuông góc với đường thẳng thứ ba có thể cắt nhau hoặc chéo nhau.

Phương án C đúng vì hai đường thẳng cùng song song với đường thẳng thứ ba thì phương của chúng song song với nhau.

Phương án D sai vì hai đường thẳng cùng song song với đường thẳng thứ ba thì có thể song song hoặc trùng nhau.

Câu 3: Cho tứ diện ABCD có AB = AC = AD; góc BAC = góc BAD = 60⁰. Hãy chứng mình AB ⊥ CD.

Một bạn chứng mình qua các bước sau:

Bước 1. CD→ = AC→ - AD→

Bước 2. AB→.CD→ = AB→.(AC→ - AD→)

Bước 3. AB→.AC→ - AB→.AD→ = |AB→|.|AD→ |.cos⁡60⁰ - |AB→|.|AD→|.cos⁡60⁰ = 0〗

Bước 4. Suy ra AB ⊥ CD

Theo em. Lời giải trên sai từ :

A. bước 1 B. bước 2

C. bước 3 D. bước 4

Hiển thị đáp án

Đáp án: A

Câu dẫn là một lời giải của một bài toán cho trước, học sinh cần hiểu để có thể phê phán được lời giải bị sai từ bước nào. Phương án đúng là A.

Câu 4: Cho vecto n→ ≠ 0→ và hai vecto a→ và b→ không cùng phương. Nếu vecto n→ vuông góc với cả hai vecto a→ và b→ thì n→, a→ và b→:

A. đồng phẳng

B. không đồng phẳng

C. có thể đồng phẳng

D. có thể không đồng phẳng

Hiển thị đáp án

Đáp án: B

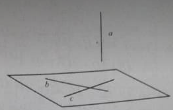
Phương án A và C sai vì có thể xảy ra trường hợp như hình vẽ sau

Giả sử phương án B cũng sai, tức là ba vecto n→, a→ và b→ đồng phẳng. Khi đó vì n→ ⊥ a→ và n→ ⊥ b→ nên giá của a→ và b→ song song. Điều này mẫu thuẫn với giả thiết hai vecto a→ và b→ không cùng phương. Vì vậy phương án B đúng.

Câu 5: Cho ba vecto n→, a→, b→ bất kì đều khác với vecto 0→. Nếu vecto n→ vuông góc với cả hai vecto a→ và b→ thì n→, a→ và b→:

A. đồng phẳng

B. không đồng phẳng

C. có giá vuông góc với nhau từng đôi một

D. có thể đồng phẳng

Hiển thị đáp án

Đáp án: D

Phương án A sai (hình trên)

Phương án B và C sai vì có thể sảy ra như hình sau.

Phương án D đúng vì: có thể ba vecto n→, a→ và b→ đồng phẳng hoặc không đồng phẳng như hai hình trên.

Câu 6: 3. Nếu ba vecto a→, b→, c→ cùng vuông góc với vecto n→ khác 0→ thì chúng.

A. đồng phẳng

B. không đồng phẳng

C. có thể đồng phẳng

D. có thể không đồng phẳng

Hiển thị đáp án

Đáp án: A

Phương án A đúng vì giả sử a→, b→ và c→ không đồng phẳng, khi đó tồn tại duy nhất bộ số thực (x; y; z) sao cho n→ = xa→ + yb→ + zc→

Nhân cả hai vế với vecto n→ ta có : n→.n→ = xa→.n→ + yb→.n→ + zc→.n→ = 0

⇒ n→ = 0→. Điều này trái với giả thiết.

Câu 7: Các đường thẳng cùng vuông góc với một đường thẳng thì:

A. thuộc một mặt phẳng

B. vuông góc với nhau

C. song song với một mặt phẳng

D. song song với nhau

Hiển thị đáp án

Đáp án: C

Phương án A sai vì có thể xảy ra trường hợp chúng nằm trên nhiều mặt phẳng khác nhau

Phương án B sai vì có thể xảy ra trường hợp chúng song song với nhau

Phương án D sai vì có thể xảy ra trường hợp chúng cắt nhau

Phương án C đúng vì chúng đồng phẳng

Câu 8: Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a và các góc phẳng đỉnh B đều bằng 60⁰.

a) Cặp đường thẳng nào sau đây không vuông góc với nhau?

A. B’C và AD’ B. BC’ và A’D

C. B’C và CD’ D. AC và B’D’

b) Đường thẳng B’C vuông góc với đường thẳng:

A. AC B. CD

C. BD D. A’A

Hiển thị đáp án

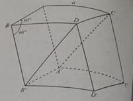
Đáp án: a - C, b - B

a. Phương án A, B và D đều sai

Phương án C đúng vì tam giác CB’D’ có ba cạnh bằng a, a√3,a√3 nên không thể vuông tại B’

b. Phương án A sai vì tam giác ACB’ có ba cạnh bằng a

Phương án C sai vì tam giác CB’D’ có ba cạnh a, a√3,a√3 nên không thể vuông tại B’

Phương án D sai vì góc giữa đường thẳng B’C và AA’ bằng 0⁰

Phương án B đúng vì:

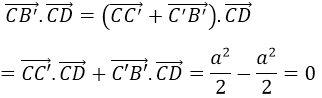
Câu 9: Cho tứ diện ABCD. Nếu AB ⊥CD, AC ⊥ BD và BC ⊥ AD thì:

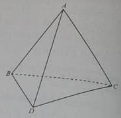
A. AB→.AC→ ≠ AC→.AD→ = AB→.AD→

B. AB→.AC→ = AC→.AD→ ≠ AB→.AD→

C. AB→.AC→ = AC→.AD→ = AB→.AD→

D. AB→.AC→ ≠ AC→.AD→ ≠ AB→.AD→

Hiển thị đáp án

Đáp án: C

Ta có: AB→.CD→ = AC→.BD→ = AD→.CB→ = 0

⇒AB→(AD→ - AC→) = AC→(AD→ - AB→ ) = AD→(AB→ - AC→) = 0

⇒AB→.AC→ = AC→.AD→ = AB→.AD→

Câu 10: Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng 60⁰. Gọi M và N là trung điểm của AB và CD

a) Góc giữa AB→ và CD→ bằng:

A. 30⁰ B. 60⁰

C. 90⁰ D. 120⁰

b) Kết luận nào sau đây sai?

A. MN vuông góc với AB

B. MN vuông góc với CD

C. MN vuông góc với AB và CD

D. MN không vuông góc với AB và CD

Hiển thị đáp án

Đáp án: a - C, b - D

AB→.CD→ = AB→(AD→ - AC→) = 0,suy ra AB ⊥ CD

b. phương án A sai vì AB→.MN→ = AB→(CN→ - CM→ ) = 0. Phương án B sai theo bài 9. Hiển nhiên phương án C sai AB→.CD→ = AB→(AD→ - AC→) = 0,suy ra AB ⊥ CD

b. phương án A sai vì AB→.MN→ = AB→(CN→ - CM→) = 0. Phương án B sai theo bài 9. Hiển nhiên phương án C sai.

Xem thêm các bài giải Bài tập trắc nghiệm Hình Học 11 khác:

❮ Bài trước Bài sau ❯