19 câu trắc nghiệm Phép đối xứng trục có đáp án (phần 1)
19 câu trắc nghiệm Phép đối xứng trục có đáp án (phần 1)
Haylamdo biên soạn và sưu tầm 19 câu trắc nghiệm Phép đối xứng trục có đáp án (phần 1) Hình học 11 đầy đủ các mức độ giúp học sinh ôn luyện trắc nghiệm từ đó đạt điểm cao trong bài thi Toán 11.

Câu 1: Cho hình vuông ABCD tâm I. gọi E, F, G, H lần lượt là trung điểm của các cạnh DA, AB, BC, CD. Phép đối xứng trục AC biến:
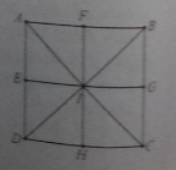
A. ∆IED thành ∆IGC B. ∆IFB thành ∆IGB
C. ∆IBG thành ∆IDH D. ∆IGC thành ∆IFA
Đáp án: C
Tìm ảnh của từng điểm qua phép đối xứng trục AC: điểm I biến thành I; B thành D; G thành H. Chọn đáp án C
Câu 2: Trong mặt phẳng Oxy cho điểm M(-1;3). Phép đối xứng trục Ox biến M thành M’ thì tọa độ M’ là:
A. M’(-1;3) B. M’(1;3)
C. M’(-1;-3) D. M’(1;-3)
Đáp án: C
(x' = x; y' = -y). Chọn đáp án C
Câu 3: Trong mặt phẳng Oxy cho đường thẳng d có phương trình : x - 2y + 4 = 0. Phép đối xứng trục Ox biến d thành d’ có phương trình:
A. x - 2y + 4 = 0
B. x + 2y + 4 = 0
C. 2x + y + 2 = 0
D. 2x - y + 4 = 0
Đáp án: B
Phép đối xứng trục Ox có
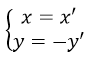
thay vào phương trình d được x'+ 2y' + 4 = 0 hay x + 2y + 4 = 0. Chọn đáp án B
Câu 4: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình:
(x - 3)2 + (y - 1)2 = 6. Phép đối xứng trục Oy biến (C) thành (C’) có phương trình
A. (x + 3)2 + (y - 1)2 = 36
B. (x + 3)2 + (y - 1)2 = 6
C.(x - 3)2 + (y + 1)2 = 36
D. (x + 3)2 + (y + 1)2 = 6
Đáp án: B
Phép đối xứng trục Oy biến tâm I(3;1) của (C) thành I’(-3;1); bán kính không thay đổi. Chọn đáp án B.
Câu 5: Trong mặt phẳng Oxy cho điểm M(2;3). Điểm M là ảnh của điểm nào trong bốn điểm sau qua phép đối xứng trục Oy?
A. A(3;2) B. B(2; -3)
C. C(3;-2) D. D(-2;3)
Đáp án: D
Câu 6: Trong các mệnh đề sau mệnh đề nào đúng?
A. Tam giác đều có vô số trục đối xứng
B. Một hình có vô số trục đối xứng thì hình đó phải là đường tròn
C. Hình gồm hai đường thẳng vuông góc có vô số trục đối xứng
D. Hình tròn có vô số trục đối xứng
Đáp án: D
Phương án A. Tam giác đều chỉ có ba trục đối xứng là ba đường cao.
Phương án B. Đường thẳng cũng có vô số trục đối xứng (là đường thẳng bất kì vuông góc với đường thẳng đã cho).
Phương án C. Hình gồm hai đường thẳng vuông góc có bốn trục đối xứng (là chính hai đường thẳng đó và hai đường phân giác của góc tạo bởi hai đường thẳng đó).
Câu 7: Trong mặt phẳng, hình vuông có mấy trục đối xứng?
A. một
B. hai
C. ba
D. bốn
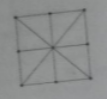
Đáp án: D
Hai đường chéo và hai đường trung bình.
Câu 8: Trong mặt phẳng, hình nào sau đây có trục đối xứng?
A. hình thang vuông
B. hình bình hành
C. hình tam giác vuông không cân
D. hình tam giác cân
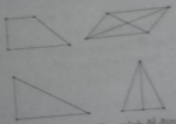
Đáp án: D
Tam giác cân có trục đối xứng là đường cao (cúng là trung trực, phân giác).
Câu 9: Trong mặt phẳng, cho hình thang cân ABCD có AD = BC. Tìm mệnh đề đúng :
A. có phép đối xứng trục biến AD→ thành BC→ nên AD→ = BC→
B. có phép đối xứng trục biến AC→ thành BD→ nên AC→ = BD→
C. có phép đối xứng trục biến AB thành CD nên AB // CD
D. có phép đối xứng trục biến DA thành CB nên DA = CB
Đáp án: D
Câu 10: Trong mặt phẳng cho hai đường thẳng a và b tạo với nhau góc 600. Có bao nhiêu phép đối xứng trục biến a thành b.
A. một B. hai
C. ba D. bốn
Đáp án: B
Hai đường phân giác của góc tạo bởi a và b.
Nhận xét: Giả thiết góc 600 chỉ để gây nhiễu

