Trắc nghiệm Toán 11 Bài 3 (có đáp án): Đường thẳng vuông góc với mặt phẳng (phần 1)
Bài tập trắc nghiệm Toán 11 Bài 3 (có đáp án): Đường thẳng vuông góc với mặt phẳng (phần 1)
Haylamdo biên soạn và sưu tầm Trắc nghiệm Toán 11 Bài 3 (có đáp án): Đường thẳng vuông góc với mặt phẳng (phần 1) phần Hình học đầy đủ các mức độ giúp học sinh ôn luyện trắc nghiệm từ đó đạt điểm cao trong bài thi Toán 11.

Bài 1: Đường thẳng a vuông góc với hai đường thẳng phân biệt trong mặt phẳng (P) thì :
A. a vuông góc với mặt phẳng (P)
B. a không vuông góc với mặt phẳng (P)
C. a không thể vuông góc với mặt phẳng (P)
D. a có thể vuông góc với mặt phẳng (P)
Đáp án: D
Phương án A sai vì có thể có trường hợp a ⊥ b ⊂ (P); a⊥c ⊂ (P); b // c
Phương án B sai vì có thể xảy ra trường hợp a ⊥ b ⊂ (P); a⊥ c ⊂ (P); b ∩ c ≠ ∅, khi đó a⊥(P).
Bài 2: Mệnh đề nào sau đây là sai?
A. nếu a // (P) và b ⊥ (P) thì b ⊥ a
B. nếu a // (P) và b ⊥ a thì b ⊥ (P)
C. nếu a ⊂ (P) và b ⊥ (P) thì b ⊥ a
D. nếu a ⊂ (P), a ⊆(P) và b ⊥ a thì b ⊥ (P)
Đáp án:
Bài 3: Mệnh đề nào sau đây là đúng?
A. hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
B. hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
C. một đường thẳng và một mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
D. các đường thẳng cùng vuông góc với một đường thẳng thì cùng thuộc một mặt phẳng.
Đáp án: B
Phương án A sai vì có thể xảy ra trường hợp hai đường thẳng đó vuông góc với nhau
Phương án C sai vì có thể xảy ra trường hợp đường thẳng thuộc mặt phẳng
Phương án D sai vì các đường thẳng đó có thể không đồng phẳng
Bài 4: Mệnh đề nào sau đây sai?
A. hai đường thẳng cùng vuông góc môt mặt phẳng thì song song hoặc trùng nhau.
B. hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
C. hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
D. hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Đáp án: C
Bài 5: Các đường thẳng cùng vuông góc với một đường thẳng thì:
A. thuộc một mặt phẳng
B. vuông góc với nhau
C. song song với một mặt phẳng
D. song song với nhau
Đáp án: C
Bài 6: Cho hình lập phương ABCD. A’B’C’D’.
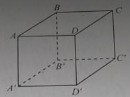
a) AA’ vuông góc với mặt phẳng.
A. (CDD’C’) B. (BCD)
C. (BCC’B’) D. (A’BD)
b) AC vuông góc với mặt phẳng.
A. (CDD’C’) B. (A’B’C’D’)
C. (BDD’B’) D. (A’BD)
c) Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:
A. trung điểm của BD
B. trung điểm của A’B
C. trung điểm của A’D
D. tâm O của tam giác BDA’
Đáp án: a - B, b - C, c - D
b. Phương án A sai vì AC không vuông góc với CD ⊂ (CDD’C’)
Phương án B sai vì AC // (A’B’C’D’)
Phương án C đúng vì AC ⊥ BD , AC⊥ BB’ và BD, BB’ ⊂ (BDD’B’)
c. Phương án D đúng vì BD ⊥ (AMA') bởi BD ⊥ AM và BD ⊥ A’M ⇒ BD ⊥ AO
BA’ ⊥ (AND) do BA’ ⊥ DN và A’B ⊥ AN ⇒ A’B ⊥ AO
AO ⊥ (A’BD) ⇒ O là hình chiếu của A trên (A’BD).
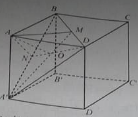
Bài 7: Cho hình chóp S.ABCD, đáy là hình thoi tâm O và SA = SC, SB = SD
a) Lời giải nào sau đây là đúng?
Chứng minh rằng SO ⊥ (ABCD)

D. Cả ba phương án trên đều sai.
b) Đường thẳng AC vuông góc với mặt phẳng
A. (SAC) B. (SBD)
C. (ABCD) D. (SDC)
Đáp án: a - C, b - B
a) Phương án A sai vì DO không phải là hình chiếu của SO trên (ABCD). Phương án B sai vì SA và SC, SB và SD bằng nhau từng đôi một nên hình chóp S.ABCD không phải là hình chóp đều. Phương án C đúng.
b) Loại phương án A và C vì AC thuộc (SAC) và (ABCD). Phương án B đúng vì: AC ⊥ BD (hai đường chéo hình thoi) và AC ⊥ SO(vì tam giác SAC cân tại S), nên AC ⊥ (SBD).
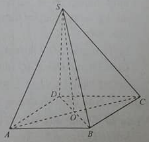
Bài 8: Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD.
a) Đường thẳng DB không vuông góc với đường thẳng nào sau đây?
A. AC B. SA C. SB D. SC
b) Đường thẳng BC vuông góc với đường thẳng
A. SA B. SB C. SC D. SO
Đáp án: a - C, b - D
a) Dễ thấy BD ⊥ AC (tính chất hình thoi), BD ⊥ SC và BD ⊥ SA và DB ⊥ (SAC). Vì vậy phương án đúng là C.
b) Phương án đúng là D: BC ⊥ SO vì SO ⊥ (ABCD) (xem ví dụ 1)
Bài 9: Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ (ABCD)

a) Tam giác SBC là:
A. Tam giác thường B. Tam giác cân
C. Tam giác đều D. Tam giác vuông
b) Tam giác SOD là:
A. Tam giác thường B. Tam giác cân
C. Tam giác đều D. Tam giác vuông
Đáp án: a - D, b - D
a) Tam giác SBC là tam giác vuông tại B vì : AB là hình chiếu của SB trên (ABCD), mà BC ⊥ AB (do ABCD là hình vuông) ⇒ BC ⊥ SB (theo định lí ba đường vuông góc) ⇒ tam giác SBC là tam giác vuông
b) Tam giác SDO là tam giác vuông tại O vì AO là hình chiếu của SO trên (ABCD) , mà DO ⊥ AO (do ABCD là hình vuông) ⇒ DO ⊥ SO (theo định lí ba đường vuông góc) ⇒ tam giác SOD là tam giác vuông.
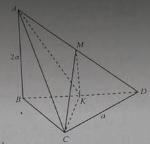
Bài 10: Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
a) Gọi M là trung điểm của AD và K là trung điểm của BD
Góc giữa CM với mặt phẳng (BCD) là:

b) Tang của góc giữa CM với mặt phẳng (BCD) bằng:
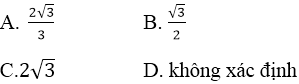
c) Tang của góc giữa AC với mặt phẳng (ABD) bằng:

d) Tang của góc giữa AK với mặt phẳng (ABC) bằng:
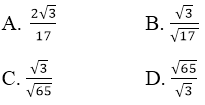
Đáp án: a - C, b - A, c - C, d - C
a) Loại phương án A và B vì BC và CD không phải là hình chiếu của CM trên (BCD)
Phương án C đúng vì :
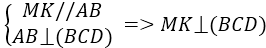
⇒ CK là hình chiếu của CM trên mặt phẳng (BCD)
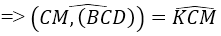
Góc giữa CM và mặt phẳng (BCD) là góc KCM.
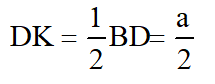
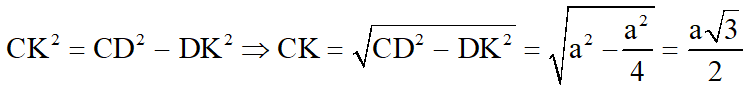
Phương án đúng là A vì :
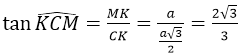
Góc giữa AC với mặt phẳng (ABD) là góc KAC vì CK ⊥ (ABD) nên AK là hình chiếu của AC trên mặt phẳng (ABD).
Phương án C đúng vì :
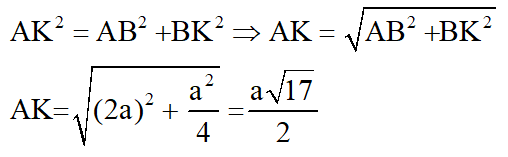
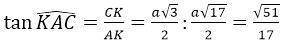
d) Để xác định giữa AK với mặt phẳng (ABC) từ K dựng KN ⊥ BC.
p>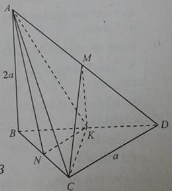
⇒ KN ⊥ (ABC) vì KN vuông góc với BC và AB
Gọi P là trung điểm của BC, tam giác BCD đều nên DP vuông góc BC.
Lại có: KN ⊥ BC nên DP // KN
Vì K là trung điểm của BD nên N là trung điểm của BP
Ta có:
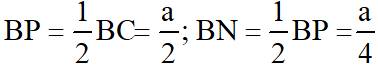
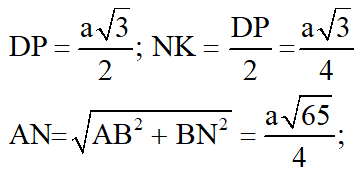
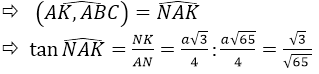
Vậy phương án đúng là C.

