Trắc nghiệm Toán 11 Bài 3 (có đáp án): Đường thẳng vuông góc với mặt phẳng (phần 2)
Bài tập trắc nghiệm Toán 11 Bài 3 (có đáp án): Đường thẳng vuông góc với mặt phẳng (phần 2)
Haylamdo biên soạn và sưu tầm Trắc nghiệm Toán 11 Bài 3 (có đáp án): Đường thẳng vuông góc với mặt phẳng (phần 2) phần Hình học đầy đủ các mức độ giúp học sinh ôn luyện trắc nghiệm từ đó đạt điểm cao trong bài thi Toán 11.

Bài 11: Cho hình tứ diện ABCD, có AB, BC, CD đôi một vuông góc với nhau và AB = a, BC = b, CD = c.

a) Khẳng định nào sau đây là đúng?
A. AB ⊥ (ACD) B. BC ⊥ (ACD)
C. CD ⊥ (ABC) D. AD ⊥ (BCD)
b) Độ dài AD bằng
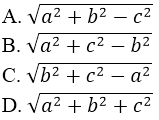
c) Điểm cách đều 4 điểm A, B, C, D là:
A. trung điểm của AB
B. trung điểm của BC
C. trung điểm của AD
D. trung điểm của CD
Đáp án: a - C, b - D, c - C
a. Phương án A sai vì chỉ có AB ⊥ CD
Phương án B sai vì chỉ có BC ⊥ CD
Phương án C đúng vì:
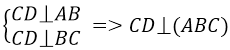
Phương án D sai vì AD không vuông góc với đường thẳng nào thuộc mặt phẳng (BCD)
b. Ta có
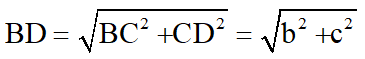
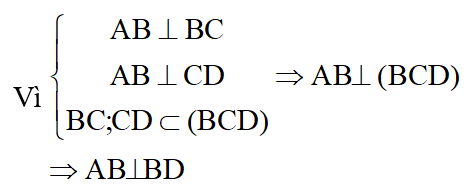
Tam giác ABD vuông tại B nên 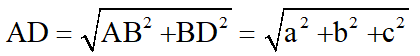
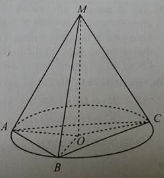
c. xem hình bên.
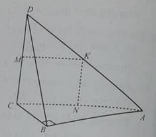
CD ⊥ (ABC) vì CD ⊥ BC và AB ⊥ CD. AB ⊥ (BCD) vì AB ⊥ BC và AB ⊥ CD
Phương án A sai vì tam giác ABC không vuông góc tại C nên trung điểm của AB không cách đều ba điểm A, B, C
Phương án B sai vì tam giác ABC không vuông góc tại A nên trung điểm của AB không cách đều ba điểm A, B, C
Phương án C đúng vì: tam giác ACD vuông góc tại C nên trung điểm K của AD cách đều ba điểm A, C, D; tam giác ABD vuông góc tại B nên trung điểm K của AD cách đều ba điểm A, B, D
Phương án D sai vì tam giác CBD không vuông góc tại B nên trung điểm của Cd không cách đuề ba điểm B, C, D
Bài 12: Cho hình tứ diện OABC có OA, OB, OC đôi một vuông góc. Gọi I là hình chiếu của điểm O trên mặt phẳng (ABC).
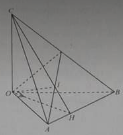
a) Tam giác ABC là:
A. Tam giác vuông
B. Tam giác có một góc tù
C. Tam giác cân đỉnh A
D. Tam giác có ba góc nhọn
b) Điểm I là:
A. Trọng tâm của tam giác ABC
B. Trực tâm của tam giác ABC
C. Tâm của đường tròn ngoại tiếp tam giác ABC
D. Tâm của đường tròn nội tiếp tam giác ABC.
Đáp án: a - D, b - B
a. Giả sử tam giác ABC vuông tại A. khi đó B có hai đường thẳng BO và BA cùng vuông góc với mặt phẳng (OCA). Điều này vô lí, do đó tam giác ABC không thể là tam giác vuông. Từ O hạ OH ⊥ AB ⇒ CH ⊥ AB (theo định lí ba đường vuông góc). Vì điểm H nằm giữa hai điểm A và B nên tam giác ABC không thể có góc tù. Suy ra ABC có ba góc nhọn
b. giả sử AI và CI cắt CB tại K và H
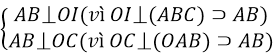
⇒ AB ⊥ (OCH) ⇒ AB ⊥ CH
Chứng mình tương tự ta cũng có CB ⊥ AK ⇒I là trực tâm của tam giác ABC
Bài 13: Cho hình chop S.ABC có ABC là tam giác đều cạnh a và SA= SB = SC = b. gọi G là trọng tâm tam giác ABC. Một mặt phẳng (P) đi qua A và vuông góc với SC, cắt SC tại K.
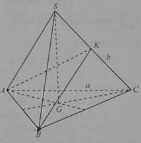
a) Độ dài của SG là:
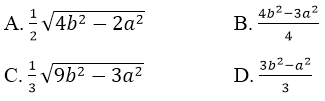
b) Điều kiện để điểm K nằm giữa hai điểm S và C là:
A. a = b B. a = b√2
C. a ≥ b√2 D. a < b√2
c) Nếu a = b√2 thì thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (P) là:
A. tam giác SAB
B. tam giác KAB
C. tam giác CAB
D. tam giác SBC
Đáp án: a - C, b - D, c - A
a. Giả sử H là chân đường vuông góc hạ tự S xuống mặt phẳng (ABC). Khi đó, do SA = SB = SC ⇒ HA = HB = HC ⇒ H là tâm đường tròn ngoại tiếp tam giác ABC ⇒ H ≡ G. Vì tam giác ABC đều cạnh a nên:
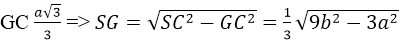
b. điểm K sẽ nằm giữa hai điểm S và C khi
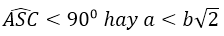
c. Nếu a = b√2 thì Sa, SB, SC đôi một vuông góc ⇒ SC ⊥ (SAB)
Do đó (P) ≡ (SAB), hay thiết diện của hình chóp S.ABC khi cắt bởi mặt phẳng (P) là tam giác SAB
Bài 14: Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC.
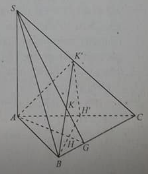
a) Mặt phẳng (BKH) vuông góc với đường thẳng:
A. SC B. AC
C. AH D. AB
b) Đường thẳng HK vuông góc với mặt phẳng.
A. (ABC) B. (BK’H’)
C. (ASG) D. (SBC)
Đáp án: a - A, b - D
a. Vì K là trực tâm của ∆SBC nên BK ⊥ SC (1)
Vì H là trực tâm của ∆ABC nên BH ⊥ AC. Mặt khác BH ⊥ SA ⊥ (ABC) nên BH ⊥ (SAC) ⇒ BH ⊥ SC (2)
b. Từ (1) va (2) suy ra SC ⊥ (BHK). Vì BC ⊥ (ASG) ⇒ BC ⊥ HK và SC ⊥ (BHK) ⇒ SC ⊥ HK. Suy ra HK ⊥ (SBC)
Bài 15: Cho hình tứ diện OABC có OA, OB, OC đôi một vuông góc. Nếu I là hình chiếu của điểm O trên mặt phẳng (ABC) thì I là:
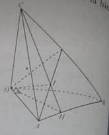
A. trọng tâm của tam giác ABC.
B. trực tâm của tam giác ABC.
C. tâm của đường tròn ngoại tiếp tam giác ABC.
D. tâm của đường tròn nội tiếp tam giác ABC.
Đáp án: B
Giả sử AI và CI cắt CB và AB tại K và H
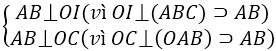
⇒ AB ⊥ (OCH) ⇒ AB ⊥ CH
Chứng minh tương tự ta cũng có CB ⊥ AK ⇒ I là trực tâm của tam giác ABC
Bài 16: Cho hình tứ diện ABCD có ba cạnh AB. BC, CD đôi một vuông góc.
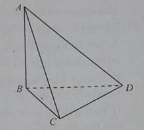
a) Đường thẳng AB vuông góc với :
A. (BCD) B. (ACD) C. (ABC)
D. (CDI) với I là trung điểm của AB
b) Đường vuông góc chung của AB và CD là:
A. AC B. BC
C. AD D. BD
Đáp án: a - A, b - B
a. AB ⊥ (BCD) vì AB ⊥ BC và AB ⊥ CD
b. Phương án A sai vì AB và Cd không vuông góc với nhau
Phương án B đúng vì BC⊥ AB (do AB ⊥ (BCD); BC ⊥ CD(giả thiết)
Bài 17: Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng 600. Gọi M, N là trung điểm của AB và CD.
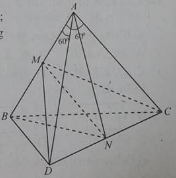
Đường thẳng CD vuông góc với mặt phẳng
A. (ABD) B. (ABC)
C. (ABN) D. (CMD)
Đáp án: C
Phương án A sai vì nếu CD ⊥ (ABD) thì CD ⊥ AD. Nhưng tam giác ACD cân tại A nên CD không thể vuông góc với AD
Phương án B sai vì tương tự như trên thì CD không thể vuông góc với AC
Phương án C đúng vì CD ⊥ AN (AN là đường trung tuyến của tam giác cân CAD tại A) và CD ⊥ MN ⇒ CD ⊥ (ABN)
Phương án D sai vì CD không vuông góc với MD do chứng minh trên.
Bài 18: Cho một điểm S có hình chiếu H trên mặt phẳng (P).
a) Với điểm M bất kì trong (P) ta có:
A. SM lớn hơn SH
B. SM không nhỏ hơn SH
C. SM không lớn hơn SH
D. SM nhỏ hơn SH
b) Với hai điểm M và N trong (P) sao cho SM ≤SN, ta có:
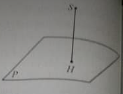
A. điểm M bao giờ cũng khác điểm N
B. ba điểm M, N, H có thể trùng nhau
C. hai điểm M và N luôn khác điểm H
D. ba điểm M, N, H không thể trùng nhau.
Đáp án: a - B, b -B
a. Phương án A sai vì khi M trùng với H thì SM = SH
Phương án B đúng vì khi M trùng với H thì SM = SH; khi M ≠ H thì SM > SH
Phương án C, D sai vì không bao giờ xảy ra trường hợp SM < SH
Bài 19: . Mặt phẳng trung trực của đoạn thẳng AB:
A. luôn vuông góc với AB tại một điểm bất kì trên AB
B. luôn cách đều hai đầu mút A và B
C. luôn vuông góc với AB tại trung điểm của AB
D. luôn song song với AB.
Đáp án: C
Bài 20: Tập hợp các điểm cách đều ba đỉnh của tam giác ABC là:
A. tâm đường tròn ngoại tiếp tam giác ABC.
B. tâm đường tròn nội tiếp tam giác ABC.
C. đường thẳng vuông góc với mặt phẳng (ABC) và đi qua tâm đường tròn ngoại tiếp tam giác ABC.
D. đường thẳng vuông góc với mặt phẳng (ABC) và đi qua tâm đường tròn nội tiếp tam giác ABC.
Đáp án: C
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, MO là đường thẳng vuông góc với mặt phẳng (ABC) tại O.
Ta có: OA, OB, OC lần lượt là hình chiếu của các đường xiên MA, MB, MC. Vì OA = OB = OC
⇒ MA = MB = MC. Vậy đường thẳng MO là tập hợp các điểm cách đều ba đỉnh A, B, C của tam giác ABC.