30 câu trắc nghiệm tổng ôn Toán 11 cả năm Hình học chọn lọc, có lời giải chi tiết (phần 1)
30 câu trắc nghiệm tổng ôn Toán 11 cả năm Hình học chọn lọc, có lời giải chi tiết (phần 1)
Haylamdo biên soạn và sưu tầm 30 câu trắc nghiệm tổng ôn Toán 11 cả năm Hình học chọn lọc, có lời giải chi tiết (phần 1) đầy đủ các mức độ giúp học sinh ôn luyện trắc nghiệm từ đó đạt điểm cao trong bài thi Toán 11.

Câu 1: Câu nào sau đây đúng?
A. Qua hai đường thẳng bất kì xác định một mặt phẳng duy nhất
B. Qua một đường thẳng và một điểm xác định một mặt phẳng duy nhất.
C. Qua hai đường thẳng cắt nhau xác định một mặt phẳng duy nhất.
D. Qua hai đường thẳng không có điểm chung xác định một mặt phẳng
Đáp án: C
1. Có thể sửa lại các câu sai thành các câu đúng như sau:
A. Qua hai đường thẳng bất kì không xác định một mặt phẳng duy nhất
B. Qua một đường thẳng và một điểm nằm ngoài nó xác định một mặt phẳng duy nhất.
C. Qua hai đường thẳng cắt nhau xác định một mặt phẳng duy nhất
D. Qua hai đường thẳng không có điểm chung chưa kết luận được chúng xác định mặt phẳng duy nhất
Câu 2: Câu nào sau đây đúng?
A. Nếu ba điểm cùng thuộc hai mặt phẳng thì chúng thẳng hàng
B. Nếu hai mặt phẳng có một điểm chung thì chúng cắt nhau theo giao tuyến đi qua điểm chung ấy.
C. Nếu hai đường thẳng không có điểm chung thì chúng không cùng nằm trông một mặt phẳng
D. Nếu hai đường thẳng phân biệt có một điểm chung thì chúng cùng nằm trong một mặt phẳng.
Đáp án: D
2. Có thể sửa lại các câu sau thành các câu đúng như sau:
A. Nếu ba điểm cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng
B. Hai mặt phẳng phân biệt có một điểm chung thì chúng cắt nhau theo giao tuyến đi qua điểm chung ấy
C. Nếu hai đường thẳng không có điểm chung thì chưa kết luận được chúng không cùng nằm trong một mặt phẳng
D. Nếu hai đường thẳng có một điểm chung thì chúng cùng nằm trong một mặt phẳng
Câu 3: Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì:
A. Ba đường thẳng đó đồng quy
B. Ba đường thẳng đó tạo thành một tam giác
C. Ba đường thẳng đó trùng nhau
D. Không có ba đường thẳng như vây.
Đáp án: A
Câu 4: Câu nào sau đây là đúng?
A. Hình tứ diện là một hình chóp có đáy là tứ giác
B. Hình tứ diện là một hình chóp có đáy là tam giác
C. Thiết diện của hình tứ diện là một tứ giác
D. Thiết diện cảu hình tứ diện là một tam giác
Đáp án: B
Câu 5: Câu nào sau đây là đúng?
A. Hai đường thẳng không có điểm chung thì song song với nhau
B. Hai mặt phẳng đi qua hai đường thẳng song song thì song song với nhau
C. Hai đường thẳng nằm trên hai mặt phẳng song song thì song song với nhau
D. Cả ba mệnh đề trên đều sai
Đáp án: D
5. Có thể sủa lại các câu sai thành các câu đúng như sau:
A. Hai đường thẳng cùng nằm trên một mặt phẳng và không có điểm chung thì song song với nhau
B. Hai mặt phẳng đi qua hai đường thẳng song song thì có thể song song với nhau hoặc cắt nhau
C. Hai đường thẳng nằm trên hai mặt phẳng song song thì có thể song song với nhau hoặc chéo nhau
Câu 6: Câu nào sau đây là đúng?
A. a // b và b ⊂ (P) thì a // (P)
B. a // b , b ⊂ (P); a ⊂ (Q), (Q) ∩ (P) = c thì c // a
C. (Q) ∩ (P) = a, (R) ∩(P) = b và a // b thì (P) // (Q)
D. a ⊂(P), b ⊂(Q) và a chéo b thì (P) // (Q)
Đáp án: B
Có thể sửa lại các câu sai thành các câu đúng như sau.
A. Sửa lại: a//b , b ⊂ (P) và a ⊄ (P) thi a// (P)
B. a//b, b⊂ (P), a ⊄ (P); (Q) qua a và (Q) ∩ (P) = c thì c//a
C. (Q) ∩ (P) = a, (R) ∩ (P) = b và a//b thì có thể (R) // (Q) hoặc (R) cắt (Q)
D. a ⊂ (P); b ⊂ (Q) và a chéo b thì có thể (P) // (Q) hoặc (P) cắt (Q)
Câu 7: Cho hình chóp S.ABCD, các cặp đường thẳng nào sau đây chéo nhau?
A. AB và CD B. AD và BC
C. SA và BD D. AC và BD
Đáp án: C
Phương án C: SA chéo BD.
Câu 8: Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
B. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song với nhau
C. Hai đường thẳng và một mặt phẳng cùng vuông góc với một mặt phẳng khác thì song song với nhau.
D. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau.
Đáp án: D
Có thể sửa lại các câu sai thahf các câu đúng như sau.
A. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì có thể song song, chéo nhau hoặc vuông góc với nhau
B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau
C. Một đường thẳng và một mặt phẳng – không chứa đường thẳng đó – cùng vuông góc với một mặt phẳng khác thì song song với nhau
D. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau
Câu 9: Tìm mệnh đề đúng trong các mệnh đề sau?
A. Đường thẳng a vuông góc với đường thẳng b nằm trong mặt phẳng (P) không chứa a thì a vuông góc với (P)
B. Mặt phẳng (P) vuông góc với đường thẳng a nằm trong mặt phẳng (Q) thì (P) vuông góc với (Q)
C. Đường thẳng a vuông góc với hai đường thẳng b,c nằm trong mặt phẳng (P) thì a vuông góc với (P)
D. Đường thẳng a song song với đường thẳng b nằm trong mặt phẳng (P) thì a song song với mặt phẳng (P)
Giả thiết chung cho câu 10, 11, 12. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Tìm mệnh đề đúng?
Đáp án: B
9. Có thể sửa lại các câu sai thành các câu đúng như sau:
A. Đường thẳng a vuông góc với hai đường thẳng b, c cắt nhau nằm trong mặt phẳng (P) thì a vuông góc với (P)
B. Mặt phẳng (P) vuông góc với đường thẳng a nằm trong mặt phẳng (Q) thì (P) vuông góc với (Q)
C. Đường thẳng a vuông góc với hai đường thẳng b, c cắt nhau nằm trong mặt phẳng (P) thì a vuông góc với (P)
D. Đường thẳng a song song với đường thẳng b nằm trong mặt phẳng (P) không chứa a thì a song song với mặt phẳng (P)
Câu 10: Giao tuyến của hai mặt phẳng (MNP) và (ACD) là:
A. MP B. NQ C. MQ D. AP
Đáp án: C
(MNP) ∩ (ACD) = (MNQ) ∩ (ACD) = MQ.

Câu 11: Đường thẳng MP không chéo với đường thẳng nào sau đây?
A. AB B. CD C. NP D. BC
Đáp án: C
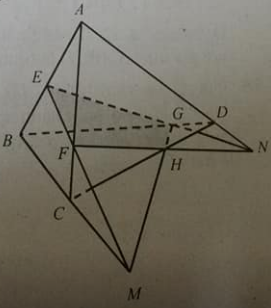
Câu 12: Tỉ số QD/QC bằng:
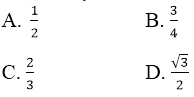
Đáp án: A
Áp dụng định lí Mê-nê-la-uýt:
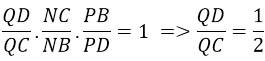
Câu 13: Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên các cạnh AB, AC, BD sao cho EF cắt BC tại M, EG cắt AD tại N. tìm mệnh đề sai trong các mệnh đề sau đây?
A. (EFG) ∩ (ACD) = FN
B. (EFG)∩ (BCD) = MG
C. đường thẳng CD, MG, FN đồng quy
D. bốn điểm M, G, F, G không cùng nằm trên một mặt phẳng.
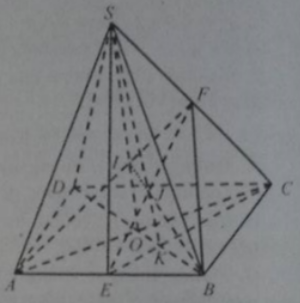
Giả thiết chung cho các câu 14, 15, 16: cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của AB và SC; I, J lần lượt là giao điểm của AF và EF với mặt phẳng (SBD).
Đáp án: D
Trong mặt phẳng (ACD) : FN cắt CD tại H ⇒ H ∈ (EFG) và H ∈ (BCD) ⇒ H ∈ MG là giao tuyến của (EFG) và (BCD) hay FN, MG, CD đồng quy tại H ⇒ M, N, F, G đồng phẳng
Câu 14: Tỉ số IA/IF bằng:
A. 1 B. 2 C. 3 D. 4
Đáp án: B
Trong mặt phẳng (SAC) : AF ∩S O = I là trọng tâm tam giác SBD ⇒ IA/IF=2
Câu 15: Tỉ số EJ/IF bằng
A. 2 B. 1 C. 2/3 D. 3/4
Đáp án: B
Trong mặt phẳng (ABCD) : BD ∩ EC = K
Trong mặt phẳng (SEC) : EF ∩ SK = J. Áp dụng định lí Me-nê-la-uýt vào tam giác EFC ta được : EJ/JF = 1