Trắc nghiệm Toán 11 Bài 4 (có đáp án): Phép đối xứng tâm (phần 2)
Bài tập trắc nghiệm Toán 11 Bài 4 (có đáp án): Phép đối xứng tâm (phần 2)
Haylamdo biên soạn và sưu tầm Trắc nghiệm Toán 11 Bài 4 (có đáp án): Phép đối xứng tâm (phần 2) phần Hình học đầy đủ các mức độ giúp học sinh ôn luyện trắc nghiệm từ đó đạt điểm cao trong bài thi Toán 11.

Bài 11: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình:
(x - 3)2 + (y - 1)2 = 4. Phép đối xứng có tâm O là gốc tọa độ biến (C) thành (C’) có phương trình:
A. x2 + y2 - 6x - 2y - 6 = 0
B. x2 + y2 - 2x - 6y + 6 = 0
C. x2 + y2 + 6x - 2y - 6 = 0
D. x2 + y2 + 6x + 2y + 6 = 0
Đáp án: D
Đường tròn (C) có tâm I(3; 1) và bán kính R = 2.
Phép đối xứng tâm O(0; 0) biến tâm I(3; 1) của (C) thành tâm I’(-3; -1) của đường tròn (C’), bán kính R = 2 không đổi.
Phương trình (C’) là (x + 3)2 + (y + 1)2 = 4 hay x2 + y2 + 6x + 2y + 6 = 0
Bài 12: Trong mặt phẳng Oxy cho parabol (P) có phương trình y = x2 - 3x + 1. Phép đối xứng tâm O(0;0) biến (P) thành (P’) có phương trình:
A. y = x2 + 3x - 1
B. y = -x2 + 3x + 1
C. y = -x2 - 3x - 1
D. y = -x2 - 3x + 1
Đáp án: C
Phép đối xứng tâm O biến M(x; y) thuộc (P) thành điểm M’(x’; y’) thuộc (P’).
Trong đó;
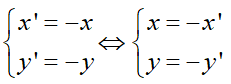
thay vào phương trình (P) ta được
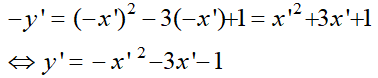
hay y = -x2 - 3x - 1
Bài 13: Trong mặt phẳng Oxy cho parabol (P) có phương trình: y = x2 - 3x + 1. Phép đối xứng tâm I(4; -3) biến P thành (P’) có phương trình:
A. y = -x2 + 13x - 47
B. y = x2 - 13x + 47
C. y = -x2 - 13x - 47
D. y = -x2 - 13x + 47
Đáp án: A
Phép đối xứng tâm I biến M(x; y) thành M’(x’; y’) thì:
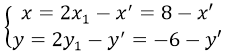
Thay vào phương trình (P) ta được:
-6 - y' = (8 - x')2 - 3(8 - x') + 1 ⇒ -y' = x'2 - 13x' + 47 hay
y = -x2 + 13x - 47
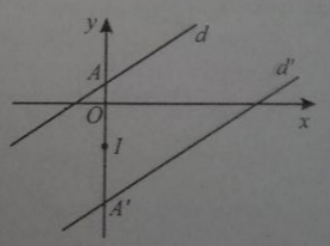
Bài 14: Trong mặt phẳng Oxy cho đường thẳng d có phương trình x - 2y + 20 = 0; đường thẳng d’ có phương trình x - 2y - 8 = 0. Tìm tọa độ điểm I sao cho phép đối xứng tâm I biến d thành d’ đồng thời biến trục Oy thành chính nó.
A. I(-2;0) B. I(8;0)
C. I(-3/2;0) D. I(0; -3/2)
Đáp án: D
Dễ thấy d // d’, ta có d ∩ Oy = A(0; 1); d’ ∩ Oy = A’(0; -4). Phép đối xứng tâm I biến Oy thành Oy thì I thuộc trục Oy; biến d thành d’ thì I là trung điểm của AA’ ⇒ I(0; -3/2).
Bài 15: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 6x + 5y - 7 = 0; điểm I(2;-1). Phép đối xứng tâm I biến d thành d’ có phương trình:
A. 6x - 5y - 7 = 0 B. 6x + 5y - 7 = 0
C. 6x - 5y + 7 = 0 D. 6x + 5y + 7 = 0
Đáp án: B
Tâm đối xứng I thuộc d thì phép đối xứng tâm I biến d thành chính nó.
Nhận xét: lưu ý kiểm tra xem tâm có thuộc d không, cũng như với phép tịnh tiến thì kiểm tra xem vecto tịnh tiến có cùng phương với vecto chỉ phương của d không.
Bài 16: Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình : 3x - 5y + 7 = 0; đường thẳng d’ có phương trình 3x - 5y + 12 = 0. Một lần đối xứng của (H) là:
A. (1;2) B. (-4;0) C. (0;19/2) D. (19/2;0)
Đáp án: C
Hai đường thẳng d và d’ song song. Điểm A(1; 2) thuộc d và điểm B(-4; 0) thuộc d’ nên bị loại
Tính khoảng cách từ C tới hai đường thẳng d, d’
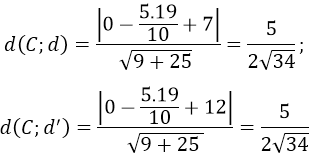
⇒ d(C;d)=d(C;d^')=> C là tâm đối xứng
Nhận xét: nếu I là tâm đối xứng của hình gồm hai đường thẳng song song thì I cách đều hai đường thẳng song song đó.
Bài 17: Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình 3x - 5y + 7 = 0 và đường thẳng d’ có phưng trình:
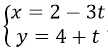
Tâm đối xứng của (H) là:
A. I(-7/2;7/2) B. I(7;-7)
C. I(7/2;7/2) D. I(7;7)
Đáp án: C
Đường thẳng d có vecto chỉ phương u→(5;3); Đường thẳng d’ có vecto chỉ phương v→(-3;1) nên d không song song với d’. Tâm đối xứng của hình (H) chính là giao điểm của d và d’:
Gọi I là giao điểm của d và d’.
Điểm I thuộc d’ nên tọa độ I(2- 3t; 4+ t)
Lại có, I thuộc d nên thay tọa độ điểm I vào phương trình đường thẳng d ta được:
3(2 - 3t) - 5(4 + t) + 7 = 0 ⇒ -14t = 7
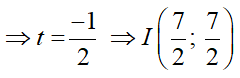
Bài 18: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x - 2)2 + (y + 4)2 = 9 và đường tròn (C’) có phương trình (x - 3)2 + (y + 3)2 = 9. Phép đối xứng tâm K biến (C) thành (C’). tọa độ của K là:
A. K(2; -4) B. K(3; -3)
C. K(-7/2;5/2) D. K(5/2; -7/2)
Đáp án: D
Đường tròn (C) có tâm I(2; -4), bán kính R= 3
Đường tròn (C’) có tâm J( 3; -3) và bán kính R’ = 3
Vì R= R’ nên tồn tại phép đối xứng tâm: biến đường tròn (C) thành (C’).
Khi đó; tâm đối xứng K là trung điểm IJ.
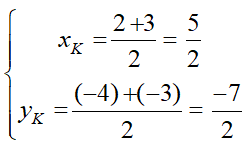
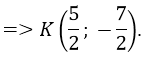
Bài 19: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x2 + y2 + 2x - 6y + 6 = 0; điểm I(1;2). Phép đối xứng tâm I biến (C) thành (C’) có phương trình:
A. x2 + y2 - 6x - 2y + 6 = 0
B. x2 + y2 - 2x - 6y + 6 = 0
C. x2 + y2 + 6x - 2y - 6 = 0
D. x2 + y2 - 6x + 2y + 6 = 0
Đáp án: A
Phép đối xứng tâm I(1; 2) biến M(x; y) thành M’(x’; y’) thì:
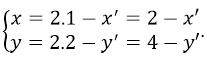
Thay vào phương trình (C) ta được:
(2 - x' )2 + (4 - y')2 + 2(2 - x' ) - 6(4 - y' ) + 6 = 0
⇒ x'2 + y'2 - 6x' - 2y' + 6 = 0 hay x2 + y2 - 6x - 2y + 6 - 0

